Зубьев конического колеса

Схема зубострогания. Обработка зубьев конических колес на зубострогальных станках, работающих по методу обката, теоретически основана на представлении о производящем колесе - воображаемом плоском кониче­ском колесе, с которым обкатывается в процессе обработки заготовка. Ха­рактерным для плоского колеса является величина угла при вершине на­чального конуса 2ф₀ = 180° (рис. 12.1, а), благодаря которой дополни­тельный конус превращается в цилиндр с осью zz и образующей аЬ. При развертке цилиндра на плоскость зубья колеса образуют прямобочную зубчатую рейку.

Процесс формообразования зубьев на заготовке можно представить се­бе так (рис. 12.2). Предположим, что заготовка выполнена из идеального пластичного материала. Если ее перекатывать без скольжения по стально­му коническому плоскому (производящему) колесу, то зубья последнего на поверхности заготовки формируют впадины. После одного оборота заго­товки вокруг своей оси образуется зубчатый венец, зубья которого будут очерчены по окгоидальному профилю, который мало отличается от приня­того эвольвентного профиля и вполне удовлетворяет практическим требо­ваниям. То же самое произойдет и в случае, если, не перекатывая заготов­ку, заставить вместе с ней вращаться производящее колесо (как показано на рисунке). Вращение заготовки и производящего колеса должно быть ки­нематически связано и происходить без скольжения по начальным кону­сам. В данном случае, имея в виду плоское коническое колесо (2ф₀ = 180°), начальный конус нарезаемого колеса должен катиться но начальной пло­скости хх (см. рис. 12.1, а).

Оставим на производящем колесе 1 только два зуба (рис. 12.2). Сооб­щим заготовке 2 и производящему колесу вращение в направлении стре­лок. После того как заготовка перекатится через два зуба, реверсируем вращение и возвращаем оба колеса в исходное положение. В результате описанных перемещений два зуба производящего колеса образуют на заго­товке две впадины: зуб 5 - впадину 4, зуб 6 - впадину 3. Таким образом, будет получен первый зуб на заготовке.

Повернем заготовку в исходном положении вокруг своей оси против часовой стрелки на угол, соответствующий шагу зацепления, и повторим весь цикл предыдущих обкаточных движений. Тогда зуб 5 образует на за­готовке новую впадину (на рисунке не показана), а зуб 6 будет входить в контакт с уже имеющейся впадиной 4. В результате второго цикла дви­жений получим второй зуб на заготовке, и так далее, до тех пор, пока не будут образованы все зубья. Итак, процесс формообразования зубьев со­вершается в результате ряда чередующихся циклов движений. Каждый же цикл состоит из обкаточного движения производящего колеса заготовки, в процессе которого зубья колеса внедряются в материал заготовки, обра­зуя впадины; реверсирования и обкаточного движения в обратном направ­лении; движения деления в конце обратного хода, когда заготовка повора­чивается на один зуб. Зубья 5 и 6 производящего колеса заменяют двумя резцами 7 и 8.

Резцы попеременно совершают прямолинейное возвратно-поступатель­ное движение в радиальном направлении. Режущие кромки аЬ я а₁Ь₁ в своем поступательном движении в плоскостях abed и а₁b₁с₁d₁ образуют впадину производящего колеса. Поэтому, если наряду с прямолинейным, перемещением сообщить резцам вращение вместе с производящим коле­сом вокруг точки О, то в обкаточном движении они, врезаясь в заготовку, выстрагивают впадины. Режущие кромки аЬ и а ₁ Ь ₁ в своем относительном движении огибают боковые поверхности зуба нарезаемого колеса. По­скольку толщина резцов меньше толщины зуба производящего колеса, впадины 3 и 4 при первом контакте с резцами не будут иметь полной ши­рины.

Таким образом, при обработке зубьев прямозубых конических колес необходимо осуществлять следующие движения: главное движение - пря­молинейное возвратно-поступательное перемещение резцов; движение об­катки - вращение заготовки и производящего колеса (резцов); движение деления - поворот заготовки в конце обратного хода. Чтобы строгать впадины, нужно вершины резцов перемещать в радиальном_направлении вдоль образующей уу дна впадины (см. рис. 12.1, а). Однако для создания более простой конструкции станка в практике допу­скают отступление: образующую уу дна впадины совмещают с пло­скостью хх, перпендикулярной к оси вращения производящего колеса, и вершины

резцов перемещаются в этой плоскости (см. рис.

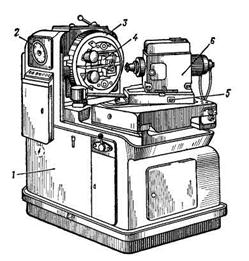
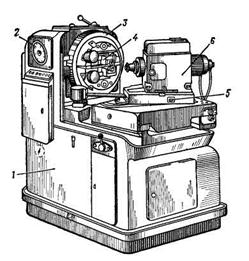
Рис.12.3.Зубострогальный

полуавтомат мод.5Т23В для 12.1, б). В связи с этим угол 2φ₀ при вершине

обработки прямозубых начального конуса производящего колеса бу­дет

конических колес меньше 180°. Из схемы следует, что

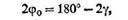
где γ - угол ножки нарезаемого колеса. Если через z обозначить число зубьев нарезаемого колеса, а через z _н - число зубьев производящего колеса, то на основании известных зави­-

симостей, для конических зубчатых колес можно написать

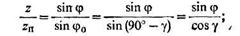
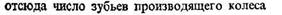
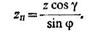
Так как угол у мал, то cosy ≈1. Поэтому можно принять

z_n = z / sinφ.

Дата добавления: 2014-01-04