Основные понятия. Оптимизация - поиск наилучшего решения с учетом ограничений

Оптимизация - поиск наилучшего решения с учетом ограничений.

Для оптимизации ищется целевая функция. Эта функция конструируется искусственно на основе уравнений, описывающих объект оптимизации. Целевая функция обычно имеет много аргументов: φ=f (х1, х2,..., х n).

Чтобы найти оптимальное значение, перебирают значение аргументов хi пошагово до тех пор, пока значение φ станет удовлетворять условиям оптимума. Даже количество аргументов не более трех, "тупой" перебор может потребить очень много времени.

Поэтому разработаны десятки методов оптимизации:

- первый строгий математический метод предложил в 1840г. венгерский математик Коши - МСС - метод скорейшего спуска. При формулировании задач оптимизации обычно стараются ее свести к поиску минимума. МСС относится к классу градиентных методов.

Градиент - вектор, указывающий на направление максимального возрастания функции.

Антиградиент - вектор, указывающий на направление максимального убывания функции. Чтобы повернуть вектор на 180╟, достаточно изменить все знаки у градиентов на противоположные (т.е. х (-1)).

Для иллюстрации поиска экстремума в процессе оптимизации функций двух переменных используют линии равного уровня (ЛРУ). Если задаться постоянным значением φ и так подбирать значения хi чтобы значение φ было равным заданному значению, то геометрическое место точек φ составит линию равного уровня.

В зависимости от целевой функции линий равного уровня могут характеризоваться следующими географическими понятиями:

Долина - когда соседние линии равного уровня изменяется очень слабо в широком диапазоне аргументов.

Возвышенность - когда соседние линии равного уровня представляют собой замкнутые линии и значение φ возрастает от внешних линий к внутренним.

Впадина - когда соседние линии равного уровня представляют собой замкнутые линии, и значение φ убывает от внешних линий к внутренним.

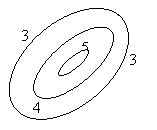
Седловина - локальный минимум, в центре которого векторы указывают на возрастание функции, но вскоре направление вектора резко изменяется вверх или вниз.

МСС - простейший метод оптимизации, пригодный для сложных систем. Работа метода хорошо иллюстрируется с помощью линий равного уровня (ЛРУ).

Порядок поиска оптимума:

- выбирается исходная точка в виде значений параметров целевой функции:

φ=f (х1, х2,..., х n).

- ищется градиент;

- движемся в направлении антиградиента с заданным шагом;

- на каждом шаге проверяем выполнение условия движения, оно такое: φi < φi-1 (текущее значение φ должно быть меньше предыдущего).

- если условие движения нарушается, то процесс останавливается, иначе, движение продолжается;

- при нарушении условий движения уточняется одномерный минимум и ищется новый градиент;

- условие останова:

а) значение φ меньше заданного;

б) разность значений соседних φ меньше заданной;

в) количество шагов превышает допустимое.

- если после останова минимума не удовлетворяет требованиям, то либо ищется другая исходная точка и процесс повторяется, либо выбирается другой метод оптимизации.

Дата добавления: 2014-01-04