
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Постановка задачи. Транспортные задачи линейного программирования
|
|
|
|
Транспортные задачи линейного программирования
Под термином «транспортные задачи» понимается широкий круг задач не только транспортного характера. Общим для них является, как правило, распределение ресурсов, находящихся у т производителей (поставщиков), по п потребителям этих ресурсов.
На автомобильном транспорте наиболее часто встречаются следующие задачи, относящиеся к транспортным:
• прикрепление потребителей ресурса к производителям;
• привязка пунктов отправления к пунктам назначения;
• взаимная привязка грузопотоков прямого и обратного направлений;
• отдельные задачи оптимальной загрузки промышленного оборудования;
• оптимальное распределение объемов выпуска промышленной
продукции между заводами-изготовителями и др.
Рассмотрим экономико-математическую модель прикрепления пунктов отправления к пунктам назначения. Имеются т пунктов отправления груза и объемы отправления по каждому пункту а1, а2,…аm. Известна потребность в грузах b1, b2,…bn по каждому из п пунктов назначения. Задана матрица стоимостей доставки по каждому варианту cij, i = 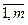 , j =
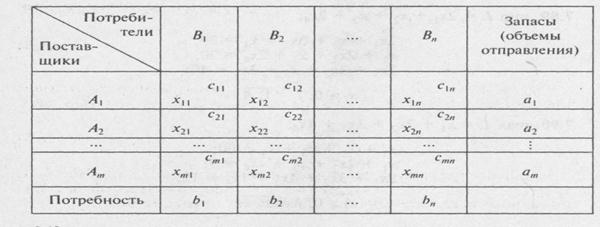
, j =  . Необходимо рассчитать оптимальный план перевозок, т. е. определить, сколько груза должно быть отправлено из каждого i–го пункта отправления (от поставщика) в каждый j-й пункт назначения (до потребителя) xij с минимальными транспортными издержками. В общем виде исходные данные представлены в табл. 7.1.
. Необходимо рассчитать оптимальный план перевозок, т. е. определить, сколько груза должно быть отправлено из каждого i–го пункта отправления (от поставщика) в каждый j-й пункт назначения (до потребителя) xij с минимальными транспортными издержками. В общем виде исходные данные представлены в табл. 7.1.
Таблица 7.1 – Исходные данные
Транспортная задача называется закрытой, если суммарный объем отправляемых грузов 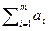 равен суммарному объему потребности в этих грузах по пунктам назначения
равен суммарному объему потребности в этих грузах по пунктам назначения  :
:
 (1)
(1)
Если такого равенства нет (потребности выше запасов или наоборот), задачу называют открытой, т. е.:
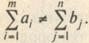 (2)
(2)
Для написания модели необходимо все условия (ограничения) и целевую функцию представить в виде математических уравнений. Все грузы из i-х пунктов должны быть отправлены, т. е.:
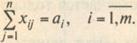 (3)
(3)
Все j-е пункты (потребители) должны быть обеспечены грузами в плановом объеме:
 (4)
(4)
Суммарные объемы отправления должны равняться суммарным объемам назначения:
 (5)
(5)
Должно выполняться условие неотрицательности переменных: xij ≥0,, i = 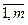 , j =
, j =  . Перевозки необходимо осуществить с минимальными транспортными издержками (функция цели):
. Перевозки необходимо осуществить с минимальными транспортными издержками (функция цели):
 (6)
(6)
В модели (3) — (6) вместо матрицы стоимостей перевозок (Cij) могут задаваться матрицы расстояний. В таком случае в качестве целевой функции рассматривается минимум суммарной транспортной работы. Как видно из выражения (5), уравнение баланса является обязательным условием решения транспортной задачи. Поэтому, когда в исходных условиях дана открытая задача, то ее необходимо привести к закрытой форме. В случае если
o потребности по пунктам назначения превышают запасы пунктов
отправления, то вводится фиктивный поставщик с недостающим
объемом отправления;
o запасы поставщиков превышают потребности потребителей, то
вводится фиктивный потребитель с необходимым объемом потребления.
Варианты, связывающие фиктивные пункты с реальными, имеют нулевые оценки. После введения фиктивных пунктов задача решается как закрытая.
Транспортным задачам присущи следующие особенности:
o распределению подлежат однородные ресурсы;
o условия задачи описываются только уравнениями;
o все переменные выражаются в одинаковых единицах измерения;
o во всех уравнениях коэффициенты при неизвестных равны единице;
o каждая неизвестная встречается только в двух уравнениях системы ограничений.
Транспортные задачи могут решаться симплекс-методом. Однако перечисленные особенности позволяют для транспортных задач применять более простые методы решения.
|
|
|
|
Дата добавления: 2014-01-04; Просмотров: 782; Нарушение авторских прав?; Мы поможем в написании вашей работы!