Метод линейного программирования для нахождения оптимальных стратегий в играх двух лиц с нулевой суммой

Пусть игра m×n не имеет оптимального решения непосредст­венно в чистых стратегиях, т. е. отсутствует седловая точка (α ≠ β). Оптимальное решение необходимо искать в области смешанных стратегий. Предположим, что все m стратегий игрока А полезные. Определим вероятности их применения в смешанной оптимальной стратегии. Обозначим эти вероятности через , а цену иг­ры — через М. Оптимальная смешанная стратегия игрока А опреде­ляется из условия (38):

Пусть

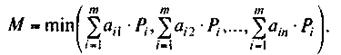(41)

Поскольку при оптимальной стратегии средний выигрыш не меньше М при любой стратегии противника, то справедлива систе­ма n неравенств:

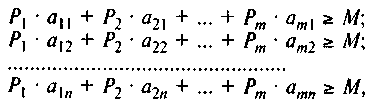(42)

или

(43)

Тогда задача отыскания оптимальной смешанной стратегии игрока А может быть сформулирована в виде задачи линейного программирования.

Для этого необходимо максимизировать Z=M при ограничениях

(44)

Введём неизвестные: .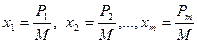

Для исключения возможности деления на ноль, увеличим цену игры на положительное число С. Для этого достаточно ко всем элементам матрицы ||а_ij|| прибавить одно и тоже положительное число С, при этом все элементы а_ij сделать положительными. Эта операция не меняет искомых оптимальных стратегий.

Поскольку

Разделим левую и правую части неравенств (43) и (44) на М, получим:

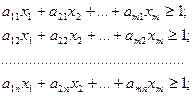(45)

x₁+x₂+…+x_m= (46)

В силу того что max M=min 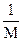=min{x₁+x₂+…+x_m },

задача принимает вид

Z= x₁+x₂+…+x_m, (47)

при ограничениях . (48)

Для игрока В оптимальная стратегия определяется из условия:

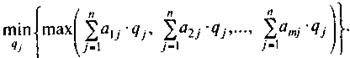
при ограничениях

q₁+q₂+…+q_n=1. (49)

Эта задача записывается как симметричная двойственная задача линейного программирования к задаче игрока А:

максимизировать

L=Y₁+Y₂+…+Y_n

при ограничениях

,

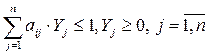где L=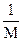, Y_j=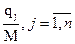

Задачи игроков А и В решают обычным симплекс-методом.

Дата добавления: 2014-01-04