
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Два целых числа и называются сравнимыми по модулю, если при делении на это число они дают одинаковые остатки
|
|
|
|
Обозначается: 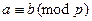 . Например,
. Например,  ,
,  . Так вот, функцию
. Так вот, функцию  можно рассматривать, как сложение по модулю 2. Действительно, сумма остатков от деления чисел 0 и 1 на число 2 равна 1, а сумма остатков от деления чисел 0 и 0, либо 1 и 1 на 2 равна 0.
можно рассматривать, как сложение по модулю 2. Действительно, сумма остатков от деления чисел 0 и 1 на число 2 равна 1, а сумма остатков от деления чисел 0 и 0, либо 1 и 1 на 2 равна 0.
Функция 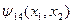 называется импликацией или логическим следованием. Обозначается:
называется импликацией или логическим следованием. Обозначается:  .
.
Функция  называется эквивалентностью или равнозначностью. Она равна 1, если значения переменных одинаковы и 0, если они различны. Обозначается:
называется эквивалентностью или равнозначностью. Она равна 1, если значения переменных одинаковы и 0, если они различны. Обозначается: 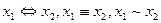 .
.
Есть ещё две функции двух переменных, имеющие специальные названия. Функция  называется стрелкой Пирса и обозначается
называется стрелкой Пирса и обозначается  . Функция
. Функция 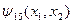 называется штрихом Шеффера и обозначается
называется штрихом Шеффера и обозначается 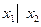 . Остальные функции специальных названий не имеют и, как можно показать, легко выражаются через перечисленные выше функции.
. Остальные функции специальных названий не имеют и, как можно показать, легко выражаются через перечисленные выше функции.
В функциях  и
и 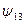 переменная
переменная 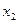 фиктивна. Из таблицы 3 видно, что
фиктивна. Из таблицы 3 видно, что  , а
, а  . Аналогично, в функциях
. Аналогично, в функциях 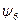 и
и 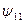 переменная
переменная 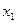 фиктивна:
фиктивна:  , а
, а 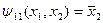 .
.
Доказано, что с ростом числа переменных 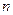 доля функций, имеющих фиктивные переменные, убывает и стремится к нулю.
доля функций, имеющих фиктивные переменные, убывает и стремится к нулю.
- Суперпозиции и формулы.
Ранее было введено определение суперпозиции функций, согласно которому суперпозицией нескольких функций называлась новая функция, полученная с помощью подстановок данных функцией друг в друга и переименования переменных. Выражение, описывающее эту суперпозицию, называли формулой. Поскольку понятие суперпозиции является очень важным в алгебре логики, рассмотрим его более подробно.
Пусть дано множество (конечное или бесконечное) исходных функций 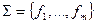 . Символы переменных
. Символы переменных 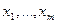 , содержащихся в данных функциях, будем считать формулами глубины 0.
, содержащихся в данных функциях, будем считать формулами глубины 0.
Определение. Говорят, что формула 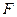 имеет глубину
имеет глубину  , если она имеет вид
, если она имеет вид 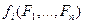 , где
, где 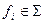 , а
, а 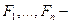 формулы, максимальная из глубин которых равна
формулы, максимальная из глубин которых равна  . При этом
. При этом 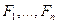 называются подформулами формулы
называются подформулами формулы 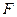 , а
, а 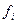 называется внешней, или главной операцией формулы
называется внешней, или главной операцией формулы 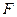 .
.
Соответственно, формулы 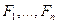 также могут иметь подформулы, которые являются в этом случае и подформулами формулы
также могут иметь подформулы, которые являются в этом случае и подформулами формулы 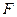 . Например, выражение
. Например, выражение 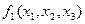 в наших обозначениях – это формула глубины 1. Выражение
в наших обозначениях – это формула глубины 1. Выражение 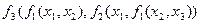 является формулой глубины 3, содержащей одну подформулу глубины 2 и две подформулы глубины 1.
является формулой глубины 3, содержащей одну подформулу глубины 2 и две подформулы глубины 1.
В дальнейшем конкретные формулы будем записывать в более привычном виде, при котором условные знаки функций стоят между аргументами (такую запись называют инфиксной). Например, если  является конъюнкцией,
является конъюнкцией, 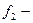 дизъюнкцией, а
дизъюнкцией, а  импликацией, то приведённая выше формула примет вид
импликацией, то приведённая выше формула примет вид 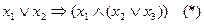 .
.
Все формулы, построенные подобным образом, то есть содержащие только символы переменных, скобки и знаки функций из множества  , называются формулами над множеством
, называются формулами над множеством  .
.
Возможны и другие интерпретации понятия глубины. Например, считается, что расстановка отрицаний над переменными не увеличивает глубины формулы. В случае, когда множество  содержит некоторую ассоциативную операцию
содержит некоторую ассоциативную операцию  , можно считать, что применение этой операции к формулам с той же внешней операцией
, можно считать, что применение этой операции к формулам с той же внешней операцией  не увеличивает глубины формулы. Например, формулы
не увеличивает глубины формулы. Например, формулы  и
и 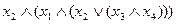 имеют одну и ту же глубину 3.
имеют одну и ту же глубину 3.
Всякая формула, выражающая данную функцию, как суперпозицию других функций, задаёт способ её вычисления (при условии, что известно, как вычислять исходные функции). Этот способ определяется следующим очевидным правилом: формулу можно вычислить, только если уже вычислены значения всех её подформул. Применим, например формулу 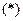 к набору
к набору  . Получим:
. Получим: 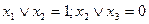 . Далее получим
. Далее получим 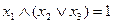 . Наконец,
. Наконец,  .
.
Таким образом, формула ставит в соответствие каждому набору значений аргументов значение функции и, значит, может наряду с таблицей служить способом задания и вычисления функции. В частности, по формуле, вычисляя её на всех 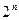 наборах, можно восстановить таблицу функции. О формуле, задающей функцию, говорят также, что она представляет или реализует функцию.
наборах, можно восстановить таблицу функции. О формуле, задающей функцию, говорят также, что она представляет или реализует функцию.
В отличие от табличного задания представление данной функции формулой не единственно. Например, если в качестве исходного множества функций зафиксировать функции 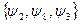 из предыдущего пункта (то есть функции И, ИЛИ, НЕ), то функцию
из предыдущего пункта (то есть функции И, ИЛИ, НЕ), то функцию 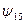 - штрих Шеффера – можно представить формулами
- штрих Шеффера – можно представить формулами 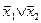 и
и 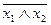 . Функцию
. Функцию  - стрелка Пирса – можно представить формулами
- стрелка Пирса – можно представить формулами  и
и  .
.
Определение. Формулы, представляющие одну и ту же функцию называются эквивалентными или равносильными.
Эквивалентность формул принято обозначать знаком равенства, поэтому можно записать:  .
.
Существует стандартный метод для выяснения эквивалентности двух формул. По каждой формуле восстанавливается таблица функции, а затем две полученные таблицы сравниваются. Таким способом в предыдущеё лекции мы устанавливали равносильность высказываний. Он весьма громоздок, так как требует 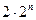 вычислений, если считать, что обе формулы зависят от
вычислений, если считать, что обе формулы зависят от 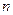 переменных. Более простыми методами, позволяющими устанавливать эквивалентность данных формул, а также получать новые формулы, эквивалентные исходной, являются эквивалентные преобразования, которые будут рассмотрены в дальнейшем.
переменных. Более простыми методами, позволяющими устанавливать эквивалентность данных формул, а также получать новые формулы, эквивалентные исходной, являются эквивалентные преобразования, которые будут рассмотрены в дальнейшем.
Назад, в начало конспекта.
Лекция № 9. Булевы алгебры.
В данной лекции будут рассмотрены способы представления логических функций в виде суперпозиций функций И, ИЛИ, НЕ.
- Разложение функций по переменным. Совершенная дизъюнктивная нормальная форма.
Введём обозначения: 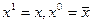 . Пусть
. Пусть 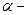 параметр, равный 0 или 1. Тогда
параметр, равный 0 или 1. Тогда 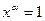 , если
, если  , и
, и 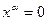 , если
, если 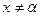 .
.
Теорема 8.1. Всякая логическая функция  может быть представлена в следующем виде:
может быть представлена в следующем виде:
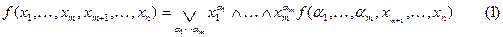 ,
,
где  , а дизъюнкция берётся по всем
, а дизъюнкция берётся по всем  наборам значений переменных
наборам значений переменных 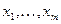 .
.
Равенство (1) называется разложением по переменным 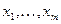 . Формула (1) достаточно громоздка на вид, однако её несложно использовать при небольших значениях
. Формула (1) достаточно громоздка на вид, однако её несложно использовать при небольших значениях 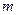 и
и 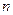 . Например, при значениях
. Например, при значениях 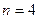 ,
, 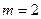 разложение (1) имеет вид:
разложение (1) имеет вид:
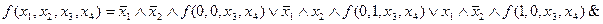
 .
.
Практический смысл такого разложения очевиден: оно позволяет заменять функцию нескольких переменных суперпозицией конечного числа функций с меньшим количеством переменных. Особенно важен частный случай 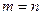 , когда разложение производится по всем переменным. При этом все переменные в правой части равенства (1) получают фиксированные значения, и функции в конъюнкциях правой части становятся равными 0 или 1, что даёт:
, когда разложение производится по всем переменным. При этом все переменные в правой части равенства (1) получают фиксированные значения, и функции в конъюнкциях правой части становятся равными 0 или 1, что даёт:
 ,
,
где дизъюнкция берётся по всем наборам  , на которых
, на которых 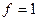 . Такое разложение называется совершенной дизъюнктивной нормальной формой (СДНФ) функции
. Такое разложение называется совершенной дизъюнктивной нормальной формой (СДНФ) функции  . СДНФ содержит ровно только конъюнкций, сколько единиц в таблице функции
. СДНФ содержит ровно только конъюнкций, сколько единиц в таблице функции  ; каждому единичному набору
; каждому единичному набору  соответствует дизъюнкция всех переменных, в которых
соответствует дизъюнкция всех переменных, в которых 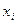 взято с отрицанием, если
взято с отрицанием, если 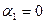 и без отрицания, если
и без отрицания, если  . Таким образом, существует взаимно однозначное соответствие между таблицей функции
. Таким образом, существует взаимно однозначное соответствие между таблицей функции  и её СДНФ. Следовательно, для каждой логической функции СДНФ является единственной (с точностью до порядка переменных и конъюнкций).
и её СДНФ. Следовательно, для каждой логической функции СДНФ является единственной (с точностью до порядка переменных и конъюнкций).
Пример 1. Составить СДНФ для функции, заданной таблицей:
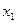
| 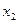
| 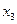
| 
|
Поскольку данная таблица (уже встречавшаяся ранее) содержит три единичных набора, СДНФ будет конъюнкцией трёх дизъюнкций. В свою очередь, каждая дизъюнкция включает три переменных – по числу их в функции  .
.
Получим:  .
.
Напомним, что, подобно знаку умножения, знак дизъюнкции 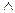 в логических формулах часто опускают. Тогда полученное выражение примет более компактный вид:
в логических формулах часто опускают. Тогда полученное выражение примет более компактный вид:
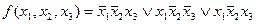 .
.
Единственная функция, которая не имеет СДНФ – это константа 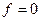 .
.
Формулы, содержащие кроме переменных и скобок, только знаки дизъюнкции, конъюнкции и отрицания, будем называть булевыми формулами.
Теорема 8.2. Всякая логическая функция может быть представлена булевой функцией, то есть как суперпозиция дизъюнкции, конъюнкции и отрицания.
- Булева алгебра функций.
Выше мы обозначили множество всех логических операций на двухэлементном множестве 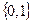 , как
, как  .
.
Определение. Булевой алгеброй логических функций называется алгебра вида  , основным множеством которой является всё множество логических функций, а операциями – дизъюнкция, конъюнкция и отрицание.
, основным множеством которой является всё множество логических функций, а операциями – дизъюнкция, конъюнкция и отрицание.
Замечание. На практике мы имеем дело не самими функциями, а с представляющими их формулами, то есть с алгеброй формул, которая значительно шире, поскольку каждую функцию представляет бесконечное множество формул. Чтобы “синхронизировать” их алгебре формул придаётся следующий вид. Элементами алгебры формул объявляются не сами формулы, а классы эквивалентности формул, то есть классы формул, представляющих одну и ту же функцию. Определённая таким образом, алгебра формул называется алгеброй Линденбаума - Тарского. Она изоморфна булевой алгебре функций.
Теперь рассмотрим основные свойства булевых операций (частично уже знакомые по теме “Элементы математической логики”).
1. Ассоциативность: а) 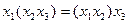 ; б)
; б) 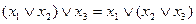 .
.
2. Коммутативность: а)  ; б)
; б)  .
.
3. Дистрибутивность конъюнкции относительно дизъюнкции:  .
.
4. Дистрибутивность дизъюнкции относительно конъюнкции:
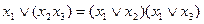 .
.
5. Идемпотентность: а) 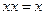 ; б)
; б) 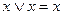 .
.
6. Двойное отрицание:  .
.
7. Свойства констант: а) 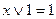 ; б)
; б)  ; в)
; в) 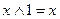 ; г)
; г) 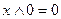 ; д)
; д) 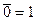 ; е)
; е) 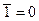 .
.
8. Правила де Моргана: а)  ; б)
; б)  . Очень важные соотношения, которые часто будут использоваться в дальнейшем. С их помощью (а также с помощью соотношения 6) дизъюнкция заменяется конъюнкцией и наоборот.
. Очень важные соотношения, которые часто будут использоваться в дальнейшем. С их помощью (а также с помощью соотношения 6) дизъюнкция заменяется конъюнкцией и наоборот.
9. Закон противоречия:  .
.
10. Закон “исключённого третьего”:  .
.
Все соотношения 1 – 10 можно проверить указанным ранее стандартным методом – вычислением обеих частей равенств на всех наборах значений переменных. Эти равенства остаются справедливыми и в случае подстановки вместо переменной любой логической функции и, следовательно, любой формулы, представляющей эту функцию. Важно лишь соблюдать следующее правило подстановки формулы вместо переменной.
При подстановке формулы 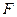 вместо переменной
вместо переменной  все вхождения данной переменной в исходное соотношение должны быть одновременно заменены формулой
все вхождения данной переменной в исходное соотношение должны быть одновременно заменены формулой 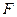 .
.
Правило подстановки позволяет получать из соотношений 1 – 10 новые эквивалентные соотношения. Заметим, что равенство  означает в данном контексте, что формулы
означает в данном контексте, что формулы  и
и  описывают одну и ту же логическую функцию. Следовательно, если какая-то формула
описывают одну и ту же логическую функцию. Следовательно, если какая-то формула 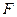 содержит
содержит  в качестве подформулы, то замена её на
в качестве подформулы, то замена её на  не изменит значения формулы
не изменит значения формулы 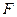 . Это утверждение представляет собой правило замены подформул, которое позволяет, используя эквивалентные соотношения, получать формулы, эквивалентные данной. Практическое применение описанных правил будет рассмотрено ниже.
. Это утверждение представляет собой правило замены подформул, которое позволяет, используя эквивалентные соотношения, получать формулы, эквивалентные данной. Практическое применение описанных правил будет рассмотрено ниже.
Замечание. Есть существенная разница между подстановкой и заменой. При подстановке переменная заменяется формулой; при этом формула может быть любой, лишь бы производилась одновременная замена ею всех вхождений переменной. При замене подформул может быть заменена любая подформула, однако, не на любую другую, а только на подформулу, эквивалентную ей. При этом замена всех вхождений исходной подформулы не обязательна.
- Эквивалентные преобразования.
Пример 2. Возьмём соотношение 8а и подставим вместо переменной 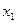 выражение
выражение  . Получим:
. Получим: 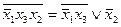 . Здесь в обеих частях стоят формулы, неэквивалентные исходным формулам, но эквивалентные между собой. Если же в правой части нового соотношения формулу
. Здесь в обеих частях стоят формулы, неэквивалентные исходным формулам, но эквивалентные между собой. Если же в правой части нового соотношения формулу  заменить формулой
заменить формулой  , эквивалентной ей в силу соотношения 8а и затем заменить
, эквивалентной ей в силу соотношения 8а и затем заменить  на
на 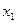 (согласно 6), то получим
(согласно 6), то получим 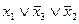 . Причём все формулы в полученной цепи преобразований являются эквивалентными:
. Причём все формулы в полученной цепи преобразований являются эквивалентными:
 .
.
Такие преобразования, использующие эквивалентные соотношения и правило замены, называют эквивалентными преобразованиями. Эквивалентные преобразования являются мощным средством доказательства эквивалентности формул, как правило, более эффективным, чем их вычисление на наборах значений переменных.
В булевой алгебре принято опускать скобки в следующих двух случаях: а) при последовательном выполнении нескольких конъюнкций или дизъюнкций; б) если они являются внешними скобками у конъюнкции. Оба соглашения совершенно аналогичны общепринятому опусканию скобок для операции умножения в арифметических выражениях.
Рассмотрим несколько способов упрощения формул с помощью эквивалентных преобразований, позволяющих получить формулы, содержащие меньшее количество символов.
а) Поглощение: 1)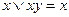 и 2)
и 2)  . Докажем данное равенство подробно, используя для доказательства соотношения 3, 7а и 7в.
. Докажем данное равенство подробно, используя для доказательства соотношения 3, 7а и 7в.
 .
.
Далее будем опускать доказательства приводимых равенств, которые при желании можно получить из соотношений 1 – 10 и уже доказанных равенств.
б) Склеивание: 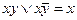 .
.
в) Обобщённое склеивание:  .
.
г) 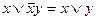 .
.
Одним из главных видов упрощения формул является приведение их к дизъюнктивной нормальной форме (ДНФ).
Определение. Элементарными конъюнкциями называются конъюнкции переменных или их отрицаний, в которых каждая переменная встречается не более одного раза. Дизъюнктивной нормальной формой называется формула, имеющая вид дизъюнкции элементарных конъюнкций.
Заметим, что СДНФ является частным случаем ДНФ.
Приведение формулы к ДНФ выполняется так. Сначала с помощью соотношений 6 и 8 все отрицания “спускаются” до переменных. Затем раскрываются скобки. После этого с помощью соотношений 5, 9 и 10 удаляются лишние конъюнкции и повторения переменных в конъюнкциях. Наконец, с помощью соотношений 7а – 7е удаляются лишние константы. При этом необходимо помнить, что ДНФ данной формулы может быть не единственной.
Пример 3. Привести к ДНФ формулу 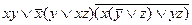 .
.
Решение:



 . В итоге получили дизъюнкцию элементарных конъюнкций, то есть ДНФ.
. В итоге получили дизъюнкцию элементарных конъюнкций, то есть ДНФ.
Доказано, что если из формулы  можно с помощью эквивалентных преобразований получить формулу
можно с помощью эквивалентных преобразований получить формулу  , то можно из формулы
, то можно из формулы  (с помощью тех же соотношений) получить формулу
(с помощью тех же соотношений) получить формулу  . Иначе говоря, всякое эквивалентное преобразование обратимо. Это позволяет сформулировать следующую теорему.
. Иначе говоря, всякое эквивалентное преобразование обратимо. Это позволяет сформулировать следующую теорему.
Теорема 8.3. Для любых двух эквивалентных формул  и
и  существует эквивалентное преобразование
существует эквивалентное преобразование  в
в  и наоборот с помощью соотношений 1 – 10.
и наоборот с помощью соотношений 1 – 10.
Аналогично понятию ДНФ определяется понятие конъюнктивной нормальной формы (КНФ), то есть КНФ есть конъюнкция элементарных дизъюнкций. Переход от КНФ к ДНФ и обратно всегда осуществим (обычно, с помощью формул Де Моргана).
Пример 4. Привести формулу  к КНФ.
к КНФ.
Заменим исходную формулу её двойным отрицанием, а затем применим соотношения 8.



 .
.
Назад, в начало конспекта.
Лекция № 10. Булевы алгебры и теория множеств.
- Двойственность.
Определение. Функция  называется двойственной к функции
называется двойственной к функции 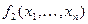 , если
, если  .
.
Если взять отрицание обеих частей равенства и подставить 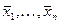 вместо переменных
вместо переменных  , то получится
, то получится 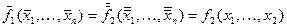 . Это означает, что функция
. Это означает, что функция  двойственна к функции
двойственна к функции  , и, таким образом, отношение двойственности является симметричным. Из определения двойственности ясно, что для любой функции двойственная ей функция определяется однозначно. В частности, может оказаться, что функция двойственна самой себе. В этом случае она называется самодвойственной.
, и, таким образом, отношение двойственности является симметричным. Из определения двойственности ясно, что для любой функции двойственная ей функция определяется однозначно. В частности, может оказаться, что функция двойственна самой себе. В этом случае она называется самодвойственной.
Пример 1. Если рассматривать логические функции, то, очевидно, дизъюнкция двойственна конъюнкции и наоборот (непосредственно следует из правил Де Моргана). Отрицание является самодвойственной функцией. Функция-константа 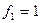 двойственна функции
двойственна функции 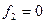 . Ещё один традиционный пример самодвойственной функции – функция
. Ещё один традиционный пример самодвойственной функции – функция  .
.
Пользуясь определением двойственности нетрудно доказать следующее утверждение, называемое принципом двойственности.
Теорема 10.1. Если в формуле 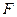 , представляющей функцию
, представляющей функцию  , все знаки функций заменить соответственно на знаки двойственных им функций, то полученная формула
, все знаки функций заменить соответственно на знаки двойственных им функций, то полученная формула 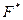 будет представлять функцию
будет представлять функцию  , двойственную функции
, двойственную функции  .
.
В булевой алгебре принцип двойственности имеет более конкретный вид, вытекающий из ранее приведённых примеров: если в формуле 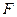 , представляющей функцию
, представляющей функцию  , все конъюнкции заменить дизъюнкциями и наоборот, все единицы заменить нулями и наоборот, то получим формулу
, все конъюнкции заменить дизъюнкциями и наоборот, все единицы заменить нулями и наоборот, то получим формулу 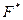 , представляющую функцию
, представляющую функцию  , двойственную функции
, двойственную функции  .
.
Если функции равны, то двойственные им функции также равны. Это позволяет с помощью принципа двойственности получать новые эквивалентные соотношения, переходя от равенства  с помощью указанных замен к равенству
с помощью указанных замен к равенству  . Примером могут служить соотношения
. Примером могут служить соотношения  и
и  , которые могут быть получены друг из друга по указанному принципу.
, которые могут быть получены друг из друга по указанному принципу.
- Булева алгебра и теория множеств.
Ранее были описаны булевы алгебры множеств, то есть алгебры вида  , где
, где 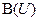 - булеан множества
- булеан множества 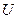 , то есть множество всех его подмножеств. Общий термин “булева алгебра” для алгебр множеств и логических функций не является случайным.
, то есть множество всех его подмножеств. Общий термин “булева алгебра” для алгебр множеств и логических функций не является случайным.
Определение. Всякая алгебра типа  называется булевой алгеброй, если её операции удовлетворяют соотношениям 1 – 10 (см. предыдущую лекцию).
называется булевой алгеброй, если её операции удовлетворяют соотношениям 1 – 10 (см. предыдущую лекцию).
В алгебре множеств элементами являются подмножества фиксированного универсального множества 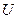 . В этой алгебре операция пересечения соответствует конъюнкции, операция объединения соответствует дизъюнкции, а операция дополнения соответствует отрицанию. Само множество
. В этой алгебре операция пересечения соответствует конъюнкции, операция объединения соответствует дизъюнкции, а операция дополнения соответствует отрицанию. Само множество 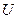 является единицей, а пустое множество – нулём. Справедливость соотношений 1 – 10 для этой алгебры можно доказать непосредственно, рассматривая в них переменные как множества, а знаки логических функций – как соответствующие операции над множествами.
является единицей, а пустое множество – нулём. Справедливость соотношений 1 – 10 для этой алгебры можно доказать непосредственно, рассматривая в них переменные как множества, а знаки логических функций – как соответствующие операции над множествами.
В одной из предыдущих лекций отмечалось взаимно однозначное соответствие между множеством 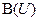 , где
, где  и множеством
и множеством  двоичных векторов длины
двоичных векторов длины 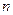 . Каждому подмножеству
. Каждому подмножеству 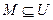 соответствует двоичный вектор
соответствует двоичный вектор  , где
, где  , если
, если 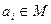 , и
, и  , если
, если  . Операции над векторами в булевой алгебре
. Операции над векторами в булевой алгебре 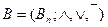 определяются следующим образом.
определяются следующим образом.
Пусть даны два вектора 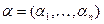 и
и 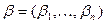 из множества
из множества  . Тогда:
. Тогда:
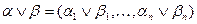 ,
,
 ,
,
 .
.
Поскольку компоненты (координаты) векторов принимают значения 0 или 1, то указанные операции – это просто логические операции над двоичными переменными, поэтому операции над векторами естественно назвать покомпонентными логическими операциями над двоичными векторами.
Пример 2. Даны векторы  и
и 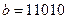 . Найти
. Найти  .
.
Решение:
 .
.
Заметим, что подобные операции (наряду с логическими операциями над переменными) входят в систему команд любой современной ЭВМ.
Теорема 10.2. Если мощность множества 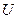 равна
равна 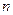
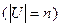 , то булева алгебра
, то булева алгебра 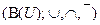 изоморфна булевой алгебре
изоморфна булевой алгебре  .
.
Эта простая по содержанию теорема имеет огромное значение в математике. Она позволяет заменить теоретико-множественные операции над системой подмножеств данного множества поразрядными логическими операциями над двоичными векторами.
Похожая по формулировке, но значительно отличающаяся по смыслу теорема существует для множества всех логических функций 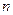 переменных
переменных  . Обозначим это множество
. Обозначим это множество 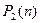 . Оно замкнуто относительно операций
. Оно замкнуто относительно операций  и, следовательно, образует конечную булеву алгебру
и, следовательно, образует конечную булеву алгебру  , которая является подалгеброй булевой алгебры логических функций.
, которая является подалгеброй булевой алгебры логических функций.
Теорема 10.3. Если мощность множества 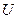 равна
равна 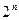
 , то булева алгебра
, то булева алгебра 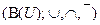 изоморфна булевой алгебре функций
изоморфна булевой алгебре функций  .
.
Теорема 10.3 указывает на тесную связь между множествами и логическими функциями и позволяет переходить от операций над множествами к операциям над функциями и обратно. В частности, они позволяют непосредственно производить операции над функциями, заданными не формулами, а таблицами. Пример приведён в следующей таблице, содержащей две функции трёх переменных  и
и 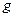 и результаты операций над ними:
и результаты операций над ними:
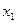
| 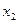
| 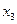
| 
| 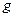
| 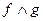
| 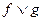
| 
|
- ДНФ, интервалы и покрытия.
Теоретико-множественная интерпретация булевой алгебры предлагает очень удобный язык для изучения дизъюнктивных нормальных форм (ДНФ) и построения методов их упрощения. Рассмотрим кратко основные понятия, связанные с ДНФ.
Введём следующее обозначение: обозначим через 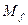 множество всех единичных наборов функции
множество всех единичных наборов функции  . Тогда набор (вектор)
. Тогда набор (вектор)  из множества
из множества  принадлежит
принадлежит 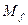 тогда и только тогда, когда
тогда и только тогда, когда 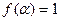 . Множество
. Множество 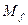 называется единичным множеством функции
называется единичным множеством функции  , а функция
, а функция  называется характеристической функцией множества
называется характеристической функцией множества 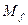 . Легко показать, что соответствие между функциями и их единичными множествами является изоморфизмом.
. Легко показать, что соответствие между функциями и их единичными множествами является изоморфизмом.
Если функция  представляется элементарной конъюнкцией всех
представляется элементарной конъюнкцией всех 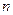 переменных, то множество
переменных, то множество 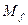 содержит ровно один элемент множества
содержит ровно один элемент множества  . Если же функция – элементарная конъюнкция
. Если же функция – элементарная конъюнкция  переменных
переменных 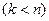 , то
, то 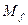 содержит
содержит 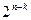 двоичных наборов. Это объясняется тем, что в таком случае
двоичных наборов. Это объясняется тем, что в таком случае 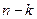 переменных, не входящих в эту конъюнкцию несущественны для функции
переменных, не входящих в эту конъюнкцию несущественны для функции  . Тогда они принимают
. Тогда они принимают 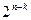 значений, не изменяя значения
значений, не изменяя значения  . Множество
. Множество 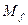 такой функции называется интервалом.
такой функции называется интервалом.
Пример 3. Рассмотрим функцию 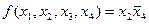 и найдём её интервал.
и найдём её интервал.
Прежде всего, заметим, что две переменных 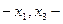 являются несущественными. Это позволяет сразу определить количество единичных наборов, содержащихся в множестве
являются несущественными. Это позволяет сразу определить количество единичных наборов, содержащихся в множестве  (иначе говоря, его мощность). Поскольку в данном случае
(иначе говоря, его мощность). Поскольку в данном случае  , то получим
, то получим  .
.
Далее, очевидно, что 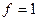 только при значениях
только при значениях 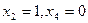 . При этом переменные
. При этом переменные 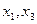 могут принимать любые значения. Теперь перечислим все единичные наборы для данной функции:
могут принимать любые значения. Теперь перечислим все единичные наборы для данной функции:  . Итак,
. Итак,  .
.
В рассматриваемом случае говорят, что конъюнкция  (или, точнее, интервал
(или, точнее, интервал  ) покрывает множество
) покрывает множество 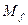 и все его подмножества.
и все его подмножества.
Представление некоторой функции в виде ДНФ соответствует представлению её единичного множества в виде объединения интервалов; в совокупности все конъюнкции ДНФ покрывают всё единичное множество функции  . Обратное также верно: если все элементы некоторого интервала
. Обратное также верно: если все элементы некоторого интервала  принадлежат
принадлежат 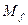 , то существует ДНФ данной функции, содержащая конъюнкцию
, то существует ДНФ данной функции, содержащая конъюнкцию  .
.
Назад, в начало конспекта.
Лекция № 11. Полнота и замкнутость.
Ранее нами рассматривались два способа задания логических функций – табличный и с помощью формул. Таблица задаёт функцию непосредственно как соответствие между двоичными наборами и значениями функции на этих наборах. Этот способ универсален, то есть, пригоден для любых функций, однако слишком громоздок. Формула – гораздо более компактный способ задания функции, но она задаёт функцию через другие функции. Поэтому для любой системы функций  возникает естественный вопрос: всякая ли логическая функция представима формулой в этой системе. В позапрошлой лекции был получен положительный ответ для системы
возникает естественный вопрос: всякая ли логическая функция представима формулой в этой системе. В позапрошлой лекции был получен положительный ответ для системы 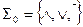 (теорема 8.2). В данной лекции будет показано, как решать этот вопрос для произвольной системы
(теорема 8.2). В данной лекции будет показано, как решать этот вопрос для произвольной системы  .
.
- Функционально полные системы.
Определение. Система функций  называется функционально полной системой, если любая логическая функция может быть представлена формулой над системой
называется функционально полной системой, если любая логическая функция может быть представлена формулой над системой  (является суперпозицией функций этой системы).
(является суперпозицией функций этой системы).
Из теоремы 8.2 следует, что система 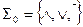 является функционально полной. Равным образом, функционально полна любая система
является функционально полной. Равным образом, функционально полна любая система  , через функции которой можно выразить конъюнкцию, дизъюнкцию и отрицание. Действительно, для любой логической функции
, через функции которой можно выразить конъюнкцию, дизъюнкцию и отрицание. Действительно, для любой логической функции  из такой системы следует составить булеву формулу (а она обязательно существует согласно теореме 8.2) и потом выразить в ней конъюнкцию, дизъюнкцию и отрицание через функции системы
из такой системы следует составить булеву формулу (а она обязательно существует согласно теореме 8.2) и потом выразить в ней конъюнкцию, дизъюнкцию и отрицание через функции системы  . Аналогично обосновывается более общее утверждение.
. Аналогично обосновывается более общее утверждение.
Теорема 11.1. Если все функции функционально полной системы 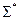 представимы формулами над системой
представимы формулами над системой  , то система
, то система  также функционально полна.
также функционально полна.
Пример 1.
а) Системы  и
и 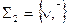 функционально полны. Действительно, с помощью законов Де Моргана и двойного отрицания можно выразить в каждой из этих систем функцию, недостающую до
функционально полны. Действительно, с помощью законов Де Моргана и двойного отрицания можно выразить в каждой из этих систем функцию, недостающую до 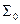 через остальные две:
через остальные две:
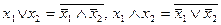 .
.
С точки зрения функциональной полноты систему 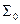 следует считать избыточной: она сохраняет свойство полноты и при удалении из неё конъюнкции или дизъюнкции. Однако легко видеть из приведённого примера, что, хотя системы
следует считать избыточной: она сохраняет свойство полноты и при удалении из неё конъюнкции или дизъюнкции. Однако легко видеть из приведённого примера, что, хотя системы  и
и 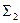 не являются избыточными, зато формулы в них получаются гораздо длиннее: замена одной операции на другую вносит в формулу сразу три лишних отрицания.
не являются избыточными, зато формулы в них получаются гораздо длиннее: замена одной операции на другую вносит в формулу сразу три лишних отрицания.
б) Системы 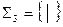 (штрих Шеффера) и
(штрих Шеффера) и 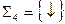 (стрелка Пирса) являются функционально полными.
(стрелка Пирса) являются функционально полными.
 .
.
Таким образом, система  сводится к системе
сводится к системе  , а система
, а система 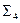 - к системе
- к системе 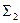 .
.
в) Система  (
(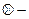 умножение по модулю 2,
умножение по модулю 2,  сложение по модулю 2 – см. пункт 1 лекции № 8)) является функционально полной. Поскольку
сложение по модулю 2 – см. пункт 1 лекции № 8)) является функционально полной. Поскольку 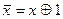 , данная система сводится к
, данная система сводится к 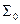 .
.
На свойствах этой системы остановимся подробнее.
- Алгебра Жегалкина и линейные функции.
Определение. Алгебра над множеством логических функций с двумя бинарными операциями  называется алгеброй Жегалкина.
называется алгеброй Жегалкина.
Замечание. Операция 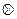 вполне аналогична операции конъюнкции (логического умножения). Однако операция
вполне аналогична операции конъюнкции (логического умножения). Однако операция  имеет совершенно другой математический смысл, чем дизъюнкция (соответствующая функция ранее была названа неравнозначностью). Поэтому никак нельзя считать алгебру Жегалкина иной формой записи булевой алгебры.
имеет совершенно другой математический смысл, чем дизъюнкция (соответствующая функция ранее была названа неравнозначностью). Поэтому никак нельзя считать алгебру Жегалкина иной формой записи булевой алгебры.
В алгебре Жегалкина выполняются следующие соотношения (знак умножения 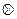 опущен):
опущен):
2.1.  ,
,
2.2. 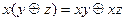 ,
,
2.3 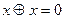 ,
,
2.4 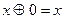 .
.
Кроме того, выполняются соотношения, ранее сформулированные булевой алгебры, относящиеся к конъюнкции и константам. Отрицание и дизъюнкция выражаются так:
2.5 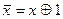 ,
,
2.6 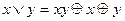 .
.
Если в произвольной формуле алгебры Жегалкина раскрыть скобки и произвести все упрощения по вышеуказанным соотношениям, то получится формула, имеющая вид Суммы произведений, то есть полином (многочлен) по модулю 2. Такая формула называется полиномом Жегалкина для данной функции.
От булевой формулы всегда можно перейти к формуле алгебры Жегалкина, используя равенства 2.5 и 2.6, а также прямое следствие из равенства 2.6: если  , то
, то 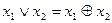 . Оно, в частности, позволяет заменять знак дизъюнкции знаком
. Оно, в частности, позволяет заменять знак дизъюнкции знаком  в случаях, когда исходная формула представляет собой СДНФ.
в случаях, когда исходная формула представляет собой СДНФ.
Пример 2. Составить полиномы Жегалкина для данных функций:
а) 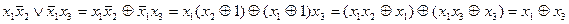 ,
,
б)  .
.
Заметим, что если в полученных полиномах Жегалкина произвести обратную замену функций, то получим упрощённые формулы булевой алгебры.
Теорема 11.2. Для всякой логической функции существует полином Жегалкина и притом единственный.
Существование такого полинома, по сути, уже доказано, а для доказательства его единственности достаточно показать существование взаимно однозначного соответствия между множеством всех функций 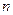 переменных и множеством всех полиномов Жегалкина.
переменных и множеством всех полиномов Жегалкина.
Определение. Функция, у которой полином Жегалкина имеет вид  , где параметры
, где параметры  равны нулю или единице, называется линейной.
равны нулю или единице, называется линейной.
Все функции от одной переменной линейны. Также линейными являются функции эквивалентность и сумма по модулю 2.
- Замкнутые классы. Монотонные функции.
Определение. Множество  логических функций называется замкнутым классом, если любая суперпозиция функций из множества
логических функций называется замкнутым классом, если любая суперпозиция функций из множества  снова принадлежит
снова принадлежит  .
.
Всякая система  логических функций порождает некоторый замкнутый класс, а именно класс всех функций, которые можно получить суперпозициями функций
логических функций порождает некоторый замкнутый класс, а именно класс всех функций, которые можно получить суперпозициями функций  . Такой класс называется замыканием
. Такой класс называется замыканием  и обозначается
и обозначается  . Если множество
. Если множество  - функционально полная система, то
- функционально полная система, то 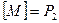 .
.
Пример 3.
а) Множество всех дизъюнкций, то есть функций вида 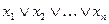 является замкнутым классом.
является замкнутым классом.
б) Множество всех линейных функций является замкнутым классом, так как подстановка формул вида  после преобразований даёт формулу такого же вида.
после преобразований даёт формулу такого же вида.
Важнейшим примером замкнутого класса является класс монотонных функций, который будет рассмотрен далее.
Ранее рассматривалось отношение частичного порядка  на множестве векторов одинаковой длины. Напомним, что для векторов
на множестве векторов одинаковой длины. Напомним, что для векторов 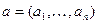 и
и 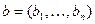 выполняется
выполняется  , если для любого
, если для любого  выполняется
выполняется 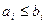 . Здесь воспользуемся этим отношением для двоичных векторов.
. Здесь воспользуемся этим отношением для двоичных векторов.
Определение. Функция  называется монотонной, если для любых двух двоичных наборов длины
называется монотонной, если для любых двух двоичных наборов длины 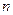 из того, что
из того, что  следует
следует  .
.
Пример 4.
а) Функция  монотонна.
монотонна.
б) Дизъюнкция и конъюнкция любого числа переменных являются монотонными функциями.
в) Рассмотрим две функции от трёх переменных, заданных следующей таблицей.
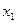
| 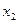
| 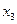
| 
| 
|
Функция  , очевидно, не является монотонной, так как, например
, очевидно, не является монотонной, так как, например 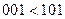 , а
, а  . Монотонность функции
. Монотонность функции  легко установить непосредственной проверкой.
легко установить непосредственной проверкой.
Проверка монотонности функции непосредственно по определению требует анализа таблицы функции и может оказаться достаточно трудоёмкой. Поэтому весьма полезной для установления монотонности является следующая теорема. Всякая булева формула, не содержащая отрицаний, представляет собой монотонную функцию отличную от константы; наоборот, для любой монотонной функции, отличной от 0 и 1, найдётся представляющая её булева формула без отрицаний.
Теорема 11.3. Всякая булева формула, не содержащая отрицаний, представляет собой монотонную функцию отличную от константы; наоборот, для любой монотонной функции, отличной от 0 и 1, найдётся представляющая её булева формула без отрицаний.
Из данной теоремы и того очевидного факта, что подстановка нескольких формул без отрицаний в формулу без отрицаний снова даёт формулу без отрицаний, вытекает следующая теорема.
Теорема 11.4. Множество всех монотонных функций является замкнутым классом.
Но поскольку всякая булева формула без отрицаний является суперпозицией дизъюнкций и конъюнкций, из данной теоремы непосредственно получаем следствие.
Следствие. Класс монотонных функций является замыканием системы функций  .
.
- Теоремы о функциональной полноте.
Теперь перейдём к рассмотрению основного вопроса, поставленного в рамках данной лекции: каковы необходимые и достаточные условия функциональной полноты для произвольной системы функций  ? Вначале было сказано, что система
? Вначале было сказано, что система  полна, если конъюнкция, дизъюнкция и отрицание являются суперпозициями функций из системы
полна, если конъюнкция, дизъюнкция и отрицание являются суперпозициями функций из системы  . Поэтому будем искать свойства функций, позволяющие выразить через них булевы операции. Сначала сформулируем две леммы, позволяющие вывести соответствующие теоремы.
. Поэтому будем искать свойства функций, позволяющие выразить через них булевы операции. Сначала сформулируем две леммы, позволяющие вывести соответствующие теоремы.
Лемма 1 (о немонотонных функциях). Если функция  немонотонна, то подстановкой констант из неё можно получить отрицание.
немонотонна, то подстановкой констант из неё можно получить отрицание.
Практически данная лемма является утверждением, противоположным теореме, обратной к теореме 11.3. Смысл её заключается в том, что для функции  существует такая подстановка
существует такая подстановка  константы, что функция оставшейся одной переменной является отрицанием.
константы, что функция оставшейся одной переменной является отрицанием.
Лемма 2 (о нелинейных функциях). Если функция  нелинейна, то с помощью подстановки констант и использования отрицаний из неё можно получить дизъюнкцию или конъюнкцию.
нелинейна, то с помощью подстановки констант и использования отрицаний из неё можно получить дизъюнкцию или конъюнкцию.
Иначе говоря, существует представление дизъюнкции и конъюнкции в виде суперпозиции констант, отрицаний и нелинейной функции  .
.
Замечание. При традиционных обозначениях переменных в выражениях вида  , где переменные расположены в естественном порядке индексов, эти индексы играют двоякую роль: они именуют переменные и нумеруют их места в функции. Эти роли следует различать.
, где переменные расположены в естественном порядке индексов, эти индексы играют двоякую роль: они именуют переменные и нумеруют их места в функции. Эти роли следует различать.
Две указанные леммы позволяют получить все булевы операции с помощью немонотонных функций, нелинейных функций и констант. Это ещё не полнота в точном смысле слова, так как константы с самого начала предполагались данными. Однако такое предположение часто бывает оправданным в различных приложениях (прежде всего в синтезе логических схем). Поэтому есть смысл ввести ослабленное определение полноты.
Определение. Система функций  называется функционально полной в слабом смысле, если любая логическая функция может быть представлена формулой над системой
называется функционально полной в слабом смысле, если любая логическая функция может быть представлена формулой над системой  , то есть является суперпозицией констант и функций из системы
, то есть является суперпозицией констант и функций из системы