М.13.16. В чем заключается постановка прямой и обратной задач теории предельного равновесия сыпучей среды?

М.13.14. Каким образом влияет удельное сцепление в зоне простейшего напряженного состояния на боковые напряжения s x при заданном напряжении s z?

М.13.13. Какие простейшие задачи теории предельного равновесия сыпучей среды решаются в замкнутом виде?

М.13.11. Как ставятся конкретные задачи в теории предельного равновесия сыпучей среды?

Конкретные задачи ставятся следующим образом: на одной части границы области заданы напряжения по величине и по направлению. Требуется отыскать величину (при заданном направлении действия) или направление (при заданной величине) напряжений на соседней части границы области, исходя из того, что в каждой точке области имеет место предельное состояние.

М.13.12*. Имеется ли единственность в постановке задач в теории предельного равновесия сыпучей среды и в теории упругости?

В теории предельного равновесия такой единственности нет, поскольку основным уравнением предельного равновесия является квадратное уравнение относительно напряжений. Поэтому имеет место двойственность, и правильную постановку задачи подсказывают результаты экспериментальных исследований. В теории упругости вся система линейная, поэтому имеет место единственность решения задач.

Простейшие задачи, решаемые в теории предельного равновесия в замкнутом виде, - это задачи об активном и пассивном давлениях грунта на подпорную стену при ее гладкой вертикальной поверхности, примыкающей к засыпке, и при горизонтальной поверхности грунта засыпки. Также решается задача о грунтовой трубе, находящейся в предельном состоянии под действием давления изнутри (или снаружи). Имеются еще некоторые задачи, но число их весьма ограничено.

В зоне минимального напряженного состояния (зоне активного давления) величина s _x с ростом сцепления c уменьшается, а в зоне максимального напряженного состояния (зоне пассивного давления) величина s _x с ростом сцепления c увеличивается.

М.13.15*. Откуда произошло название зон с простейшим напряженным состоянием - зоны минимально напряженного состояния и зоны максимально напряженного состояния?

Зона минимального напряженного состояния называется так потому, что эллипс напряжений в ней имеет наименьшую ось горизонтальной и быть "тоньше" не может (при той же вертикальной оси). Зона максимального напряженного состояния имеет "лежачий" эллипс напряжений и горизонтальная ось эллипса быть больше не может (при той же вертикальной оси). Таким образом, горизонтальная ось эллипса при неизменной вертикальной оси определяет эти названия.

В прямой задаче об основании задана нагрузка по величине и направлению и отыскивается величина пригрузки (при заданном ее направлении) или направление (при заданной ее величине). В обратной задаче об основании задана пригрузка (по величине и направлению) и отыскиваются величина нагрузки (при заданном ее направлении) или ее направление (при заданной величине). Таким образом, три условия всегда оказываются заданными, а одно подлежит определению.

М.13.17*. Для чего нужна переходная зона между зонами с максимальным и минимальным напряженными состояниями в задачах теории предельного равновесия сыпучей среды?

Включение в рассмотрение переходной зоны (зона III на рис.М.12.11) позволяет получить непрерывность всех компонентов напряжений при переходе из одной зоны в другую и плавный поворот осей эллипсов напряжений.

М.13.18*. Чем отличаются разрывное и неразрывное решения и какие компоненты напряжений претерпевают разрыв?

Разрывное и неразрывное решения задачи об основании дают резко различную величину несущей способности.

В этой задаче при переходе от зоны с минимальным напряженным состоянием к зоне с максимальным напряженным состоянием претерпевает разрыв на границе зон вертикальное напряжение s _z, а напряжение s _x является непрерывным (в обеих зонах t _xz = 0).

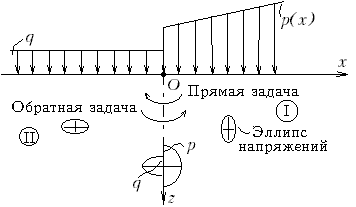
Рис.М.13.18. Схема для определения предельной нагрузки на основание в предположении существования разрыва в напряжении s _z слева и справа от оси x =0

М.13.19. Какой вид имеет формула несущей способности по Прандтлю и что получается, если среда не обладает трением (j =0)?

Формула несущей способности p, кПа, по Прандтлю (в ней рассматривается сыпучая среда) имеет следующий вид:

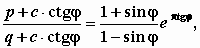
где q - пригрузка, кПа.

При разрывном решении эта формула выглядит так:

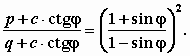
Если среда не обладает трением, то из первой формулы получим (по Прандтлю)

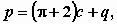
а из второй

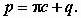
М.13.20*. Где располагается "особая точка" и каковы ее свойства?

"Особая точка" (cм.рис.М.13.18, точка О) располагается в месте, где кончается нагрузка и начинается пригрузка, то есть имеет место скачок в величине усилий, приложенных на границе. Особая точка обладает тем свойством, что при подходе к ней по различным лучам мы получаем различие напряжения от наибольшего (нагрузка) до наименьшего (пригрузка). Таким образом, в особой точке имеет место многозначность напряжений.

Дата добавления: 2014-01-04