Прямые многократные измерения

Точно оценить действительное значение измеряемой величины можно лишь путем её многократных измерений и соответствующей обработки их результатов. Правильно обработать полученные результаты наблюдений – значит получить наиболее точную оценку действительного значения измеряемой величины и доверительного интервала, в котором находится её истинное значение. Обработка должна производиться в соответствии с ГОСТ 8.207–76 «ГСИ. Прямые измерения с многократными наблюдениями. Методы обработки результатов наблюдений. Общие положения». В процессе обработки результатов наблюдений необходимо последовательно решить следующие основные задачи:

- определить точечные и интегральные оценки закона распределения результатов измерений;

- исключить «промахи» (по одному из критериев);

- устранить систематические погрешности измерений (см. 3.1);

- оценить закон распределения по статистическим критериям (используются критерии χ²-Пирсона, Колмогорова);

- определить доверительные границы неисключённого остатка систематической составляющей, случайной составляющей и общей погрешности результата измерения (см. 3.2.2);

- записать результат измерения (см. 3.2.2).

Основными точечными характеристиками погрешности измерений, которые оцениваются расчётным путём (до проведения измерений) по характеристикам используемых методов и средств измерений или по результатам измерений (после осуществления измерительного процесса), являются математическое ожидание и среднеквадратичное отклонение. Оценкой математического ожидания (МО) случайной величины является среднеарифметическое значение измеряемой величины

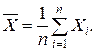(1)

Для получения характеристики рассеивания результатов вокруг среднего арифметического значения в абсолютных единицах используют среднеквадратичное отклонение

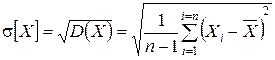. (2)

Точечные оценки, характеризующие параметры распределения в виде чисел, обычно используют при большом объёме выборки. С уменьшением объёма выборки степень их достоверности уменьшается, поэтому переходят к интервальным оценкам, позволяющим определить интервал (доверительный), в котором с заданной вероятностью (доверительной) находится истинное значение оцениваемого параметра.

Вероятность того, что действительное значение измеряемой величины X находится внутри доверительного интервала (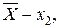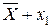), называется надёжностью 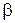при заданной точности.

В практике измерений применяют различные значения доверительной вероятности, например: 0,90; 0,95; 0,98; 0,99; 0,9973 и 0,999. Доверительный интервал и доверительную вероятность выбирают в зависимости от конкретных условий измерений. Так, например, при нормальном законе распределения случайных погрешностей со средеквадратичным отклонением 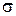часто пользуются доверительным интервалом от до 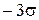, для которого доверительная вероятность (по статистическим таблицам значений функции Лапласа) равна 0,9973. Такая доверительная вероятность означает, что в среднем из 370 случайных погрешностей только одна погрешность по абсолютному значению будет больше 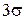. Так как на практике число отдельных измерений редко превышает несколько десятков, появление даже одной случайной погрешности, большей 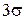, маловероятное событие, наличие же двух подобных погрешностей почти невозможно. Это позволяет с достаточным основанием утверждать, что все возможные случайные погрешности измерения, распределённые по нормальному закону, практически не превышают по абсолютному значению 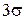(правило «трёх сигм»). В случае, если погрешность выходит за значение 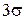, то его можно считать «промахом». Для определения «промаха» используют критерии «трёх сигм» – Смирнова, Райта, Романовского, Шовенэ и др.

Проверка гипотез о законе распределения

Одной из важнейших задач математической статистики является установление теоретического закона распределения случайной величины, характеризующей изучаемый признак по опытному (эмпирическому) распределению, представляющему вариационный ряд.

Для решения этой задачи необходимо определить вид и параметры закона распределения.

Предположение о виде закона распределения может быть выдвинуто исходя из теоретических предпосылок (например, выполнение условий центральной предельной теоремы может свидетельствовать о нормальном законе распределения случайной величины), опыта аналогичных предшествующих исследований и, наконец, на основании графического изображения эмпирического распределения.

Параметры распределения, как правило, неизвестны, поэтому их заменяют наилучшими оценками по выборке.

Как бы хорошо ни был подобран теоретический закон распределения, между эмпирическим и теоретическим распределениями неизбежны расхождения. Естественно, возникает вопрос: объясняются ли эти расхождения только случайными обстоятельствами, связанными с ограниченным числом наблюдений, или они являются существенными и связаны с тем, что теоретический закон распределения подобран неудачно. Для ответа на этот вопрос и служат критерии согласия.

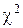-критерий Пирсона. В наиболее часто используемом на практике критерии 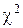-Пирсона в качестве меры расхождения берётся величина 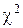, равная сумме квадратов отклонений частостей (статистических вероятностей) w_i от гипотетических p_i, рассчитанных по предполагаемому распределению, взятых с некоторыми весами с_i:

.

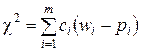Веса с_i вводятся таким образом, чтобы при одних и тех же отклонениях 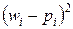больший вес имели отклонения, при которых p_i мала, и меньший вес – при которых p_i велика. Очевидно, этого удаётся достичь, если взять с_i обратно пропорциональными вероятностям p_i. Взяв в качестве весов 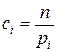, можно доказать, что при 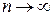стати-стика

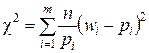
или

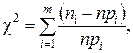
имеет 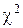-распределение с k = m - r -1 степенями свободы, где m – число интервалов эмпирического распределения (вариационного ряда); r – число параметров теоретического распределения, вычисленных по экспериментальным данным.

Числа n_i = n w_i и np_i называются, соответственно, эмпиричес-кими и теоретическими частотами.

Схема применения критерия 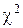сводится к следующему:

1. Определяется мера расхождения эмпирических и теоретических частот .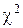

2. Для выбранного уровня значимости (по табл. 7, см. с. 36) 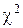-распределения находят критическое значение 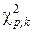при числе степеней свободы k = m - r -1.

3. Если фактически наблюдаемое значение 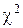больше критического, т.е. 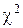> 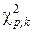, то гипотеза отвергается, если 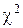≤ 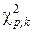, гипотеза не противоречит опытным данным.

Критерий Колмогорова. На практике кроме критерия 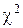часто используется критерий Колмогорова, в котором в качестве меры расхождения между теоретическим и эмпирическим распределениями рассматривают максимальное значение абсолютной величины разности между эмпирической функцией распределения F_n(x) и соответствующей теоретической функцией распределения

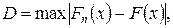
называемое статистикой критерия Колмогорова.

Доказано, что какова бы ни была функция распределения F(x) непрерывной случайной величины X, при неограниченном увеличении числа наблюдений (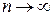) вероятность неравенства 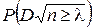стремится к пределу

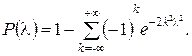
Задавая уровень значимости p, из соотношения 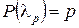мож-но найти соответствующее критическое значение 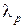. В таблице 8 приводятся критические значения 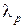критерия Колмогорова для некоторых p.

Таблица 8

Критические значения 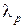критерия Колмогорова

для некоторых p

Уровень значимости p	0,40	0,30	0,20	0,10	0,05	0,025	0,01	0,005	0,001	0,0005
Критическое значение	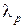0,89	0,97	1,07	1,22	1,36	1,48	1,63	1,73	1,95	2,03

Таблица 8

таблица значений вероятностей для критерия Пирсона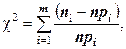

k	Значения c ^2 в зависимости от k и р
0,99	0,98	0,95	0,90	0,80	0,70	0,50	0,30	0,20	0,10	0,05	0,02	0,01	0,001
	0,000	0,001	0,004	0,016	0,064	0,148	0,455	1,074	1,642	2,71	3,84	5,41	6,64	10,83
	0,020	0,040	0,103	0,211	0,446	0,713	1,386	2,41	3,22	4,60	5,99	7,82	9,21	13,82
	0,115	0,185	0,352	0,584	1,005	1,424	2,37	3,66	4,64	6,25	7,82	9,84	11,34	16,27
	0,297	0,429	0,711	1,064	1,649	2,20	3,36	4,88	5,99	7,78	9,49	11,67	13,28	18,46
	0,554	0,752	1,145	1,610	2,34	3,00	4,35	6,06	7,29	9,24	11,07	13,39	15,09	20,5
	0,872	1,134	1,635	2,20	3,07	3,83	5,35	7,23	8,56	10,64	12,59	15,03	16,81	22,5
	1,239	1.564	2,17	2,83	3,82	4,67	6,35	8,38	9,80	12,02	14,07	16,62	18,48	24,3
	1,646	2,03	2,73	3,49	4,59	5,53	7,34	9,52	1,03	13,36	15,51	18,17	20,1	26,1
	2,09	2,53	3,32	4,17	5,38	6,39	8,34	10,66	12,24	14,68	16,92	19,68	21,7	27,9
	2,56	3,06	3,94	4,86	6,18	7,27	9,34	11,78	13,44	15,99	18,31	21,2	23,2	29,6
	3,05	3,61	4,58	5,58	6,99	8,15	10,34	12,90	14,63	17,28	19,68	22,6	24,7	31,3
	3,57	4,18	5,23	6,30	7,81	9,03	11,34	14,01	15,81	18,55	21,0	24,1	26,2	32,9
	4,11	4,76	5,89	7,04	8,63	9,93	12,34	15,12	1б,98	19,81	22,4	25,5	27,7	34,6
	4,66	5,37	6,57	7,79	9,47	10,82	13,34	16,22	18,15	21,1	23,7	26,9	29,1	36,1
	5,23	5,98	7,26	8,55	10,31	11,72	14,34	17,32	19,31	22,3	25,0	28,3	30,6	37,7
	5,81	6,61	7,96	9,31	11,15	12,62	15,34	18,42	20,5	23,5	26,3	29,6	32,0	39,3
	6,41	7,26	8,67	10,08	12,00	13,53	16,34	19,51	21,6	24,8	27,6	31,0	33,4	40,8
	7,02	7,91	9,39	10,86	12,86	14,44	17,34	20,6	22,8	26,0	23,9	32,3	34,8	42,3
	7,63	8,57	10,11	11,65	13,72	15,35	18,34	21,7	23,9	27,2	30,1	33,7	36,2	43,8
	8,26	9,24	10.85	12,44	14,58	16,27	19,34	22,8	25,0	28,4	31,4	35,0	37,6	45,3
	8,90	9,92	11,59	13,24	15,44	17,18	20,3	23,9	26,2	29,6	32,7	36,3	38,9	46,8
	9,54	10,60	12,34	14,04	16,31	18,10	21,3	24,9	27,3	30,8	33,9	37,7	40,3	48,3
	10,20	11,29	13,09	14,85	17,19	19,02	22,3	26,0	28,4	32,0	35,2	39,0	41,6	49,7
	10,86	11,99	13,85	15,66	18,06	19,94	23,3	27,1	29,6	33,2	36,4	40,3	43,0	51,2
	11,52	12,70	14,61	16,47	18,94	20,9	24,3	28,2	30,7	34,4	37,7	41,7	44,3	52,6
	12,20	13,41	15,38	17,29	19,82	21,8	25,3	29,2	31,8	35,6	38,9	42,9	45,6	54,1
	12,88	14,12	16,15	18,11	20,7	22,7	26,3	30,3	32,9	36,7	40,1	44,1	47,0	55,5
	13,56	14,85	16,93	18,94	21,6	23,6	27,3	31,4	34,0	37,9	41,3	45,4	48,3	56,9
	14,26	15.57	17,71	19,77	22,5	24,6	28,3	32,5	35,1	39,1	42,6	46,7	49,6	58,3
	14,95	16,31	18,49	20.6	23,4	25,5	29,3	33,5	36,2	40,3	43,8	48,0	50,9	59,7

Схема применения критерия Колмогорова следующая:

1. Строятся эмпирическая функция распределения F_n(x ) и предполагаемая теоретическая функция распределения F(x ).

2. Определяется мера расхождения между теоретическим и эмпирическим распределением D по формуле

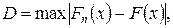
и вычисляется величина .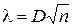

3. Если вычисленное значение 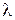окажется больше критическо-го 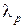, определённого на уровне значимости p, то гипотеза о том, что случайная величина X имеет заданный закон распределения, отвергается. Если 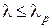, то считают, что гипотеза не противоречит опытным данным.

Критерий Колмогорова достаточно часто применяется на практике благодаря своей простоте. Однако в принципе его применение возможно лишь тогда, когда теоретическая функция распределения F(x) задана полностью. Но такой случай на практике встречается весьма редко. Обычно из теоретических соображений известен лишь вид функции распределения, а её параметры определяются по эмпирическим данным. При применении критерия 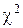это обстоятельство учитывается соответствующим уменьшением числа степеней свободы. Такого рода поправок в критерии Колмогорова не предусмотрено. Поэтому, если при неизвестных значениях параметров применить критерий Колмогорова, взяв за значения параметров их оценки, то получим завышенное значение вероятности 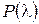, а значит, большее критическое значение 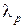. В результате есть риск в ряде случаев принять гипотезу о законе распределения случайной величины как правдоподобную, в то время как на самом деле она противоречит опытным данным.

Дата добавления: 2014-01-04