
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Числовые функции
|
|
|
|
Исследование функций с помощью производных
Дифференциальное исчисление функции одной переменной
Числовые функции. Пределы. Непрерывность
Понятие числовых функций…….…………………………………………4
Предел числовой функции…………………………………………………5
Основные теоремы о пределах…………………………………………….8
Бесконечно малые и бесконечно большие функции……………………..9
Сравнение асимптотического поведения функций……………………..11
Непрерывность функции в точке и на множестве………………………13
Точки разрыва функции и их классификация их………………………..15
Действия над непрерывными функциями. Непрерывность основных
элементарных функций…………………………………………………..16
Свойства функций, непрерывных на отрезке……………………………18
Понятие производной. Механический и геометрический смысл
производной……………………………………………………………… 22
Дифференцируемость функции…………………………………………..28
Дифференциал функции……….………………………………………….30
Производная сложной функции …………………………………………32
Дифференциал сложной функции. Инвариантность формы
дифференциала…………………………………………………………… 33
Правила дифференцирования …………………………………………… 34
Логарифмическое дифференцирование………………………………….36
Производная обратной функции…………………………………………. 37
Производные высших порядков…………………………………………..38
Дифференцирование неявно заданных функций…………………………39
Дифференцирование функций, заданных параметрически……………. 40
Дифференциалы высших порядков……………………………………….42
Теоремы о среднем значении……………………………………………..44
Правило Лопиталя…………………………………………………………49
Возрастание и убывание функции………………………………………..51
Точки локального экстремума функции. Необходимое и достаточные
условия существования экстремума функции………............................ 53
Необходимое условие существования экстремума функции………….. 54
Достаточные условия существования экстремума………………………55
Исследование функции на выпуклость и вогнутость
Точки перегиба функции…………………………………………………. 58
Асимптоты графика функции……………………………………………..60
Общая схема исследования функции……………………………………. 63
Литература………………………………………………………..…………68
Определение. Пусть 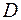 произвольной подмножество действительных чисел. Однозначной числовой функцией
произвольной подмножество действительных чисел. Однозначной числовой функцией 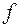 , определенной на множестве называется закон, по которому каждому числу
, определенной на множестве называется закон, по которому каждому числу  поставлено в соответствие одно действительное число
поставлено в соответствие одно действительное число  .
.
Множество 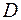 при этом называется областью определения функции, а множество
при этом называется областью определения функции, а множество  — множеством значений функции.
— множеством значений функции.
В дальнейшем мы будем рассматривать только однозначные функции.
Пусть на некотором множестве 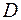 определена числовая функция
определена числовая функция 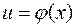 и
и 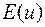 — множеством значений функции. Пусть на множестве
— множеством значений функции. Пусть на множестве 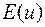 задана функция (
задана функция (
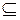
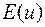 ). Тогда функция
). Тогда функция 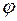 отображает элементы
отображает элементы  в элементы
в элементы  , а функция
, а функция 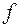 отображает элементы
отображает элементы  в элементы
в элементы  ,
,
|
|
|
|
Дата добавления: 2014-01-04; Просмотров: 330; Нарушение авторских прав?; Мы поможем в написании вашей работы!