Непрерывность функции в точке и на множестве

Интуитивное представление о непрерывной функции обычно связывают с такой функцией, график которой — непрерывная линия.

Определение 1. Функция называется непрерывной в точке , если выполняются следующие три условия:

1) функция определена в точке , т. е. ;

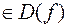2) существует ;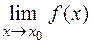

3) .

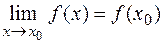Если в точке нарушено хотя бы одно из условий 1—3, то функция называется разрывной в точке , а точка — точкой разрыва.

Если воспользоваться определением предела функции в точке по Коши, то можно дать эквивалентное определение непрерывной функции в точке на языке «— ».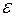

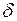Определение 2. Функция называется непрерывной в точке , если для любого заданного числа 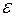> 0 можно найти такое число 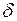> О (зависящее от 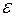и ), что для всех , для которых 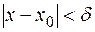, будет выполняться неравенство .

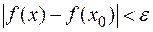В более краткой записи определение можно записать так:

непрерывна в точке

.

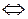
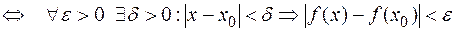Так как 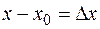— приращение аргумента, a 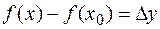— приращение функции в точке , то определение 2 можно сформулировать следующим образом: функция непрерывна в точке , если 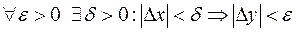, т.е. 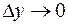при 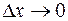. Таким образом, получаем еще одно определение непрерывности.

Определение 3. Функция называется непрерывной в точке , если бесконечно малому приращению аргумента 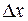соответствует бесконечно малое приращение функции , т. е. .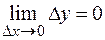

В некоторых случаях приходится пользоваться понятием односторонней непрерывности.

Определение. Функция , определенная в некоторой левой (правой) окрестности точки , называется непрерывной слева (справа) в точке , если существует предел слева (справа) функции и он равен .

Другими словами,

непрерывна справа в точке ,

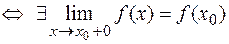непрерывна слева в точке .

Из определения односторонней непрерывности в точке следует, что функция , определенная в некоторой 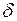-окрестности точки , непрерывна в точке тогда и только тогда, когда она непрерывна в этой точке слева и справа.

Определение. Функция , непрерывная во всех точках некоторого множества X, называется непрерывной на этом мно­жестве.

Если X = , то для непрерывности функции на требуется, чтобы была непрерывна во всех внутренних точках отрезка, непрерывна справа на левом его конце, т. е. в точке а, и непрерывна слева на правом его конце, т. е. в точке b.

Точки разрыва функции и их классификация

Если хотя бы одно из условий определения 1 не выполнено, то точка является точкой разрыва. Различают следующие виды точек разрыва:

1) если 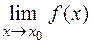существует, но функция в точке не определена или определена, но то точка называется точкой устранимого разрыва;

2) если существуют конечные односторонние пределы в точке , но они не равны друг другу, то точка называется точкой разрыва первого рода, а модуль разности 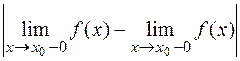— скачком функции в точке ;

3) если хотя бы один из односторонних пределов равен ¥ или вообще не существует, то точка называется точкой раз­рыва второго рода.

Таким образом, при исследовании функции на непрерывность необходимо проверить выполнение условий определения 1. Если — точка разрыва, то для установления характера разрыва не­обходимо вычислить односторонние пределы.

Пример. Исследовать на непрерывность функцию .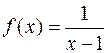

Решение. Область определения данной функции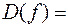(–¥;1)Ç(1; +¥).

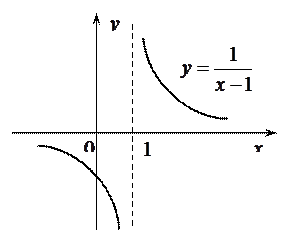Следовательно, является точкой разрыва. Определим характер точки разрыва. Так как

–¥, +¥,

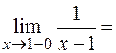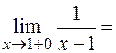то является точкой разрыва второго рода.

Пример. Исследовать на непрерывность функцию

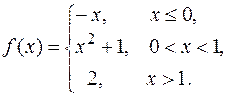
Решение. Так функции , и 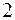непрерывны в области задания, то точками разрыва могут быть только точки перехода от одного аналитического выражения к другому. Исследуем функцию на непрерывность в этих точках.

1) Исследуем функцию в точке . Вычислим односторонние пределы

,

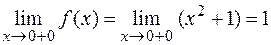
Так как односторонние пределы существуют, конечны, но не равны друг другу, то точка является точкой разрыва первого рода. Модуль разности между левым и правым пределом есть скачок. В данном случае скачок равен 1.

2) Исследуем функцию в точке 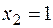. Вычислим односторонние пределы

,

,

,

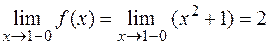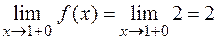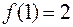То есть, . Следовательно, функция в точке 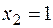непрерывна.

Дата добавления: 2014-01-04