КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Логарифмическое дифференцирование
|
|
|
|
Решение..
Пусть функция 
дифференцируема на отрезке 
и 
>0 для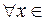 
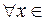
. Тогда определен 
. Рассматривая 
как сложную функцию аргумента 
, принимая за промежуточный аргумент. Применяя правило дифференцирования сложной функции, получим
,
откуда
.
Производную от логарифма функции называют логарифмической производной. Данный метод используется, если производная от логарифма находится легче, чем производная самой функции.
Логарифмическое дифференцирование удобно применять, когда требуется найти производную большого числа сомножителей и производную степенно-показательной функции.
Пример. Найти производную функции 
.
Решение. Найдем 
,
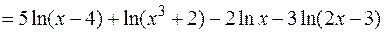Откуда
.
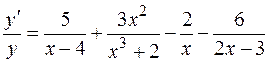
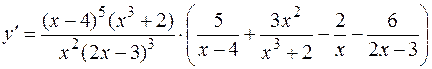Пример. Найти производную функции 
.
Решение. Найдем 
|
|
|
|
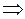
Дата добавления: 2014-01-04; Просмотров: 295; Нарушение авторских прав?; Мы поможем в написании вашей работы!