
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Основные свойства определенного интеграла
|
|
|
|
Рассмотрим свойства определенного интеграла, доказательство которых основывается на определении определенного интеграла.
1. Если нижний и верхний пределы интегрирования равны (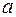 =
= 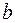 ), то интеграл равен нулю:
), то интеграл равен нулю:
2. Если  = 1, то
= 1, то

3. При перестановке пределов интегрирования определенный интеграл меняет знак на противоположный:
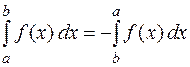
4. Постоянный множитель можно выносить за знак определенного интеграла:
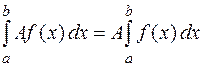 .
.
5. Определенный интеграл от алгебраической суммы конечного числа интегрируемых на  функций
функций  равен алгебраической сумме определенных интегралов от слагаемых:
равен алгебраической сумме определенных интегралов от слагаемых:  .
.
6( Аддитивность определенного интеграла). Если существуют интегралы 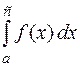 и
и  , то существует также интеграл
, то существует также интеграл 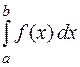 и для любых чисел
и для любых чисел 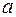 ,
, 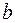 ,
, 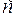
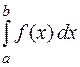
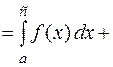
 .
.
Геометрический смысл свойства 6 состоит в том, что площадь криволинейной трапеции с основанием  равна сумме площадей криволинейных трапеций с основаниями
равна сумме площадей криволинейных трапеций с основаниями 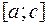 и
и  .
.

7. Если  r0 для
r0 для 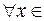
 , то
, то
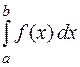 r0, (
r0, ( )
)
8 (Монотонность определенного интеграла). Если интегрируемые функции  и
и 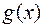 удовлетворяют неравенству
удовлетворяют неравенству  r
r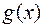 для
для 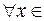
 , то
, то
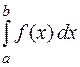 r
r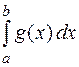 , (
, ( )
)
9 (Об оценке определенного интеграла). Если 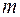 и
и  — соответственно наименьшее и наибольшее значения функции
— соответственно наименьшее и наибольшее значения функции  , непрерывной на отрезке
, непрерывной на отрезке  , то
, то
 b
b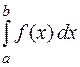 b
b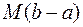 . (1)
. (1)
Доказательство. По условию 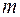 b
b b
b для
для 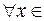
 , следовательно, по свойству 8
, следовательно, по свойству 8
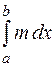 b
b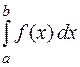 b
b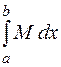
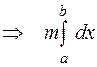 b
b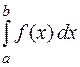 b
b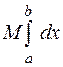 ,
,
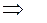
 b
b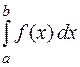 b
b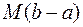 .
.
⊠
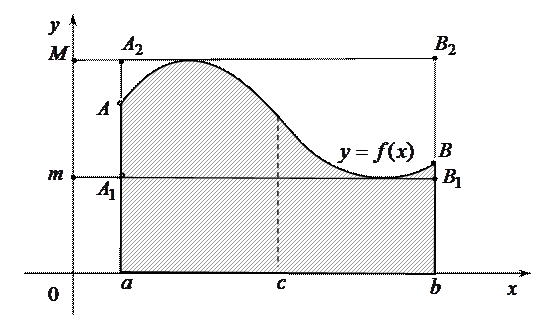
На рисунке дана геометрическая интерпретация свойства 9 в случае, когда  r0
r0 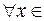
 . Площадь прямоугольника
. Площадь прямоугольника  равна
равна  , площадь прямоугольника
, площадь прямоугольника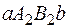 равна
равна 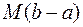 . Из неравенства (1) следует, что площадь криволинейной трапеции
. Из неравенства (1) следует, что площадь криволинейной трапеции  не меньше площади первого прямоугольника и не больше площади второго.
не меньше площади первого прямоугольника и не больше площади второго.
10 (Теорема о среднем). Если функция  непрерывна на отрезке
непрерывна на отрезке  , то существует такая точка
, то существует такая точка 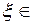
 , что
, что
 . (2)
. (2)
т. е. определенный интеграл от непрерывной функции равен произведению значения подынтегральной функции в некоторой промежуточной точке отрезка интегрирования  и длины
и длины  этого отрезка.
этого отрезка.
Доказательство. Так как непрерывна на отрезке
непрерывна на отрезке  , то она по теореме Вейерштрасса достигает на
, то она по теореме Вейерштрасса достигает на  своего наименьшего
своего наименьшего 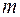 и наибольшего
и наибольшего  значений, т. е.
значений, т. е.
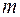 b
b b
b для
для 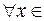
 .
.
Из данного неравенства на основании свойства 9 имеем
 b
b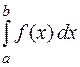 b
b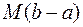 .
.
Разделив все члены двойного неравенства на  > 0, получим
> 0, получим
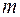 b
b b
b
Обозначим 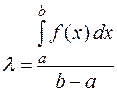 , тогда
, тогда 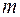 b
b b
b .
.
Другими словами, число  находится между наименьшим и наибольшим значениями функции
находится между наименьшим и наибольшим значениями функции  . Поскольку непрерывная на отрезке
. Поскольку непрерывная на отрезке  функция
функция  по теореме Больцано-Коши принимает все промежуточные значения, лежащие между
по теореме Больцано-Коши принимает все промежуточные значения, лежащие между 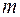 и
и  , в том числе и значение
, в том числе и значение  , то существует
, то существует 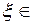
 , такое, что
, такое, что  =
=  , то есть
, то есть

 ,
, 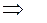
 .
.
⊠
Число  при этом называется интегральным средним значением функции
при этом называется интегральным средним значением функции  на отрезке
на отрезке  .
.
На рисунке дана геометрическая интерпретация свойства 10 в случае, когда  > 0
> 0 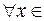
 . Так как значение
. Так как значение  (
( ) численно равно площади прямоугольника с основанием
) численно равно площади прямоугольника с основанием  и высотой
и высотой  , то теорема о среднем утверждает, что существует прямоугольник, равновеликий криволинейной трапеции
, то теорема о среднем утверждает, что существует прямоугольник, равновеликий криволинейной трапеции  .
.

|
|
|
|
Дата добавления: 2014-01-04; Просмотров: 747; Нарушение авторских прав?; Мы поможем в написании вашей работы!