Погрешность суммы

Частные случаи

Пусть зависимость Y от X_i имеет вид суммы:

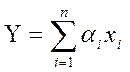
Частные производные

Абсолютная систематическая погрешность

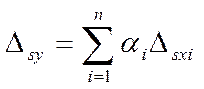
Для некореллированных погрешностей

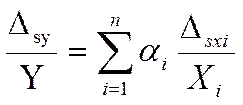
3.6. Правила проверки согласия опытного распределения случайной величины с теоретическим.

До сих пор мы считали, что случайные погрешности распределены по нормальному закону, и в соответствии с этим строили методы обработки результатов.

Как отмечалось, хотя в большинстве случает измерения физических величин предположение о нормальности оправдано, бывает необходимо проверить, а так ли это в данной конкретной ситуации.

Это можно выполнить путем построения так называемой гистограммы. Анализ ее формы позволяет выдвинуть гипотезу о предполагаемой закономерности распределения случайной величины. Степень соответствия между выдвинутой гипотезой и результатами наблюдений устанавливается с помощью критерия согласия.

Остановимся более подробно на методике построения гистограммы - графического представления распределения результатов измерения (их случайных отклонений).

Гистограмма - это график распределения результатов ограниченного количества измерений (n>30…50) одной и той же величины.

Графическое представление результатов большого числа измерений (n) - это кривая предельной функции распределения (например, нормального закона Гаусса, равномерный закон, треугольный закон распределения Симпсона, закон Релея и т.д.).

Допустим, произведено n-число (n>30) измерений одной и той же величины одним и тем же оператором, на одном и том же оборудовании и в одних и тех же условиях (такие измерения называются равноточными).

а). Эти значения случайных величин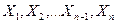

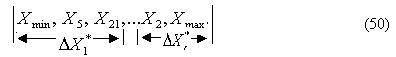б). Этот вариационный ряд значений располагают в порядке возрастания величины слева направо

в). Весь диапазон полученных результатов измерений 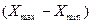разделяют на r интервалов ("бинов") шириной

Ширина равномерных интервалов равна

(51)

Определим границы интервалов

Число интервалов r определяется числом измерений n и может быть выбрана на основании таблицы рекомендованной ВНИИМ

Таблица 8

n	r
< 30 30 - 100 100 - 500 500 - 1000 1000 - 10000	5 - 8 7 - 9 8 - 12 10 - 16 12 - 22

Следует соблюдать некоторую осторожность при выборе ширины бинов для гистограммы. Если бины выбраны слишком широкими, то все (или почти все) отсчеты попадут в один бин и гистограмма выродится в малоинтересный единственный прямоугольник. Если же бины выбраны слишком узкими, то лишь небольшое их число будет содержать более чем один отсчет и сама гистограмма будет состоять из большого числа узких прямоугольников, почти одинаковой высоты. Если распределение крайне неравномерно, то в области максимальной концентрации результатов измерений следует выбирать более узкие интервалы, бины.

Масштабы по осям гистограммы должны быть такими, чтобы отношение ее высоты к основанию составляло примерно 5:8.

г). Подсчитывают частоты 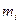, равные числу результатов, лежащих в каждом i-м интервале, т.е. меньших или равных его правой и больших левой границы

Отношение , (52)

где n - общее число наблюдений называется частостями (частость) и представляют собой статистические оценки вероятностей попадания результата измерения в i-й интервал. Распределение частостей по интервалам образуют статистическое распределение результатов измерений.

д). Если теперь разделить частость на длину интервала, то получим величины (53)

являющиеся оценками средней плотности распределения в интервале .

е) Отложим вдоль оси (абсцисс) интервалы в порядке возрастания индекса i и на каждом интервале построим прямоугольник с высотой равной 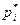. Полученный график называется гистограммой статистического распределения.

Сумма площадей всех прямоугольников равна единице:

Пример: Было выполнено 100 измерений среднего диаметра резьбового калибра. Результаты измерений лежат в диапазоне 8,911 - 8,927 мм, т.е. ширина зоны распределения результатов составляет 0,016 мм. Весь диапазон удобно разделить на восемь равных интервалов (бинов) через 0,002 мм. В таблице приведены частоты частности 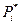и плотности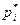статистического распределения

Таблица 9

I
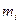
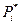
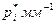
	8,911 8,913 8,915 8,917 8,919 8,921 8,923 8,925	8,913 8,915 8,917 8,919 8,921 8,923 8,925 8,927		0,01 0,05 0,14 0,27 0,24 0,18 0,09 0,02

Математическое окружение результатов измерения 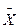=8,91936 мм,

Стандартное отклонение мм

Уравнение кривой нормального распределения

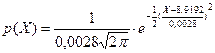
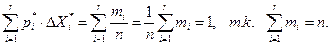(54)

При увеличении числа наблюдений число интервалов можно увеличить, а сами интервалы уменьшить, тогда гистограмма все больше приближается к плавной кривой, ограничивающей единичную площадь - к графику плотность распределения результатов наблюдений описываемой формулой (33). Параметры могут быть вычислены по формулам (39) и (32).

Пример построения гистограммы дан на рис.14.

ЛИТЕРАТУРА

По метрологии:

1. Дворяшин Б.В. Основы метрологии и радиоизмерения. 1993г.

2. Тартаковский Д.Ф., Ястребов А.С. Метрология, стандартизация и технич. средства измерений. М. ВШ. 2001г.

3. Бурдун Г.Д. и др. Основы метрологии. 1985г.

4. Вяселев М.Р. Основы метрологии РЭА, КАИ. 1986г.

5. Под. ред. Душина Е.М. (Авдеев Б.Я. и др.) Основы метрологии и электрич. Измерения. Л. 1987г.

6. Атамалян Э.Г. Приборы и методы измерения электрических величин. М. 1989г.

7. Атамалян Э.Г. и др. Методы и средства измерения электрических величин. М. 1974г.

По средствам и методам измерения:

1. п. 5, 6, 7 из литературы по метрологии

2. Кукуш В.Д. Электрорадиоизмерения. М. 1985г.

3. Винокуров В.И. и др. Электрорадиоизмерения. М. 1986г.

Дата добавления: 2014-01-04