Броуновское движение

Лекция 3.Молекулярно-кинетические и оптические свойства коллоидных систем.

Броуновское движение.

Диффузия.

Осмотическое давление коллоидных растворов.

Седиментация в дисперсных системах.

Оптические свойства дисперсных систем.

Явление рассеяния света.

Поглощение (адсорбция) света.

Коллоидные частицы по молекулярно-кинетическим свойствам принципиально не отличаются от истинных растворов. Взвешенные в растворе частицы находятся постоянном беспорядочном тепловом движении (Броуновское движение – открыл в 1827 году английский ботаник Р.Броун, наблюдая как микроскопические частицы пыльцы и спор непрерывно и хаотично передвигаются в воде). При столкновении частиц происходит обмен количеством энергии и в результате устанавливается средняя кинетическая энергия, одинаковая для всех частиц. Молекулы (например, газа) движутся со скоростью сотни метров в секунду, коллоидные частицы размером 3-5 мкм - доли миллиметров в секунду, что обусловлено их гигантскими размерами.

Траектория движения частиц, зафиксированная с помощью кинематографической микросъемки имеет вид ломаной линии (рис. 3.1).

Рис. 3.1. Схема перемещения частицы при

броуновском движении.

Средняя квадратичная величина всех смещений без учета направления движения равна:

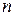- число смещений (число отрезков ломаной линии);

- отдельные проекции смещения частицы на ось х.

Элементарные исследования броуновского движения проводились Р. Зигмонди, Ж. Перреном, Т. Сведбергом, а теория этого движения была развита Эйнштейном и Смолуховским (1905).

Уравнеие Эйнштейна-Смолуховского для среднего квадратичного смещения частицы за время t при броуновском движении имеет вид:

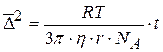
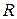- универсальная газовая постоянная;

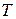- абсолютная температура;

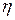- вязкость среды;

- радиус взвешенных частиц;

- постоянная Авогадро;

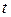- время.

Из уравнения следует вывод – чем крупнее частица, тем меньше величина ее смещения.

Кроме поступательного движения частицы обладают также и вращательным движением.

Для вращательного броуновского движения частиц сферической формы среднее квадратичное значение угла вращения (угла поворота) составит:

Теория Эйнштейна получила многочисленные и неоспоримые доказательства.

Например, блестящим подтверждением теории являлись работы Ж. Перрена, который в своих опытах использовал сферические частицы мастики с точно известным радиусом 1 мкм. Измеряя на этом золе поступательное и вращательное движение частиц при известных значениях Т и h Перрен вычислил постоянную Авогадро N_A=6,5×10²³.

Дата добавления: 2014-01-04