Механизмов

ПОСТАНОВКА ЗАДАЧИ ОПТИМАЛЬНОГО ПРОЕКТИРОВАНИЯ

Новосибирск 2003

КОНСПЕКТ

лекций по курсу «Поисковые методы оптимального проектирования»

для студентов направления 651600 «Технологические машины

и оборудование» и специальности 170700 «Машины и аппараты

текстильной и легкой промышленности»

Разработчик доц., к.т.н. Ермолаев В.Ф.

Рецензент проф., д.т.н. Подгорный Ю.И.

Работа выполнена на кафедре механики НТИ МГУДТ (филиал)

Под оптимальным проектированием понимается процесс принятия наилучших (оптимальных) в некотором смысле решений с помощью ЭВМ.

Общим для задач оптимального проектирования механизмов является то, что они математически формулируются как задача нелинейного программирования. При этом предполагается, что имеется математическая модель механизма и требуется для заданной модели найти такие параметры, которые обеспечивают экстремальное значение одной из наиболее важных характеристик механизма при условии, что другие удовлетворяют заданной системе ограничений.

Задача создания наилучших машин и механизмов до настоящего времени не имеет однозначного решения. Несмотря на то, что задача оптимального проектирования механизмов позволяет удовлетворять тем требованиям, которые определяются технологией и надежностью проектируемых механизмов, она продолжает формулироваться как задача наилучшего приближения функций. Это в какой-то степени снижает эффективность спроектированных механизмов, так как необходимая передаточная функция проектируемого механизма или необходимая траектория движения какой-либо точки звена механизма являются, как правило, неизвестными. Они выбираются из интуитивных соображений, чаще всего основанных на опыте или традициях.

Как и любая задача, задача оптимального проектирования механизмов состоит из двух частей: постановки задачи и её решения. Корректная постановка задачи оптимального проектирования механизмов не менее сложна и безусловно имеет первостепенное значение. По этим причинам изложение материала сопровождается большим количеством примеров, построенных автором на основе собственного инженерного опыта.

Для решения на ЭВМ задачи оптимального проектирования механизмов необходимо иметь их математические модели. Несмотря на всю сложность и разнообразие кинематических схем механизмов (механизмы с низшими и высшими кинематическими парами, с силовым или кинематическим замыканием кинематических пар и т.п.) процесс построения математической модели механизма содержит следующие общие этапы:

- формализация задачи проектирования;

- анализ и выделение существенных показателей и характеристик механизма;

- построение математического описания, отражающего взаимосвязь показателей и характеристик механизма от его параметров;

- проведение экспериментальных исследований для определения соответствия математической модели реальным условиям.

Исходной информацией при этом являются требования технологического процесса, условия эксплуатации и режимы работы проектируемой машины и механизма. Анализ полученных данных позволяет определить основную цель проектирования механизма и формализовать требования, предъявляемые к проектируемому механизму. Необходимо отметить, что целевое назначение механизма и цель его оптимального проектирования, это разные понятия. Механизмы должны выполнять те целевые функции, т.е. технологические операции, ради которых они создаются. Целью же оптимального проектирования механизма может являться повышение производительности труда, снижение себестоимости продукции, получение минимального веса или минимальных габаритов, максимальная долговечность, улучшение качественных характеристик технологического процесса и т.д.

Существующие методы оптимального проектирования позволяют решать задачу оптимизации при наличии одного критерия оптимальности. Задачи, стоящие перед конструктором, как правило, многоцелевые. Например, при получении скоростного максимального режима механизма обеспечить минимальные динамические нагрузки; при получении максимальной производительности обеспечить минимальную стоимость механизма или машины в целом. Это противоречивые или конкурирующие цели: при повышении скоростного режима увеличиваются динамические нагрузки, при повышении производительности, как правило, увеличивается сложность, а следовательно и стоимость, механизма. При наличии конкурирующих целей требуется найти компромиссное решение так, чтобы получить один критерий оптимальности. Для этого имеется несколько путей.

Первый путь: сконструировать сложный, комплексный критерий оптимальности. Например, оптимальным считать такой механизм, который обеспечивает максимальное значение функции

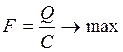, (1)

где Q – производительность, С – стоимость.

Из формулы (1) видно, что критерий оптимальности будет возрастать и при увеличении производительности, и при уменьшении стоимости, но он может возрастать и при одновременном увеличении производительности и стоимости. Не всегда удается найти комплексный критерий, имеющий четкий физический смысл.

Второй путь: выбрать в качестве цели оптимального проектирования один из показателей, а на остальные наложить ограничения. Например, производительность механизма должна быть максимальной, а стоимость не должна превышать определенной величины; скоростной режим должен быть максимальным, а реакции в кинематических парах не должны превышать допустимых значений. При таком подходе задача всегда сохраняет четкий физический смысл.

Третий путь: многокритериальное проектирование без свертки всех критериев в один [8]. В такой постановке задача решается в интерактивном режиме. Интерактивный режим предполагает возможность оперативного взаимодействия конструктора с ЭВМ на любом этапе решения задачи. Для того чтобы полностью использовать возможности интерактивного режима при решении задачи оптимального проектирования механизмов необходимо выполнение ряда условий, таких как создание САПР и соответствующая подготовка конструкторов.

В дальнейшем постановка задачи оптимального проектирования механизмов осуществляется по второму пути.

Предположим, что критерий оптимальности и ограничения выбраны. Теперь следует построить математическую модель критерия оптимальности, т.е. необходимо получить математическую зависимость (в явном или неявном виде) критерия оптимальности от варьируемых (определяемых) параметров механизма. Эта зависимость называется целевой функцией

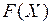, (2)

где 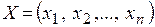- множество варьируемых в процессе проектирования механизма параметров: размеры звеньев, массы звеньев, координаты центров тяжести звеньев, жесткостные и инерционные характеристики и т.д.

Задача состоит в том, чтобы найти множество 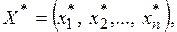т.е. такие значения варьируемых параметров, чтобы целевая функция обращалась в минимум или максимум. Варьируемые параметры не могут принимать произвольные значения, а могут изменяться только в каких-то пределах, определяемых ограничениями на проектирование. Таким образом 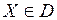, где множество D определяется системой m равенств или неравенств, представляющих собой математические модели ограничений на проектирование:

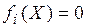(i = 1,2,…,), (3)

(j = ). (4)

Теперь можно полностью сформулировать задачу оптимального проектирования механизмов: найти на множестве D такое множество варьируемых параметров 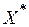, чтобы

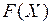. (5)

Задача максимизации целевой функции сводится к (5), если принять

,

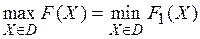где .

2 ПРИМЕРЫ СОСТАВЛЕНИЯ ЦЕЛЕВЫХ ФУНКЦИЙ

2.1 Оптимальное проектирование механизмов универсальной

швейной машины

Дата добавления: 2014-01-04