Рассмотрим различные случаи применения записанных выше уравнений для расчёта канала

Решая уравнение (10) относительно c ₁, находим:

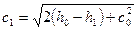, (12)

где h – энтальпия, Дж/кг, а c – скорость, м/с.

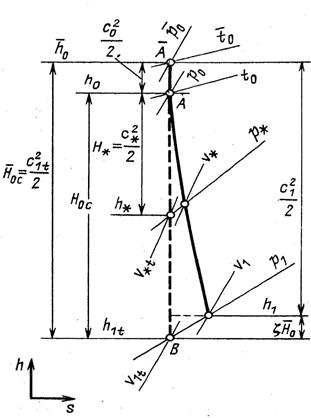
Рис. 2

Энтальпию h ₀ рабочего тела можно найти непосредственно из h,s – диаграммы (рис. 2). Если энтальпия h ₁ в конце процесса расширения также задана, то по формуле (12) можно найти скорость c ₁

При изоэнтропном расширении (линия А – В) можно найти h _1t, и следовательно скорость c _1t.

Канал, в котором поток плавно ускоряется, называется сопловым или соплом.

Согласно формуле (8) можно найти скорость c _1t:

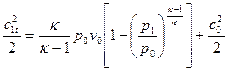. (13)

Если начальной кинетической энергией потока 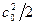пренебречь нельзя, то можно предположить, что она возникла в результате изоэнтропийного расширения рабочего тела от некоторых фиктивных параметров 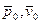, при которых начальная скорость равнялась нулю, до параметров перед соплом 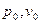. Иными словами, параметры 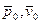возникнут в том случае, если поток текущий со скоростью c ₀ изоэнтропийно затормозится до нулевой скорости.

Отсюда принято называть параметры 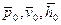параметрами изоэнтропийного заторможенного потока, или параметрами торможения.

Тогда:

, (14)

где 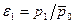- отношение давления p ₁ к давлению заторможенного потока .

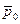Давления p ₀ и p ₁ в отличии от давления заторможенного потока называются статическими.

Параметры торможения можно найти при помощи h,s – диаграммы (рис. 2). Откладывая по изоэнтропе отрезок 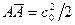от точки, соответствующей начальным параметрам p ₀ и t ₀, находим в точка 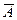параметры заторможенного потока .

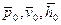Если скорость c ₀ невелика и не превышает 100 – 150 м/с, то для определения параметров торможения удобно пользоваться следующими приближёнными формулами:

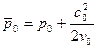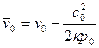; . (15)

Учитывая, что распространение звука происходит со скоростью:

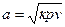, (16)

можно, преобразовав формулу (13) с учётом (14), привести её к виду:

, (17)

где a ₁ – скорость звука при параметрах рабочего тела p ₁, v ₁; 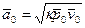- скорость звука при параметрах торможения.

Если скорость потока в процессе расширения достигнет скорости звука c ₁= a ₁= a _*, то такую скорость и соответствующие ей параметры называют критическими и обозначаются звёздочкой.

Критическое отношение давления при c _1t =a _1t =a _* равно:

, (18)

а критическая скорость потока:

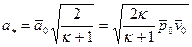. (19)

В анализе процесса течения рабочего тела широко используются безразмерные скорости:

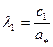
и число Маха .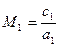

При критическом отношении давлений ε_* безразмерные скорости равны единице:

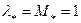
Если определить, как должна меняться площадь сечения сопла по мере расширения рабочего тела, то для изоэнтропного процесса расширения получим зависимость, представленную на рис. 3.

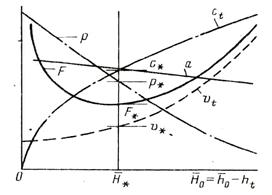
Рис. 3

Для этого возьмём несколько промежуточных точек на изоэнтропе А – В (рис. 2) и, подсчитав по найденным уравнениям скорости и площади сечения, построим соответствующие зависимости. На рис. 3 представлена диаграмма изменения параметров рабочего тела p и v, скорости потока с₁ и площади поперечного сечения сопла F в зависимости от изоэнтропного теплоперепада H₀. Кривая F показывает, что при определённой величине теплоперепада площадь сечения сопла имеет минимум F_* и что дальнейшее расширение рабочего тела требует постепенного увеличения площади сечения F.

При изоэнтропном течении минимальное сечение сопла, а также параметры рабочего тела, которые соответствуют этому сечению, совпадают с критическими, т.е. скорость потока c_t в минимальном сечении сопла достигает скорости распространения скорости звука a и c_t = a = a_*. Используя уравнение неразрывности, находим

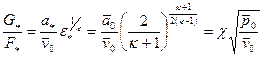, (20)

где G_* - критический расход рабочего тела, кг/с;

F_* - площадь канала в критическом сечении, м²;

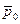- давление торможения, Па;

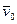- удельный объём рабочего тела при давлении торможения, м³/кг;

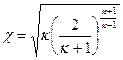- коэффициент, зависящий от показателя к.

Приведённый (относительный) расход выраженный в долях критического, равен:

.

Рис.4

Полученные зависимости представлены на диаграмме рис. 4, на котором видно, что для потока сжимаемой жидкости характерны две области:

· область дозвукового течения в пределах изменения ε от 1 до ε_*;

· сверхзвуковая область в пределах изменения ε от ε_* до 0.

Для того чтобы понять причину, вызывающую сокращение площади поперечного сечения F в докритической зоне и рост её в сверхзвуковой области, используем уравнение неразрывности в дифференциальной форме (5):

.

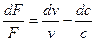Это выражение показывает, что приращение площади сечения канала имеет отрицательное или положительное значение в зависимости от того, какое из слагаемых правой части равенства больше по абсолютной величине.

Так, если в докритической области величина dc/c превышает dv/v, что приводит к отрицательному dF/F, т.е. к уменьшению площади проходного сечения, то при переходе в сверхкритическую область приращение объёма рабочего тела в процессе расширения начинает преобладать над приращением скорости потока и проходное сечение канала увеличивается.

Необходимость перехода к расширяющимся соплам при сверхкритическом расширении рабочего тела было установлено Лавалем, который впервые применил расширяющиеся сопла в своей турбине, поэтому такие сопла получили название соплами Лаваля.

Дата добавления: 2014-01-04