Расширение рабочего тела в косом срезе решётки

Рассмотрим сверхзвуковое истечение рабочего тела в суживающейся решётке. При М_1t=1, т.е. при 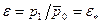, в минимальном выходном сечении решётки АС (рис. 16) устанавливается критическое давление и скорость с _*.

Рис. 16

При уменьшении р ₁ ниже р _* расширение рабочего тела до давления р _* в сечении АС до более низкого давления р ₁ будет происходить уже не в суживающемся канале решётки, а внутри косого среза (в зоне ABC). При этом очевидно, что в точке А давление должно понижаться от р _* до р ₁, т.е. в этой точке возникает возмущение потока. Это возмущение распространяется в движущейся среде со скоростью звука, и расположение изобар в пределах косого среза будет определяться линиями, проведёнными из точки А.

Направление потока рабочего тела, выходящего из решётки, перестаёт совпадать с нормалью к прямой АВ (угол наклона этой нормали условно можно принять равным α_1э) и весь поток отклоняется на угол δ от направления α_1э, т.е..

В том случае, когда расширение рабочего тела происходит в пределах косого среза, угол отклонения потока рабочего тела при выходе из решётки может быть приближённо найден из уравнения неразрывности.

Приравнивая между собой расходы рабочего тела в критическом сечении и на срезе сопла решётки и приняв μ₁=μ_* и l ₁^”= l ₁, получаем:

(37)

или для рабочей решётки

. (38)

Используя уравнения изоэнтропы, формулу (37) можно преобразовать в соотношение:

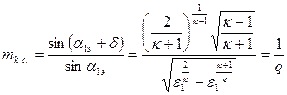. (39)

Из уравнения (39) можно установить зависимость между степенью расширения ε₁ и углом отклонения потока в косом срезе. При некотором отношения давлений ε_α, называемым предельным, полностью исчерпывается расширительная способность косого среза. Это предельное расширение соответствует тому случаю, когда линия постоянного давления, выходящая из точки А (рис. 17), приблизительно совпадает с плоскостью АВ ограничивающей косой срез.

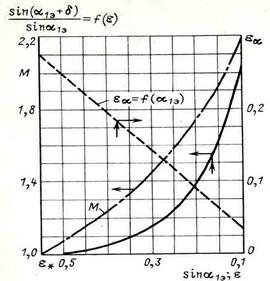
Рис. 17

При ε₁< ε_α расширение рабочего тела будет происходить за пределами косого среза решётки и давления по обводу профиля не будут меняться и, как следствие этому, усилие R_u, действующее на профиль в окружном направлении, останется неизменным.

Таким образом, при ε₁< ε_α вплоть до ε→0 окружная составляющая скорости c ₁ cos α ₁ , достигнув наибольшей величины, будет оставаться неизменной, что показано на годографе скорости на рис.18:

Рис. 18

Поскольку понижение давления за решёткой не будет передаваться вверх по потоку в косой срез решётки, начиная с 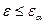, этому режиму ε_α должна соответствовать осевая скорость, равная скорости звука а, т.е.

.

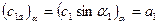Отсюда легко получить выражение для угла поворота α_1α и отношения давлений ε_α при режиме предельного расширения в косом срезе решётки:

.

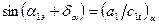Предельная степень расширения ε_α в зависимости от угла α_1э показана пунктирной линией на рис. 17 и её можно определить из выражения:

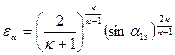. (40)

Дата добавления: 2014-01-04