Преобразование энергии в осевой турбинной ступени

Турбинная ступень

Лекция № 7

В ступени турбины работа расширения рабочего тела преобразуется в кинетическую энергию потока, а последняя – в механическую работу. Рассмотрим это преобразование применительно к одной из ступеней осевой турбины

.

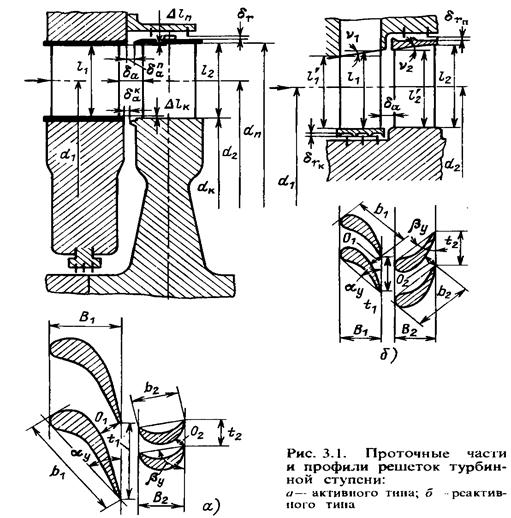
Рис. 24

На рис. 24 показаны проточные части и профили решёток турбинной ступени: а – ступень активного типа; б – ступень реактивного типа.

Поток рабочего тела, вышедший из сопловой решётки со скоростью с ₁, проходит осевой зазор δ _а, отделяющий неподвижные сопловые лопатки от рабочих, и поступает в каналы рабочей решётки (рис. 25).

Рис. 25

В сопловой решётке рабочее тело расширяется от давления р ₀ до р ₁. При этом потенциальное давление рабочего тела преобразуется в кинетическую энергию. Далее в рабочей решётке происходит дальнейшее понижение давления от р ₁ до р ₂. Одновременно поток рабочего тела в рабочей решётке меняет направление. При этом происходит передача кинетической энергии потока рабочим лопаткам ступени.

Рис. 26

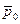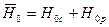Если бы течение рабочего тела в рабочей решётке происходило без потерь, то расширение от давления р ₀ до р ₁ привело бы к дальнейшему уменьшению энтальпии на (рис. 26), так что располагаемый теплоперепад для всей ступени, подсчитываемый от параметров торможения , , составил бы сумму располагаемых теплоперепадов сопловой и рабочей решёток, или, что почти то же самое, располагаемый теплоперепад ступени может быть взят по изоэнтропе между давлениями 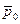и р ₂.

В действительном процессе из-за потерь расширение в рабочем канале происходит при возрастающей энтропии, так что состояние рабочего тела при выходе из рабочей решётки может быть представлено точкой 2 в h, s – диаграмме на рис. 26.

Отношение теплового перепада H _0p к теплоперепаду ступени от параметров торможения называется степенью реактивности:

. (59)

Если степень реактивности ступени равна нулю и в каналах рабочих лопаток не происходит дополнительного расширения рабочего тела, то такая ступень называется чисто активной. Также ступень называется активной, если ρ<0.25. Если степень реактивности значительно больше 0.25 (ρ = 0.4 – 0.6), то ступень называется реактивной.

Установленные на диске рабочего колеса лопатки образуют рабочую решётку и вращаются вместе с диском с угловой скоростью ω и соответственно с окружной скоростью u= 0.5 ωd, где d – диаметр ступени.

Выходящий из сопловой решётки со скоростью с ₁ поток направляется в рабочую решётку, по отношению к которой обладает относительной скоростью w ₁. Последняя определяется как разность векторов с ₁ и u (рис. 25) и составляет угол β ₁ с направлением окружной скорости u.

Направление относительной скорости w ₂рабочего тела при выходе из лопаточного канала определяется углом выхода из рабочей решётки β ₂.

Абсолютная скорость выхода рабочего тела из каналов рабочих лопаток определяется как сумма векторов относительной скорости w ₂ и окружной скорости u ₂ и обозначается с ₂.

Поворот и ускорение струи рабочего тела в криволинейных каналах рабочей решётки происходят под влиянием следующих усилий:

· струя испытывает реактивное усилие стенок канала;

· рабочее тело, заполняющий канал, испытывает разность давлений р ₁ - р ₂ при входе в канал и выходе из него.

Равнодействующая этих усилий, с которыми лопатки действуют на струю рабочего тела, обозначается R’. С другой стороны струя рабочего тела развивает на лопатках усилие R, равное, но прямо противоположное усилию R’ (рис.24).

Обычно усилие R раскладывают на две составляющие:

· усилие в направлении окружной скорости R _u - окружное усилие;

· усилие в направлении оси вращения диска ступени R _а – осевое усилие.

Окружное усилие может быть найдено на основании уравнения количества движения, записанного для оси u при массовом расходе рабочего тела, равном G, кг/с:

. (60)

Осевое усилие R _а может быть найдено из уравнения количества движения в направлении оси а, учитывая при этом разность давлений р ₁ - р ₂ , действующих на кольцевую площадь рабочих лопаток Ω=π d ₂ l ₂:

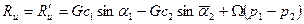. (61)

В выражениях (60) и (61) α₁ и - углы направления скоростей с ₁ и с ₂ (рис. 25).

В практики расчётов турбин принято при построении треугольников скоростей потока рабочего тела совмещать вершины треугольников скоростей входа и выхода рабочего тела, как показано на рис. 27.

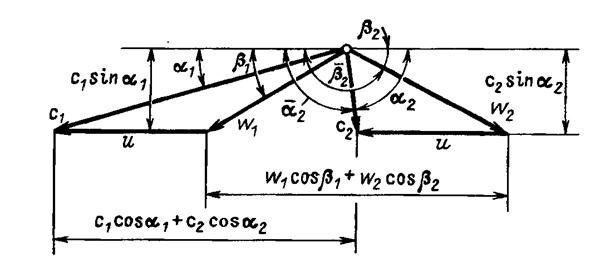
Рис. 27

Кроме того, углы β₂ и α₂ между направлениями относительной и абсолютной скоростей выхода рабочего тела w ₂ и с ₂ и направлением окружной скорости u обычно отсчитывают по часовой стрелки, так что между углами и , входящими в уравнения (60) и (61) и углами β ₂ и α ₂, применяемыми в практике расчётов турбин, существует связь:

= π - β ₂ и = π - .

В этом случае формула (60) примет вид:

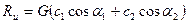. (62)

Обычно в осевых турбинах принято равенство u ₁ = u ₂ = const. Тогда

. (63)

Осевая составляющая усилия рабочего тела на лопатки запишется следующим образом:

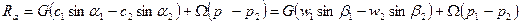. (64)

Входящие в (63) и (64) суммы проекций относительных и абсолютных скоростей рабочего тела могут быть непосредственно взяты из треугольников скоростей. Применяя формулы косоугольных треугольников, получаем:

;

.

Окружная мощность ступени может быть найдена из уравнения:

. (65)

Для расхода рабочего тела в 1кг/с запишем

. (66)

Преобразуем уравнение (66):

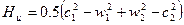. (67)

Абсолютную скорость с ₁ можно найти из уравнения (12): учитывая, что

. (68)

Потерю энергии в сопловой решётке можно определить из уравнения:

, [Дж/кг] (69)

где φ = с ₁/ с _1t.

Относительную скорость рабочего тела при входе в рабочую решётку w ₁ можно определить из треугольника скоростей (рис. 27).

Можно записать уравнение сохранения энергии при расширении рабочего тела от давления р ₁ до давления р ₂ в рабочей решётке при отсутствии теплообмена:

.

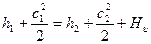Используя соотношение (67), найдём:

,

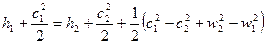или

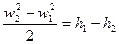. (70)

Из уравнения (70) находим относительную скорость на выходе из рабочей решётки:

. (71)

При расширении рабочего тела по изоэнтропе теоретическую относительную скорость можно определить из соотношения:

. (72)

Потерю энергии в рабочей решётке можно определить из выражения:

, (71)

где - коэффициент скорости рабочей решётки.

Потери энергии с выходной скоростью рабочего тела можно определить из выражения:

. (73)

Так как рабочее тело покидает ступень со скоростью c ₂, то его кинетическая энергия не используется в данной ступени.

Тогда

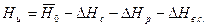. (74)

На рис. 28 детально изображён весь тепловой процесс в турбинной ступени в h, s -диаграмме (а) и показано определение удельного объёма рабочего тела v_2t по основной изоэнтропе (б).

Рис. 28

Мощность ступени N_u, кВт, - мощность на лопатках турбинной ступени (окружную мощность) можно определить по формуле:

N_u = GH_u, (75)

где G – расход рабочего тела в кг/с,

H_u – в кДж/кг.

Дата добавления: 2014-01-04