Основные уравнения и методы расчёта

Расчёт ступени с учётом изменения параметров потока по радиусу

Лекция № 10

Выше изложенные расчёты относились к среднему диаметру ступени и они могут быть справедливы по всей высоте лопаток только в тех случаях. Когда d/l > 10 – 15. При меньших значениях (d/l < 10) в кольцевых решётках линии тока проходят по сложной пространственной траектории. На рис. 33 изображена турбинная ступень с меридиональными линиями тока.

Рис. 33

Вектор скорости с в данной пространственной задаче разлагается на три составляющие:

, (107)

(рис. 34) связанные между собой на цилиндрической поверхности α и в меридиональной плоскости ν. На рис. 34 показан параллелепипед абсолютных скоростей в цилиндрической системе координат.

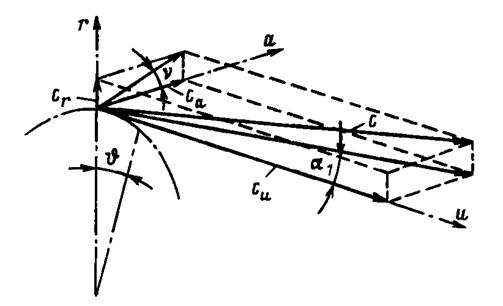
Рис. 34

Тогда составляющие скорости с можно записать в виде:

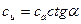; (108)

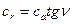; (109)

. (110)

Задачу пространственного потока рабочего тела в ступенях большой верности можно решить, произведя расчёт при переменных по радиусу параметрах потока.

Используя цилиндрическую систему координат (рис. 34), запишем для установившемся движении:

Уравнения количества движения (уравнения Эйлера)

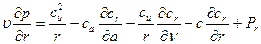; (111)

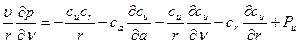; (112)

(113)

и уравнение неразрывности:

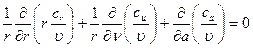, (114)

где Р_а, Р_u и Р_r - составляющие внешних сил.

В настоящее время расчёты пространственного потока в целом проводятся, как правило, упрощённо – для осесимметричного потока, т.е. в предположении 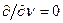. При этом упрощённые уравнения количества движения не учитывают массовых сил воздействия лопаток на поток Р, что справедливо для пространства вне решёток, в частности для сечений 0 – 0, 1 – 1, 2 – 2 (рис. 34). Для сопловой решётки используем уравнения (111), (112) и (113). К ним добавляем уравнение изоэнтропы:

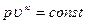(115)

И уравнение сохранения энергии, записанной для линии тока,

. (116)

Для решения системы из пяти уравнений, записанных для кольцевой сопловой решётки, с пятью неизвестными р, υ, с_u, c_a и с_r должны быть заданы дополнительные параметры и характеристики решёток. Обычно задают расход рабочего тела и угловую скорость ω.

Кроме перечисленных условий решение задачи требует ещё замыкающего соотношения, называемого законом закрутки, который будет рассмотрен ниже.

Решив совместно эти уравнения окончательно получим уравнение, определяющее изменение скоростей потока 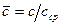по радиусу:

.(117)

На основании уравнения (117) проанализируем влияние ряда параметров на распределение давления р ₁ и скорости с _1t в зазоре между решётками.

Рассмотрим некоторые частные случаи.

1. В частном случае цилиндрических поверхностей тока (рис. 35, а), т.е. при tg v = 0, получаем простое уравнение:

. (118)

Его решение записывается в виде:

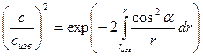, (119)

где индекс «изв» относится к радиусу r _изв, на котором из предварительного расчёта известны параметры потока, в том числе скорость с _изв.

Как видно из (119), от корня к периферии скорость потока уменьшается, причём тем больше, чем меньше угол α, т.е. чем больше закрутка потока.

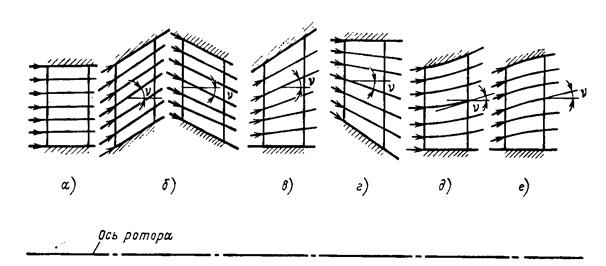
Рис. 35

2. В частном случае ступени с коническими поверхностями тока tg v =const (рис.35, б) скорость потока от корня к периферии уменьшается сильнее, чем в цилиндрической схеме (случай 1). Влияние конусности потока оказывается тем большим, чем больше число М_а.

3. В решётке с коническими поверхностями тока и увеличением абсолютного угла наклона их от корня к периферии (рис. 35, в) скорость падает в ещё большей степени (например, ступень с корневым цилиндрическим и периферийным коническим обводами, рис. 33).

Обратная картина будет наблюдаться для решётки, изображённой на рис. 35, г.

4. В случае кривизны меридиональных линий тока на участке с выпуклостью их к оси решётки (рис. 35, д) уменьшение скорости к периферии замедляется (рис. 36), и, наоборот, увеличивается разница в скоростях при вогнутой к оси форве меридиональной линии тока (рис. 35, е).

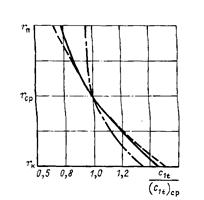
Рис 36

На рис. 36 показано распределение скорости потока с θ = 2.75 при (M _1t)_к = 1, где — - расчёт в предположении ν = 0; ----- расчёт в предположении dv\da =0;

— ∙ — ∙ — - расчёт по (117) и меридиональным линиям тока согласно рис. 35, д.

Как видим, форма и наклон линий тока зависят от многих параметров.

В первом приближении для ступеней с цилиндрическими меридиональными обводами может служить гипотеза о цилиндрических поверхностях тока. Тогда, если для элементарной массы потока в зазоре между решётками найти центробежную силу, то из условия радиального равновесия этой массы получим:

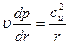. (120)

Полагая, что как перед, так и за ступенью 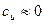, то из формулы (120) следует постоянство давлений р₀, р₁ и р₂ по радиусу в сечениях между решётками. Тогда при постоянстве температуры по радиусу перед сопловой решёткой располагаемый теплоперепад ступени не будет меняться по радиусу, и согласно уравнению (68) можно получить формулу для определения изменения по радиусу степени реактивности:

. (121)

Таким образом, для того, чтобы по упрощённому уравнению радиального равновесия определить изменения по радиусу степени реактивности, необходимо знать зависимост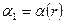и и .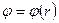

Зависимость 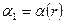является упомянутым выше соотношением, называемым законом закрутки сопловой решётки.

Дата добавления: 2014-01-04