Построение математической модели

Цель задачи состоит в минимизации суммарной стоимости на перевозки. Эта цель может быть достигнута с помощью оптимальной организации перевозок сырья. Следовательно, за неизвестные можно принять количество сырья, перевозимого от каждого поставщика каждому потребителю.

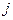Пусть – количество сырья, перевозимого от -го поставщика -му потребителю. Параметры задачи – число поставщиков и потребителей, предложение и спрос сырья в каждом пункте, тарифы на перевозки.

Ограничения задачи – это ограничения на предложение и спрос сырья. Предложения сырья всех поставщиков не должны быть меньше суммарного спроса на него во всех пунктах потребления. В данной задаче имеет место точное равенство между предложением и спросом.

120+50+190+110=160+140+170=470.

Количество сырья, вывозимого от каждого поставщика, должно быть равно наличному количеству сырья. Количество сырья, доставленное каждому потребителю, должно равняться его спросу. Последнее ограничение – условие неотрицательности .

Критерием эффективности (целевой функцией) являются суммарные затраты 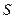на перевозку, равные сумме произведений тарифов на перевозку, на количество перевозимого сырья от каждого поставщика каждому потребителю.

Окончательно математическая модель задачи имеет вид

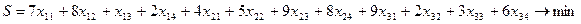
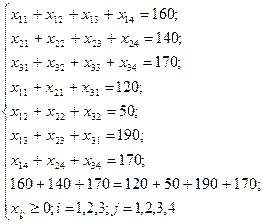
Целевая функция и ограничения линейны, т.е. данная задача относится к задачам линейного программирования, однако, благодаря особой структуре, эта задача получила специальное название: транспортная задача или транспортная модель.

Дата добавления: 2014-01-04