Определение 3.2.3

Определение 3.2.2

Задача (3.2.1)–(3.2.5) называется несбалансированной транспортной моделью (задачей).

Задача (3.2.1)-т-(3.2.5), в которой ограничения (3.2.2)–(3.2.4) имеют вид равенств, называется сбалансированной транспортной моделью (задачей).

Покажем, что любую несбалансированную транспортную модель можно свести к сбалансированной.

Пусть суммарное предложение больше суммарного спроса, т.е.

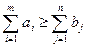(3.2.6)

Введем фиктивного (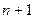) -го потребителя, спрос которого

,

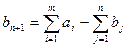а тариф на перевозку этому потребителю от всех поставщиков равен 0.

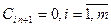
Очевидно, при этом неравенства (3.2.2) и (3.2.3) перейдут в равенство, и к ним добавится ограничение (равенство) для ( 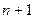)-го пункта потребления.

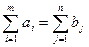
Естественно, что в реальных задачах суммарное предложение может быть меньше суммарного спроса, т.е.

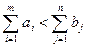(3.2.7)

Транспортные задачи, содержащие ограничение (3.2.7), также являются несбалансированными и могут быть сведены к сбалансированным с помощью ввода фиктивного (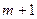)-го поставщика, предложение которого

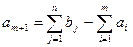
стоимость перевозки от (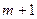)-го поставщика нулевая,

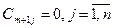
Неравенство (3.2.7) перейдет в равенство

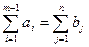
Рассмотрим сбалансированную транспортную задачу

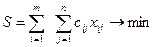(3.2.8)

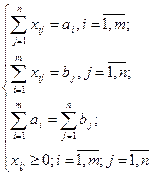(3.2.9)(3.2.10)(3.2.11)(3.2.12)

Как отмечалось выше, для решения задачи может быть применен симплекс-метод, но ее особая структура (все ограничения имеют вид равенств, в которые неизвестные входят с коэффициентами, равными 1) позволяет решать ее более простыми методами.

Для решения транспортной задачи составляют транспортную таблицу (табл. 3.2.1).

Таблица 3.2.1

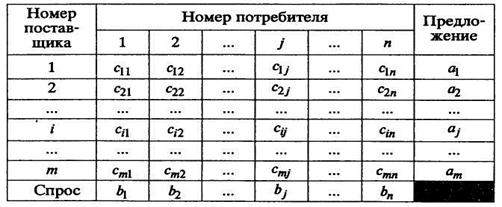
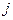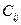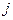В левой колонке и верхней строке таблицы записаны соответственно номера поставщиков и потребителей. В правой колонке и нижней строке записаны, соответственно, предложения каждого поставщика и спрос каждого потребителя. В правом верхнем углу клетки, стоящей на пересечении -й строки и -го столбца, стоит тариф на перевозку от -го поставщика -му потребителю (, ).

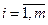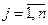Решение транспортной задачи записывают в клетки транспортной таблицы: на пересечении -й строки и 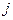-го столбца записывается значение .

Решение транспортной задачи, как и решение ОЗЛП, состоит из двух этапов:

1 этап. Нахождение начального плана перевозок (), 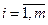; 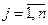, удовлетворяющего ограничениям (3.2.9) – (3.2.12);

2 этап. Улучшение начального плана перевозок и получение оптимального плана перевозок (),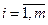; 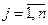, доставляющего минимум функции (3.2.8).

Заметим, что общее число неизвестных в транспортной задаче равно 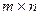. Уравнения (3.2.9), (3.2.10) не являются линейно-независимыми, так как их правые части связаны условием (3.2.11). Чис­ло линейно-независимых уравнений в ограничениях транспортной задачи равно, следовательно, не 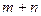, а . Таким образом, число неизвестных больше числа связывающих их уравнений так же, как и в основной задаче линейного программирования.

Систему уравнений (3.2.9), (3.2.10) можно разрешить относительно базисных переменных. Остальные 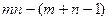переменных являются свободными. Каждое решение транспортной задачи находят следующим образом: свободные 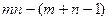переменные полагаются равными нулю, а базисные переменные находят из системы ограничений (3.2.9) – (3.2.10). Полученное решение проверяют на оптимальность. Если решение неоптимально, то осуществляют переход к новому решению путем изменения списка базисных переменных. Эти действия повторяют до тех пор, пока не будет получено оптимальное решение, доставляющее ми­нимум целевой функции (3.2.8).

3.3. Определение начального плана транспортировок. Методы "северо-западного" угла, минимального элемента, Фогеля

Рассмотрим три метода нахождения начального решения транспортной задачи: метод "северо-западного" угла, метод минимального элемента и метод Фогеля.

Метод "северо-западного" угла

Шаг 1. Составляют транспортную таблицу.

Шаг 2. Транспортную таблицу начинают заполнять с левого верхнего (северо-западного) угла. При заполнении двигаются по строке вправо и по столбцу вниз. В клетку, находящуюся на пересечении первой строки и первого столбца, помещается максимально возможное число единиц продукции, разрешенное ограничениями на предложение и спрос: 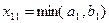. Если 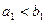, то 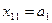и предложение первого поставщика полностью исчерпано. Первая строка вычеркивается, и двигаются по столбцу вниз. В клетку, находящуюся на пересечении первого столбца и второй строки, помещается максимально возможное число единиц продукции, разрешенное ограничениями на предложение и спрос: 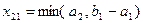. Если 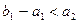, то 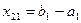. Спрос первого потребителя удовлетворен. Первый столбец вычеркивают и двигаются по второй строке вправо. Заполнив клетку, стоящую на пересечении второй строки и второго столбца, переходят к заполнению следующей третьей клетки второй строки, либо второго столбца. Процесс продолжают до тех пор, пока не исчерпается предложение и не удовлетворится спрос. Последняя заполненная клетка находится в последнем 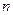-м столбце и последней -й строке.

Дата добавления: 2014-01-04