Пример 3.3.3

Метод Фогеля

Шаг 1. Составляют транспортную таблицу.

Шаг 2. Для каждой строки и каждого столбца транспортной таблицы определяют разность между наименьшим тарифом и ближайшим к нему значением. Переход к шагу 3.

ШаеЗ. В строке или в столбце, которым соответствует наибольшая разность, выбирают клетку с наименьшим тарифом. Переход к шагу 4.

Шаг 4. В выбранную клетку, аналогично предыдущим методам, записывают максимально возможное число единиц продукции, которое разрешается ограничениями на предложение и спрос. После этого вычеркивают либо строку, если предложение поставщика исчерпано, либо столбец, если спрос потребителя удовлетворен.

Если все клетки таблицы заполнены или вычеркнуты, то план перевозок построен. В противном случае переходят к шагу 2 без учета вычеркнутых и заполненных клеток.

В методе Фогеля используются штрафы, взимаемые за неудачный выбор маршрута. Рассчитанные на шаге 2 разности между двумя уровнями затрат на перевозку являются штрафами за неверно выбранный маршрут перевозки.

Определим начальное решение по методу Фогеля для транспортной задачи из примера 3.1.1 (табл. 3.3.3).

Решение.

Таблица 3.3.3

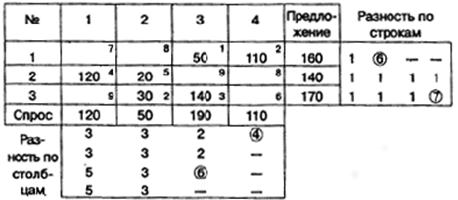
Разности по строкам будем записывать в правой части табл. 3.3.3, разности по столбцам – внизу табл. 3.3.3. Максимальную разность будем отмечать кружком. Наименьший тариф в первой строке равен 1. Ближайший к нему равен 2. Разность равна 1. Наименьший тариф во второй строке 4. Ближайшее к нему значение 5. В третьей строке 2 и 3, соответственно. Разности по всем строкам равны 1.

В первом столбце наименьший тариф . Ближайшее значение 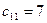, 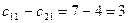. Во втором столбце наименьшее значение . Ближайшее значение , .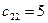

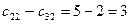Третий столбец: , , .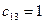

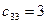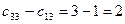Четвертый столбец: , , .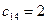

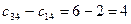Максимальная из всех разностей 4 находится в четвертом столбце. В этом столбце клетка с наименьшим тарифом 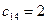находится в первой строке. В эту клетку помещаем максимально возможное значе­ние: 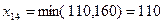. Четвертый потребитель полностью удов­летворил свой спрос, и четвертый столбец вычеркиваем.

Повторяем предыдущие действия без учета вычеркнутых и запол­ненных клеток.

Первая строка: минимальный тариф 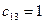. Ближайшее значение , .

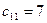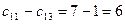Вторая строка: минимальный тариф . Ближайшее значение , .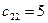

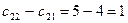Третья строка: , , .

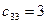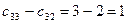Первый столбец: минимальный тариф . Ближайшее значе­ние , .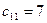

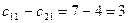Второй столбец: , , .

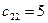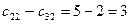Третий столбец: , , .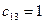

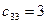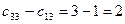Максимальная разность равна 6 и стоит в первой строке. Минимальный тариф в первой строке 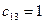. В эту клетку помещаем 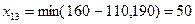. Вычеркиваем первую строку.

Повторяем все действия без учета первой строки и четвертого столбца.

Вторая строка: , , .

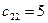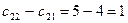Третья строка: , , .

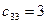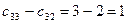Первый столбец: , , .

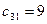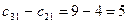Второй столбец: , , .

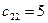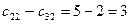Третий столбец: , , .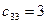

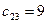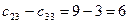Максимальная разность равна 6 и стоит в третьем столбце. Мини­мальный из оставшихся тарифов в этом столбце 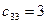, 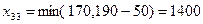. Спрос третьего потребителя удовлетво­рен, третий столбец вычеркиваем.

Вновь составляем разности для невычеркнутых строк и столбцов.

Вторая строка: , , .

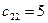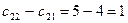Третья строка: , , .

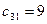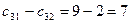Первый столбец: , , .

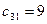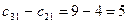Второй столбец: , , .

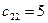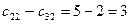Максимальная разность стоит в третьей строке. Минимальный та­риф в этой строке , .

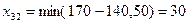Предложение поставщика исчерпано, и третью строку вычеркиваем.

Осталась одна строка транспортной таблицы. Это вторая строка. В этой строке сначала заполняем клетку с наименьшим тарифом , . Оставшееся предложение вто­рого поставщика записываем в единственную свободную клетку .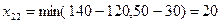

Полученный по методу Фогеля план перевозок имеет вид

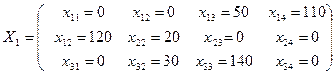
Затраты на перевозку по этому плану составляют

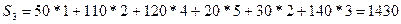
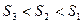
Таким образом, для одной и той же транспортной задачи полу­чены различные начальные планы перевозок, построенные с ис­пользованием разных методов. При этом затраты на перевозки составляют соответственно: 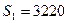, , 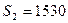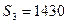. Метод Фогеля наиболее трудоемкий, однако начальный план перевозок, построенный с его использованием, обычно бывает близок к оп­тимальному плану, а в некоторых случаях является оптимальным планом.

Изложенные методы нахождения начального решения не един­ственные. В качестве начального решения может быть взят любой набор чисел, удовлетворяющих ограничениям (3.2.9)—(3.2.12) (на­пример, полученный по методу "юго-восточного" угла). Читатель может придумать свой собственный метод получения начального решения.

Дата добавления: 2014-01-04