Оптимальное распределение оборудования

Экономические задачи, сводящиеся к транспортным моделям

В этом параграфе будет рассмотрено несколько примеров экономических задач, оптимальное решение которых может быть найдено с помощью транспортных моделей.

Оборудование -различных видов нужно распределить между 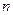-рабочими участками. Производительность одной единицы оборудования -го вида на 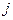-м рабочем участке равна 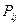; ; 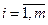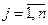. Потребность 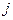-го участка в оборудовании составляет 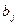, 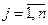. Запас оборудования -ro вида равен , 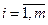. Найти распределение оборудования на рабочие участки, при котором суммарная производительность максимальная.

Решение.

Данная задача относится к классу транспортных задач при условии, что производительность линейно зависит от количества используемого оборудования. Поставщиками в задаче являются различные виды оборудования, потребителями – рабочие участки. Предложение определяется запасом оборудования каждого вида, спрос – потребностью в нем на рабочем участке.

Обозначим через число единиц оборудования -го вида, выделенное на 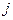-й рабочий участок, 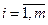; 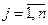. Математическая модель задачи имеет следующий вид:

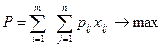
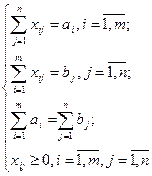
Построенная модель является сбалансированной. Если запас оборудования и потребность в нем не равны, то переход к сба­лансированной модели осуществляется с помощью преобразова­ний, изложенных в параграфе 3.2.

В данной задаче требуется максимизировать целевую функцию 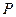, представляющую суммарную производительность. Для перехода к стандартной транспортной модели надо заменить функцию 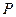на противоположную функцию 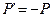, которую нужно будет минимизировать.

При решении в транспортной таблице вместо тарифов на перевозки запишутся производительности 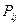, взятые с противоположным знаком. Далее задача решается известными методами, представленными в этой главе.

Дата добавления: 2014-01-04