Пример 4.4.1

Расчет экономико-математической модели при нелинейных затратах на производство

Рассмотрим применение изученных методов на примере решения задачи оптимальной реализации продукции.

Фирма реализует автомобили двумя способами: через магазин и через торговых агентов. При реализации автомобилей через магазин расходы на реализацию составляют усл. ед., а при продаже автомобилей через торговых агентов расходы составляют усл. ед. Найти оптимальный способ реализации автомобилей, минимизирующий суммарные расходы, если общее число предназначенных для продажи автомобилей составляет 200 штук.

Решение.

Составим математическую модель задачи.

Целью является минимизация суммарных расходов

.

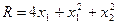Управляющие переменные – это число автомобилей, реализуемых первым и вторым способом: и соответственно (200 штук). Окончательно математическая модель имеет следующий вид:

.

.

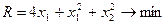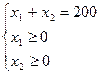Для ее расчета применим метод множителей Лагранжа. Функция Лагранжа имеет вид

.

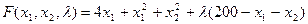Найдем частные производные функции 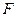по , и 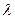и приравняем их к нулю.

Получим следующую систему уравнений:

.

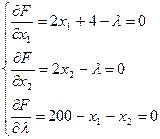Решая систему, найдем

=99, =101, 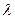=202, 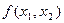=20398.

Определитель, составленный из вторых частных производных функций 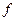по , , имеет вид

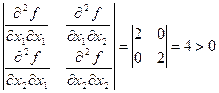
Следовательно, по теореме о достаточном условии существования условного экстремума функция 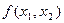в точке =99, = 101 действительно имеет экстремум.

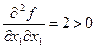
следовательно в этой точке функция 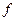имеет условный минимум.

Таким образом, для получения минимальных расходов, нужно реализовать 99 автомобилей через магазин и 101 автомобиль через торговых агентов. При этом расходы на реализацию составят 20398 усл. ед.

Данную задачу можно было решить и графическим методом (рис. 4.4.1).

Рис. 4.4.1

Областью допустимых решений задачи является отрезок АВ, линиями уровня функции 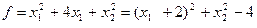являются концентрические окружности 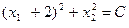с центром в точке =-2, =0 и радиусом .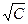

Из рисунка видно, что минимальное значение функции, принадлежащее области допустимых решений, достигается в точке 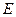, в которой совпадают угловой коэффициент прямой =200-и касательной к окружност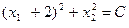и к оси .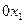

Продифференцировав последнее уравнение по , получим

,

.

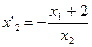Приравняем последнее выражение к угловому коэффициенту прямой и добавим к этому уравнению уравнение прямой, которой принадлежит точка Е.

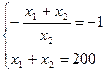
Решив последнюю систему, найдем оптимальные значения: =99, =101, 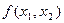=20398.

Дата добавления: 2014-01-04