Составление математической модели динамического программирования

Дополнительно введем следующие условные обозначения:

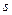– состояние процесса;

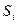– множество возможных состояний процесса перед -м шагом;

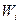– выигрыш с -го шага до конца процесса, .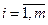

Можно определить следующие основные этапы составления математической модели задачи динамического программирования.

1. Разбиение задачи на шаги (этапы). Шаг не должен быть слишком мелким, чтобы не проводить лишних расчетов и не должен быть слишком большим, усложняющим процесс шаговой оптимизации.

2. Выбор переменных, характеризующих состояние 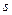моделируемого процесса перед каждым шагом, и выявление налагаемых на них ограничений. В качестве таких переменных следует брать факторы, представляющие интерес для исследователя, например годовую прибыль при планировании деятельности предприятия.

3. Определение множества шаговых управлений 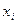, 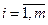и налагаемых на них ограничений, т.е. области допустимых управлений X.

4. Определение выигрыша

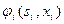(5.2.1)

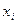который принесет на -м шаге управление , если система пе­ред этим находилась в состоянии s.

5. Определение состояния 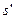, в которое переходит система из состояния s под влиянием управления ,

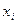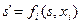(5.2.2)

где 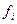– функция перехода на -м шаге из состояния s в состояние .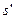

6. Составление уравнения, определяющего условный оптимальный выигрыш на последнем шаге, для состояния s моделируе­мого процесса

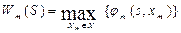(5.2.3)

7. Составление основного функционального уравнения динамического программирования, определяющего условный оптимальный выигрыш для данного состояния s с -гo шага и до конца процесса через уже известный условный оптимальный выигрыш с (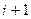)-го шага до конца:

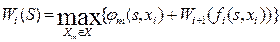(5.2.4)

В уравнении (5.2.4) в уже известную функцию , характеризующую условный оптимальный выигрыш с (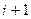)-го шага до конца процесса, вместо состояния s подставлено новое состояние 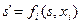в которое система переходит на -м шаге под влиянием управления .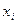

Заметим, что структура модели динамического программирования отличается от статической модели линейного программирования. Действительно, в моделях линейного программирования управляющие переменные – это одновременно и переменные состояния моделируемого процесса, а в динамических моделях отдельно вводятся переменные управления 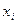, и переменные, характеризующие изменение состояния s под влиянием управления. Таким образом, структура динамических моделей более сложная, что естественно, так как в этих моделях дополнительно учитывается фактор времени.

Дата добавления: 2014-01-04