
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Основы теории напряженного состояния
|
|
|
|
Напряженное состояние в точке – совокупность напряжений, действующих во множестве площадок, проходящих через данную точку.
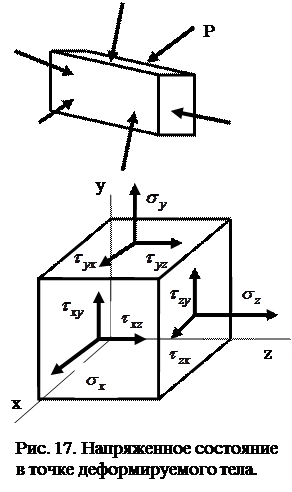
Исследуя напряженное состояние в данной точке деформируемого тела, в ее окрестностях выделяют бесконечно малый (элементарный) параллелепипед, ребра которого направлены вдоль соответствующих координатных осей.
При действии на тело внешних сил на каждой из граней элементарного параллелепипеда возникают напряжения, которые представляют нормальными и касательными напряжениями – проекциями полных напряжений на координатные оси.
Таким образом, на гранях элементарного параллелепипеда, выделенного в окрестности точки нагруженного тела, действует девять компонентов напряжения. Запишем их в виде матрицы, которая называется тензором напряжений
 (3.10)
(3.10)
Не все девять компонентов напряжений, действующих на гранях параллелепипеда, независимые (несвязанные друг с другом). В этом легко убедиться, составив уравнения равновесия суммы моментов относительно координатных осей. Записав уравнения моментов от сил, действующих по граням параллелепипеда, и пренебрегая их изменением при переходе от одной грани к другой ей параллельной, получим, что
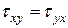 ,
,  ,
, 
 Данные равенства называют законом парности касательных напряжений.
Данные равенства называют законом парности касательных напряжений.
Закон парности касательных напряжений: на взаимно перпендикулярных площадках действуют равные по величине и противоположно направленные касательные напряжения.
В окрестности исследуемой точки можно выделить бесконечное множество взаимно перпендикулярных площадок. В том числе можно найти такие площадки, по граням которых действуют только нормальные напряжения, а касательные напряжения равны нулю. Такие площадки называют главными.
Главные площадки – три взаимно перпендикулярные площадки в окрестности исследуемой точки, на которых касательные напряжения равны нулю.
Главные напряжения – нормальные напряжения, действующие по главным площадкам.
На главных площадках нормальные напряжения принимают свои экстремальные значения 
Тензор напряжений для главных площадок: 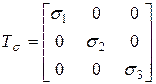 (3.11)
(3.11)
В зависимости от того, сколько главных напряжений действует в окрестности данной точки, различают три вида напряженного состояния:
1. Линейное (одноосное) – если одно главное напряжение отлично от нуля, а два других равны нулю ( ,
,  ,
,  );
);
2. Плоское (двухосное) – если два главных напряжения отличны от нуля, а одно равно нулю ( ,
, 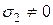 ,
,  );
);
3. Объемное (трехосное) – если все три главных напряжения отличны от нуля ( ,
, 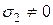 ,
, 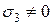 );
);
 Напряженное состояние в точке при плоском напряженном состоянии можно описать с помощью круга Мора, построенного в координатных осях
Напряженное состояние в точке при плоском напряженном состоянии можно описать с помощью круга Мора, построенного в координатных осях  и
и 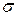 . Здесь
. Здесь  и
и 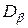 точки, соответствующие напряженному состоянию на любых двух взаимно перпендикулярных площадках
точки, соответствующие напряженному состоянию на любых двух взаимно перпендикулярных площадках  и
и  с координатами (
с координатами ( ;
;  ) и (
) и ( ;
; 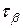 ) соответствен-но. Через эти две точки проводится окружность радиусом
) соответствен-но. Через эти две точки проводится окружность радиусом  или
или  (точка С – центр круга Мора). В точках, где круг Мора пересекает ось
(точка С – центр круга Мора). В точках, где круг Мора пересекает ось 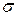 можно найти величину главных нормальных напряжений
можно найти величину главных нормальных напряжений 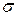 (так как касательные напряжения равны нулю.
(так как касательные напряжения равны нулю.
|
|
|
|
Дата добавления: 2014-01-04; Просмотров: 473; Нарушение авторских прав?; Мы поможем в написании вашей работы!