Постоянный электрический ток. Закон Ома

Потенциал

Электростатическое поле обладает важным свойством:

Работа сил электростатического поля при перемещении заряда из одной точки поля в другую не зависит от формы траектории, а определяется только положением начальной и конечной точек и величиной заряда.

Аналогичным свойством обладает и гравитационное поле, и в этом нет ничего удивительного, так как гравитационные и кулоновские силы описываются одинаковыми соотношениями.

Следствием независимости работы от формы траектории является следующее утверждение:

Работа сил электростатического поля при перемещении заряда по любой замкнутой траектории равна нулю.

Силовые поля, обладающие этим свойством, называют потенциальными или консервативными.

Свойство потенциальности электростатического поля позволяет ввести понятие потенциальной энергии заряда в электрическом поле. Для этого в пространстве выбирается некоторая точка (0), и потенциальная энергия заряда q, помещенного в эту точку, принимается равной нулю.

Потенциальная энергия заряда q, помещенного в любую точку (1) пространства, относительно фиксированной точки (0) равна работе A10, которую совершит электростатическое поле при перемещении заряда q из точки (1) в точку (0): Wp1 = A10

Физическую величину, равную отношению потенциальной энергии электрического заряда в электростатическом поле к величине этого заряда, называют потенциалом φ электрического поля:

Если изолированный проводник поместить в электрическое поле то на свободные заряды q в проводнике будет действовать сила . В результате в проводнике возникает кратковременное перемещение свободных зарядов. Этот процесс закончится тогда, когда собственное электрическое поле зарядов, возникших на поверхности проводника, скомпенсирует полностью внешнее поле. Результирующее электростатическое поле внутри проводника будет равно нулю.

Однако, в проводниках при определенных условиях может возникнуть непрерывное упорядоченное движение свободных носителей электрического заряда. Такое движение называется электрическим током. За направление электрического тока принято направление движения положительных свободных зарядов. Для существования электрического тока в проводнике необходимо создать в нем электрическое поле.

Количественной мерой электрического тока служит сила тока I – скалярная физическая величина, равная отношению заряда Δq, переносимого через поперечное сечение проводника за интервал времени Δt, к этому интервалу времени:

Если сила тока и его направление не изменяются со временем, то такой ток называется постоянным.

Немецкий физик Г. Ом в 1826 году экспериментально установил, что сила тока I, текущего по однородному металлическому проводнику (т. е. проводнику, в котором не действуют сторонние силы), пропорциональна напряжению U на концах проводника:

Величину R принято называть электрическим сопротивлением. Проводник, обладающий электрическим сопротивлением, называется резистором. Данное соотношение выражает закон Ома для однородного участка цепи: сила тока в проводнике прямо пропорциональна приложенному напряжению и обратно пропорциональна сопротивлению проводника.

В СИ единицей электрического сопротивления проводников служит ом (Ом). Сопротивлением в 1 Ом обладает такой участок цепи, в котором при напряжении 1 В возникает ток силой 1 А.

Для участка цепи, содержащего ЭДС, закон Ома записывается в следующей форме: IR = U12 = φ1 – φ2 + 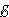= Δφ12 +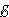

Это соотношение принято называть обобщенным законом Ома или законом Ома для неоднородного участка цепи.

Эта формула выражет закон Ома для полной цепи: сила тока в полной цепи равна электродвижущей силе источника, деленной на сумму сопротивлений однородного и неоднородного участков цепи.

17.Энергия электрического поля. Закон Джоуля – Ленца

Опыт показывает, что заряженный конденсатор содержит запас энергии.

Энергия заряженного конденсатора равна работе внешних сил, которую необходимо затратить, чтобы зарядить конденсатор.

Процесс зарядки конденсатора можно представить как последовательный перенос достаточно малых порций заряда Δq > 0 с одной обкладки на другую (рис. 1.7.1). При этом одна обкладка постепенно заряжается положительным зарядом, а другая – отрицательным. Поскольку каждая порция переносится в условиях, когда на обкладках уже имеется некоторый заряд q, а между ними существует некоторая разность потенциалов при переносе каждой порции Δq внешние силы должны совершить работу

Энергия Wе конденсатора емкости C, заряженного зарядом Q, может быть найдена путем интегрирования этого выражения в пределах от 0 до Q:

Рисунок 1.7.1. Процесс зарядки конденсатора

Формулу, выражающую энергию заряженного конденсатора, можно переписать в другой эквивалентной форме, если воспользоваться соотношением Q = CU.

Электрическую энергию Wе следует рассматривать как потенциальную энергию, запасенную в заряженном конденсаторе. Формулы для Wе аналогичны формулам для потенциальной энергии Eр деформированной пружины (см. ч. I, § 2.4)

где k – жесткость пружины, x – деформация, F = kx – внешняя сила.

По современным представлениям, электрическая энергия конденсатора локализована в пространстве между обкладками конденсатора, то есть в электрическом поле. Поэтому ее называют энергией электрического поля. Это легко проиллюстрировать на примере заряженного плоского конденсатора.

Напряженность однородного поля в плоском конденсаторе равна E = U/d, а его емкость.

Поэтому

где V = Sd – объем пространства между обкладками, занятый электрическим полем. Из этого соотношения следует, что физическая величина

является электрической (потенциальной) энергией единицы объема пространства, в котором создано электрическое поле. Ее называют объемной плотностью электрической энергии.

Энергия поля, созданного любым распределением электрических зарядов в пространстве, может быть найдена путем интегрирования объемной плотности wе по всему объему, в котором создано электрическое поле.

При протекании тока упорядоченное движение электронов поддерживается за счет энергии электрического поля. В результате соударений с ионами кристаллической решетки электроны передают свою энергию движения этим ионам и увеличивают скорость их хаотических тепловых колебаний. Таким образом, энергия движения электронов в результате столкновений с ионами приводит к нагреванию решетки, и протекание тока в проводнике должно сопровождаться выделением тепловой энергии. Джоуль и Ленц независимо друг от друга экспериментально установили, что количество тепла dQ, выделяющееся в проводнике пропорционально квадрату силы тока I, сопротивлению R проводника и времени dt:

dQ = I2Rdt(2.14)

Закон Джоуля-Ленца можно получить, представляя выделившееся в проводнике тепло как результат работы сил электрического поля по перемещению зарядов внутри проводника. Действительно, за промежуток времени dt по проводнику проходит заряд dq = Idt. Для перемещения этого заряда из одного конца проводника в другой электрическое поле совершает работу dA, которая выражается через разность потенциалов (напряжение) на концах проводника

dA = Udq = UIdt(2.15)

Пусть сопротивление рассматриваемого участка проводника равно R. Тогда, используя закон Ома из (2.15) получим:

dA = I2Rdt = (U2/R)dt(2.16)

Как указано выше эта работа dA пошла на нагревание проводника, то есть dA = dQ и мы в результате пришли к закону Джоуля-Ленца.

Работа тока, совершаемая в единицу времени представляет собой мощность тока. Из (2.15), (2.16) следует, что мощность тока Р равна

P = dA/dt = UI = I2R = U2/R(2.17)

Мощность тока также как и механическая мощность измеряется в ваттах (Вт). 1Вт = 1Дж/с.

Формула (2.14) выражает закон Джоуля-Ленца в интегральной форме, так как отображает тепло, выделившееся во всем объеме рассматриваемого проводника. Найдем теплоту, выделяющуюся малом элементарном объеме dV = dSdlпроводника. Согласно (2.12) сопротивление R этого объема равно r(dl/dS). Пусть j - плотность тока, протекающего через основание dS. По закону Джоуля-Ленца

dQ = I2Rdt = (jdS)2r(dl/dS)dt = rj2dVdt(2.18)

Количество теплоты, выделяющееся в единице объема в единицу времени называют удельной мощностью тока w.

w = dQ/dVdt

Из (2.18)

w = rj2(2.19)

Используя в (2.19) закон Ома в дифференциальной форме (), получим

w = (1/r)E2 = sE2(2.20)

Формулы (2.19), (2.20) выражают закон Джоуля-Ленца в дифференциальной форме.

Дата добавления: 2014-01-04