Рекурсия

End.

Begin

Begin

Repeat

Begin

Var

Var

End.

Begin

...

Begin

Var

Var

Функции

End.

Begin

Begin

Var

End.

Begin

...

Begin

Var

Type

Процедуры

<Объявление процедуры>:: =

procedure <Имя процедуры>[(<Список формальных параметров>)];

[<Разделы объявления локальных типов, констант, переменных>]

[<Разделы объявления локальных процедур и функций>]

begin	} ^Раздел исполнения процедуры
<Операторы>
end;

<Список формальных параметров> :: =

<Элемент списка 1>; <Элемент списка 2>; ...

<Элемент списка> :: =

<Список имён параметров-значений>: <Тип>

или

var <Список имён параметров-переменных>: <Тип>

или

const <Список имён параметров-констант>: <Тип>

<Обращение к процедуре> :: =

<Имя процедуры>[(<Список фактических параметров>)]

Замечание. Фактические параметры должны быть совместимы с формальными по типам.

Пример программы 2.

program Example2;

MyInt = integer;

I: MyInt;

J: integer;

procedure P2(var M: integer);

end;

P2(J); // Нормально

P2(I); // Ошибка

Пример программы 3.

program Example3;

I, J, K: integer;

procedure P3(L: integer; var M: integer; const N: integer);

Inc(L); // Бесполезно

Inc(M); // Полезно

(* Inc(N); *) // Ошибка

end;

I:= 1; J:= 1; K:= 1;

P3(I, J, K);

wri teln(‘I=’, I); // I = 1

wri teln(‘J=’, J); // J = 2

<Объявление функции>:: =

function <Имя функции>[(<Список формальных параметров>)]:

<Тип возвращаемого значения>;

<Разделы объявления локальных типов, констант, переменных>

<Разделы объявления локальных процедур и функций>

begin	} ^Раздел исполнения процедуры
<Операторы>
end;

Среди <Операторов> должен быть хотя бы один «Оператор» вида

<Имя функции>:= <Выражение>;

или

result:= <Выражение>;

Пример программы 4.

program Example4;

x, y, Eps: Double;

function BesselI0(x, Eps: Double): Double;

S, A, B, R: Double;

BesselI0:= S;

end;

writeln(‘x=? ’); readln(x);

writeln(‘Eps=? ’); readln(Eps);

y:= BesselI0(x, Eps); writeln(‘y=’, y);

x,y: Double;

function BesselI0(x, eps: Double): Double;

I, N: integer;

T, A, B, R, x2: Double;

x2:= sqr(x/2);

A:= x2;

N:= 0;

B:= x2 / (N + 2) / (N + 2);

inc(N);

A:= A * B;

B:= x2 / (N + 2) / (N + 2);

R:= A / (1 - B);

until (B < 1) and (R < eps);

T:= 1;

for I:= N downto 1 do

T:= 1 + x2 / I / I * T;

BesselI0:= T;

end;

x:= 3;

y:= BesselI0(x, 1e-20);

writeln(y);

readln;

end.

writeln(‘Введите x’); readln(x);

writeln(‘Введите eps’); readln(eps);

if (eps <= 0) or (eps >= 1) then exit;

writeln(‘f=’, BesselI(x, Eps));

readln;

Оконное приложение в среде Lazarus:

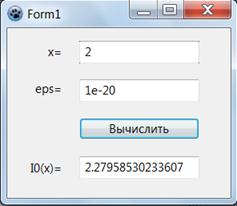
Текст кода в среде Lazarus:

unit Unit1;

{$mode objfpc}{$H+}

interface

uses

Classes, SysUtils, FileUtil, Forms, Controls, Graphics, Dialogs, StdCtrls;

type

{ TForm1 }

TForm1 = class(TForm)

Button1: TButton;

Edit1: TEdit; Edit2: TEdit; Edit3: TEdit;

Label1: TLabel; Label2: TLabel; Label3: TLabel;

procedure Button1Click(Sender: TObject);

private

{ private declarations }

public

{ public declarations }

end;

var

Form1: TForm1;

implementation

{$R *.lfm}

{ TForm1 }

function BesselI0(x, eps: Double): Double;

var

...

begin

...

end;

procedure TForm1.Button1Click(Sender: TObject);

var

x, y, eps: double;

begin

x:= StrToFloat(Edit1.Text);

eps:= StrToFloat(Edit2.Text);

y:= BesselI0(x, eps);

Edit3.Text:= FloatToStr(y);

end;

end.

Оконное приложение в среде Visual C++, фрагмент кода:

double BesselI0(double x, double eps)

{

int i, N;

double T, A, B, R, x2;

x2 = (x / 2.0)*(x / 2.0);

A = x2;

N = 0;

B = x2 / ((double)N + 2.0) / ((double)N + 2.0);

do

{

N++;

A *= B;

B = x2 / ((double)N + 2.0) / ((double)N + 2.0);

R = A / (1 - B);

}

// while (!(B < 1 && R < eps));

while (B >= 1 || R >= eps);

T = 1.0;

for (i = N; i >= 1; i--)

T = 1.0 + x2 / ((double)i * (double)i) * T;

return T;

}

private: System::Void button1_Click(System::Object^ sender, System::EventArgs^ e)

{

double x;

x = System::Convert::ToDouble(textBox1->Text);

double eps;

eps = System::Convert::ToDouble(textBox2->Text);

double y;

y = BesselI0Aux(x, eps);

textBox3->Text=System::Convert::ToString(y);

}

При решении сложных задач программирования эти задачи разбиваются на более простые подзадачи. Каждая из подзадач, в свою очередь, может быть разбита на еще более простые подзадачи, и т.д. Если задача в ходе такого последовательного разбиения свелась (необязательно за один шаг) сама к себе самой, имеет место рекурсия.

Если задача сводится к себе, и еще раз к себе, и так далее, то количество обращений к себе должно быть конечным.

Каждое очередное сведение задачи к себе должно приближать задачу к тривиальному случаю. В тривиальном случае задача решается по алгоритму, который более не сводит задачу к себе.

Рекурсия используется во множестве стандартных алгоритмов. Далее, в курсе лекций, тема «Рекурсивные алгоритмы» будет возобновляться многократно.

Пример.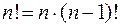

Применяя сведение задачи к себе n раз, можно «дойти» до тривиального случая – до значения 0!, а оно равно 1.

Пример 2.

Применение такого сведения задачи к себе приводит к «зацикливанию».

Числа Фибоначчи 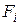выражаются «сами через себя» при 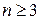, но выражаются явно (дают тривиальный случай) при и :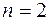

, , , .

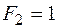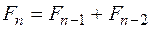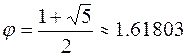, – Golden Ratio.

Сумма убывающей геометрической прогрессии

, ,

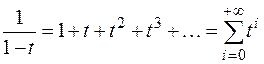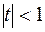есть функциональный (а именно, степенной, по степеням переменной ) ряд с коэффициентами 1, 1, ….

Полиномы Фибоначчи 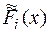являются коэффициентами разложения в степенной ряд функции

, .

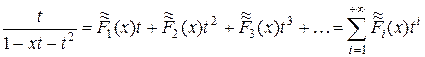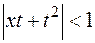Полиномы Фибоначчи 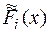выражаются «сами через себя» при 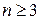, но выражаются явно (дают тривиальный случай) при и :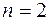

, ,

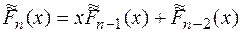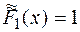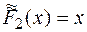
Связь с числами Фибоначчи: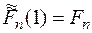

Пример рекурсивной функции

function Fib(n: integer; x: double): double;

Дата добавления: 2014-01-04