Теоретическое введение. Сверхтонкая структура (СТС) спектральных линий

СПЕКТРАЛЬНЫХ ЛИНИЙ, СПИНА ЯДРА ТАЛЛИЯ

ИЗУЧЕНИЕ СВЕРХТОНКОЙ СТРУКТУРЫ

7.1. Цель и содержание работы: изучение сверхтонкой структуры спектральных линий с помощью интерферометре Фабри-Перо и определение спина ядра таллия.

7.2. Аппаратура: Спектрограф ИСП-28, интерферометр Фабри-Перо ИТ-51,лампы ВСБ-2 с парами ртути и таллия, блок питания ППБЛ-3.

При исследовании с помощью спектральных приборов высокой разрешающей силы линии большинства элементов обнаруживают сложную структуру, значительно более узкую, чем мультиплетная (тонкая) структура линий. Ее возникновение связано с взаимодействием магнитных моментов ядер с электронной оболочкой, приводящим к сверхтонкой структуре уровней и с изотопическим сдвигом уровней.

Магнитные моменты ядер связаны с наличием у них механических моментов импульса (спинов). Спин ядра – квантуется по общим правилам квантования механических моментов. Если массовое число ядра А является четным, квантовое число спина I - целое, при нечетном А число I - полуцелое. Большая группа так называемых четно-четных ядер, имеющих четное число как протонов, так и нейтронов, обладает нулевым спином и нулевым магнитным моментом. Спектральные линии четно-четных изотопов не имеют сверхтонкой структуры. Остальные изотопы обладают отличными от нуля механическими и магнитными моментами.

По аналогии с магнитными моментами, создаваемыми в атомах электронами 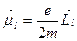и , магнитный момент ядра 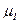может быть представлен в виде

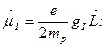(7.1)

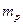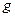где – масса протона, – так называемый – фактор ядра, учитывающий структуру ядерных оболочек (по порядку величины он равен единице). Единицей измерения ядерных моментов служит ядерный магнетон:

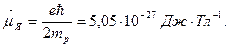(7.2)

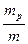Ядерный магнетон в =1836 раз меньше магнетона Бора . Малая величина магнитных моментов ядер по сравнению с магнитными моментами электронов в атоме объясняет узость сверхтонкой структуры спектральных линий, составляющей по порядку величины от мультиплетного расщепления.

Энергия взаимодействия магнитного момента ядра с электронами атома равна

(7.3)

где 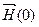– напряженность магнитного поля, создаваемого электронами в точке, где находится ядро.

Расчеты приводят к формуле

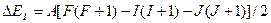(7.4)

Здесь А – некоторая постоянная для данного уровня величина, F – квантовое число суммарного момента импульса ядра и электронной оболочки

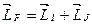(7.5)

которое принимает значения

F=J+I, J+I—1,…, |J—I|. (7.6)

Сверхтонкое расщепление увеличивается с ростом заряда ядра Z, а также с увеличением степени ионизации атома приблизительно пропорционально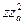, где 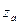заряд атомного остатка. Если у легких элементов сверхтонкая структура крайне узка (порядка сотых долей 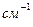), то для тяжелых элементов, таких, как Hg, T1, Pb, Bi, она достигает величины в случае нейтральных атомов и нескольких 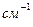в случае ионов.

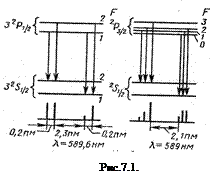
В качестве примера на рис. 7.1 изображена схема сверхтонкого расщепления уровней и линий резонансного дублета натрия (переход ). Натрий (Z=11) имеет единственный стабильный изотоп с массовым числом А=23. Ядро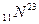 относится к группе нечетно-четных ядер и обладает спином I=3/2. Магнитный момент ядра равен 2.217 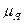. Общий нижний уровень обеих компонент дублета 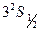расщепляется на два сверхтонких уровня с F=1 и 2. Уровень на четыре подуровня (F=0, 1, 2, 3). Величина расщепления уровня 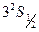равняется 0,095 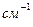. Расщепление верхних уровней намного меньше: для уровня 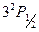оно равно 0,006 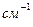, полное расщепление - уровня составляет 0,0035 .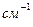

Исследования сверхтонкой структуры спектральных линий позволяют определять такие важные величины, как механические и магнитные моменты ядер.

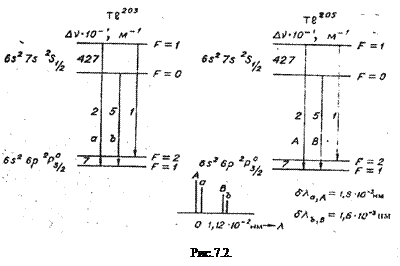
Примером определения значения спина ядра непосредственно по числу компонент служит вычисление ядерного момента таллия 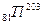и 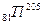по структуре линии с =535,046 нм. Полная картина расщепления уровней 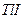представлена на рис.7.2. Таллий имеет два изотопа: 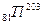и 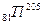, процентное содержание которых в естественной смеси составляет: 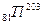–29,50% и 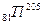– 70,50%. Линии обоих изотопов таллия испытывают изотопическое смещение, соответственно равное 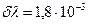и 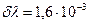нм. Для обоих изотопов спин ядра I=1/2. По схеме расщепления нужно ожидать, что линия таллия с 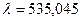нм, возникающая при переходе с уровня 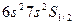на уровень , состоит из трех компонент сверхтонкого расщепления с отношением интенсивностей 2:5:1, так как уровень 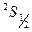состоит из двух подуровней с расстоянием между подуровнями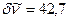 , а уровень 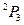также расщепляется на два подуровня. Расстояние между подуровнями ничтожно мало, поэтому спектроскопические наблюдения обнаруживают лишь две компоненты сверхтонкого расщепления для каждого изотопа в отдельности, расположенные на расстоянии 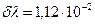нм (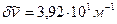). По числу компонент видно, что спин ядра таллия I =1/2, так как при J = 1/2 число компонент 2I+1 =2. Квадрупольный момент Q = 0. Это свидетельствует, что расщепление терма очень мало и спектроскопическим способом не разрешается. Аномально-узкое расщепление терма объясняется тем, что он испытывает возмущение со стороны конфигурации 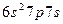. Общее число компонент этой линии равно четырем. Компоненты А и В принадлежат более распространенному изотопу 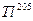, а компоненты 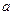и b более редкому 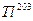. Обе группы компонент сдвинуты относительно друг друга на 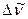, причем более тяжелому изотопу соответствует сдвиг в фиолетовую сторону спектра. Измерение отношения интенсивностей компонент А: или В: b позволяет определить содержание изотопов в естественной смеси.

7.4. Описание установки.

СТС спектральных линий можно наблюдать только при использовании приборов высокой разрешающей силы, например, интерферометра Фабри-Перо (ИФП). ИФП является прибором с узким спектральным интервалом, (например, свободный спектральный интервал для λ=500 нм в ИФП с расстоянием между зеркалами t=5 мм составляет Δλ=0,025 нм, в пределах этого интервала Δλ можно исследовать тонкую и сверхтонкую структуру). Как правило, ИФП используют в сочетании со спектральным прибором, для предварительной монохроматизации. Эта монохроматизация может быть осуществляться или до входа светового потока в интерферометр, или после прохождения через интерферометр.

Оптическая схема для исследования СТС спектральных линий приведена на рис. 7.3.

Источник света 1 (высокочастотная безэлектродная лампа ВСБ с парами металлов) проектируется линзой 2 (F =75мм) на ИФП (3). Интерференционная картина, локализованная в бесконечности, в виде колец проектируется ахроматическим конденсором 4 (F=150мм) в плоскость входной щели 5 спектрографа (6,7,8-коллиматор, призма Корню, камерный объектив спектрографа). Центральная часть концентрических колец вырезается щелью (5) спектрографа и изображение картины переносится в фокальную плоскость 9, где регистрируется на фотопластинку. В случае линейчатого спектра картина будет представлять собой спектральные линии, пересеченные по высоте интерференционными максимумами и минимумами. Такую картину можно наблюдать визуально со стороны кассетной части в лупу. При правильной юстировке ИТ картина имеет симметричный вид (рис.7.4.).

Дата добавления: 2014-01-04