Порядок выполнения работы. Маятник Обербека монтируется на блоке 11, закрепленном на стойке 10 модуля ЛКМ–3 (рис

Описание установки

Маятник Обербека монтируется на блоке 11, закрепленном на стойке 10 модуля ЛКМ–3 (рис. 3). К блоку радиусом 25 мм прикрепляют нить, к концу которой подвешивают наборный груз массой т = 100 ÷ 200 г. На ось блока через среднее отверстие надевают стержень 12 и закрепляют его пластиковым фиксатором 13. Вращая стержень, накручивают на блок нить и поднимают груз так, чтобы он не касался стержня. При опускании груза нить приведет во вращательное движение стержень. После полного раскручивания нити стержень, продолжая вращательное движение, накрутит нить на блок и поднимет груз. При этом вращательное движение прекратится – система перейдет в начальное состояние.

Время опускания и подъема груза (период колебаний маятника Обербека) зависит от многих параметров установки: длины нити, массы груза т, момента инерции стержня и блока, радиуса блока (от сил трения, толщины и массы нити, которыми мы в данной работе пренебрегаем).

Задание I. Определение момента инерции стержня и блока

Подготовьте измерительную систему ИСМ–1 к работе: подключите датчик угла поворота блока к разъему 1 на задней стенке прибора, переключатель 1 поставьте в положение «К1», переключатель 4 – в положение «:1», переключатель 5 – в положение «однокр», переключатель 8 – в положение «+» или «–», переключатель 9 – в среднее положение. Включите питание модуля.

Рис. 3. Маятник Обербека на модуле ЛКМ-3

1. Закрепите конец нити на блоке так, чтобы нить не мешала креплению стержня и могла накручиваться на большой блок

(R = 25 мм). Укрепите стержень на оси блока, пропустив ось блока через середину стержня, и зафиксируйте его пластиковым фиксатором.

2. Накрутите нить на блок и прикрепите наборный груз т к свободному концу нити.

3. Поверните блок 11 со стержнем 12 так, чтобы прорезь блока совпала с нулевым делением шкалы и добейтесь срабатывания индикатора датчика угла поворота 3. Нажмите кнопку 7 «готов» и осторожно, без толчка, отпустите маятник, который под действием груза придет в движение. После одного полного оборота сработает датчик угла поворота блока и на индикаторе появится значение времени поворота в секундах или миллисекундах в зависимости от положения переключателя 2. Время и массу груза занесите в табл. 1.

Таблица 1

№ п/п	т	T	I	I – < I >	(I – < I >)^2
…
…
среднее	―	―		―	―
сумма	―	―	―	―

4. Рассчитайте по формуле (16) суммарный момент инерции I стержня блока.

5. Рассчитайте абсолютную и относительную погрешности измерения момента инерции I системы по методу Стьюдента для прямых измерений. Результат запишите в стандартном виде:

кг-м²; ε =...% при α = 0,95.

Задание II. Измерение момента инерции маятника Обербека в зависимости от положения грузов на стержне

1. Закрепите на стержне 12 симметрично относительно оси вращения два круглых груза 14 (см. рис. 3). Занесите в табл. 2 расстояние от оси вращения до центра грузов r, и массу наборного груза т.

2. Измерьте момент инерции системы так, как это описано в задании I. Данные занесите в табл. 2.

Таблица 2

№ п/п	т	T	r	r ^2	I

Перемещая грузы 14 по стержню 12, повторите измерения момента инерции I для всех положений грузов (расстояние между отверстиями на стержне d = 20 мм).

Постройте график зависимости момента инерции I от квадрата расстояния от оси вращения до центра грузов r ².

Контрольные вопросы

1. Дайте определение динамических характеристик вращательного движения: момента силы М, момента инерции I, момента импульса L.

2. Вывод основного уравнения динамики вращательного движения.

3. Вывод основной рабочей формулы (16).

4. Выражения для момента инерции материальной частицы, стержня, диска относительно оси, проходящей через центр масс. Как определяется момент инерции относительно произвольной оси? Теорема Штейнера.

5. Провести аналитический расчет момента инерции маятника Обербека. Как рассчитать период колебаний маятника Обербека?

Задания для отчета по лабораторной работе

1. Два маленьких шарика массой m = 10 г каждый скреплены тонким невесомым стержнем длиной l = 20 см. Определить момент инерции 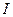системы относительно оси, перпендикулярной стержню и проходящей через центр масс.

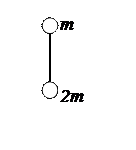
2. Два шара массами m и 2m (m = 10 г) закреплены на тонком невесомом стержне длиной l = 40 см так, как это указано на рис. 4. Определить момент инерции 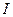системы относительно оси, перпендикулярной стержню и проходящей через его конец. Размерами шаров пренебречь.

3. Два шара массами 2m и m (m = 20 г) закреплены на тонком невесомом стержне длиной l = 1 м так, как это показано на рис. 5 Определить момент инерции 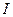системы относительно оси, перпендикулярной стержню и проходящей через его конец. Размерами шаров пренебречь.

Рис. 4 (к задаче 2) Рис. 5 (к задаче 3)

4. Определить момент инерции трехатомной молекулы H₂O (рис. 6) относительно оси y, проходящей через центр масс молекулы. Межъядерное расстояние AB обозначено d = 0,097 нм, α = 104^о30' .

5. Определить момент инерции трехатомной молекулы SO₂ (рис. 6) относительно оси x, проходящей через центр масс молекулы

(d = 0, 145 нм, α = 124^о).

Рис. 6 (к задаче 6)

6. Определить момент инерции тонкого однородного стержня длиной l = 30 см и массой m = 100 г относительно оси, перпендикулярной стержню и проходящей через точку, отстоящую от конца стержня на 1/3 его длины. Определить момент инерции тонкого однородного стержня длиной l = 60 см и массой m = 100 г относительно оси, перпендикулярной ему и проходящей через точку стержня, удаленную на

a = 20 см от одного из его концов.

7. На концах тонкого однородного стержня длиной l и массой 3 m прикреплены маленькие шарики массами m и 2 m. Определить момент инерции такой системы относительно оси, перпендикулярной стержню и проходящей через точку, лежащую на середине стержня (рис. 7).

Рис. 7 (к задаче 7)

8. Вычислить момент инерции J проволочного прямоугольника со сторонами a = 12 см и b = 16 см относительно оси, лежащей в плоскости прямоугольника и проходящей через середины малых сторон. Масса равномерно распределена по длине проволоки с линейной плотностью 0,1 кг/м.

9. Определить момент инерции проволочного равностороннего треугольника со стороной a = 10 см относительно: оси, лежащей в плоскости треугольника и проходящей через его вершину и середину противоположной стороны.

10. Определить момент инерции кольца массой m = 50 г и радиусом R = 10 см относительно оси, касательной кольцу.

11. Диаметр диска d = 20 см, масса m = 800 г. Определить момент инерции диска относительно оси, проходящей через середину одного из радиусов перпендикулярно плоскости диска.

12. Найти момент инерции плоской однородной прямоугольной пластины массой m = 800 г относительно оси, совпадающей с одной из ее сторон, если длина a другой стороны равна 40 см.

13. Определить момент инерции тонкой плоской пластины со сторонами a = 10 см и b =20 см относительно оси, проходящей через центр масс пластины параллельно большей стороне. Масса пластины равномерно распределена по ее площади с поверхностной плотностью 1,2 кг/м².

14. В однородном диске массой m = 1 кг и радиусом R = 30 см вырезано круглое отверстие диаметром d =20 см, центр которого находится на расстоянии l = 15 см от оси диска (рис. 8). Найти момент инерции полученного тела относительно оси, проходящей перпендикулярно плоскости диска через его центр.

15. На однородный сплошной цилиндр массой M и радиуса R плотно намотана легкая нить, к концу которой прикреплен груз массой m (рис.9). В момент времени t = 0 система пришла в движение. Пренебрегая трением в оси цилиндра, найти зависимость от времени модуля угловой скорости цилиндра.

Рис. 8 (к задаче 14) Рис. 9 (к задаче 15)

16. Через неподвижный блок массой m = 0,2 кг перекинут шнур, к концам которого подвесили грузы массами m ₁ = 0,3 кг и m ₂ = 0,5 кг. Определить силы T ₁ и T ₂ натяжения нити по обе стороны блока во время движения грузов, если масса блока равномерно распределена по ободу.

17. Через блок, имеющий форму диска, перекинут шнур. К концам шнура привязали грузы массой m ₁ = 100 г и m ₂ = 110 г. С каким ускорением будут двигаться грузы, если масса блока m = 400 г. Трение при вращении блока ничтожно мало.

18. Два тела массами m ₁ = 0,25 г и m ₂ = 0,15 г связаны тонкой нитью, переброшенной через блок (рис. 10). Блок укреплен на краю горизонтального стола, по поверхности которого скользит тело массой m₁.

С каким ускорением движутся тела, и каковы силы T ₁ и T ₂ натяжения нити по обе стороны блока? Коэффициент трения µ тела о поверхность стола равен 0,2. Масса m блока равна 0,1 г, и ее можно считать равномерно распределенной по ободу. Массой нити и трением в подшипниках оси блока пренебречь.

19. Однородный сплошной цилиндр массой m = 1 кг висит в горизонтальном положении на двух намотанных на него невесомых нитях (рис.11). Цилиндр отпускают без толчка. а) За сколько времени t цилиндр опустится на расстояние y =50 см? б) Какое натяжение F испытывает при опускании цилиндра каждая из нитей?

Рис. 10 (к задаче 18) Рис. 11 (к задаче 19)

Дата добавления: 2014-01-04