Работа электростатического поля

Заряд q₀, находящийся в точке поля с потенциалом 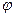, обладает потенциальной энергией W = q₀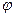. Следовательно, работа сил поля над зарядом q₀ может быть выражена через разность потенциалов.

A_1-2 = W₁ – W₂ = q₀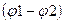

Таким образом, работа, совершаемая над зарядом силами поля, равна произведению величины заряда на разность потенциалов в начальной и конечной точках. Если заряд из точки с потенциалом 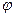удаляется на бесконечность (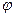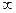= 0), работа сил поля будет равна A_1-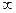= q₀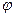, то есть потенциал численно равен работе, которую совершают силы поля над единичным положительным зарядом при удалении его из данной точки на бесконечность.

В СИ за единицу потенциала, называемую вольтом (В), принимается потенциал в такой точке, для перемещения, в которую из бесконечности заряда в 1 Кл нужно совершить работу в 1 Дж.

1= .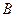

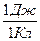Расчет электростатических полей методом суперпозиции.

Опыт показывает, что сила, с которой система зарядов действует на некоторый не входящий в систему заряд, равна векторной сумме сил, действующий на данный заряд со стороны каждого из зарядов системы в отдельности.

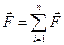_i

Отсюда вытекает, что напряженность поля системы зарядов в данной точке равна векторной сумме напряженности полей, создаваемых каждым зарядом системы в данной точке по отдельности.

_i, а 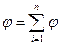_i. (2.10)

Это утверждение носит название принципа суперпозиции (наложения) электрических полей.

Принцип суперпозиции позволяет вычислить напряженность и потенциал поля любой системы зарядов. Разбив протяженные заряды на достаточно малые доли dq, любую систему зарядов можно свести к совокупности точечных зарядов. Вклад каждого из таких зарядов в результирующее поле вычисляют по формулам:

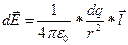_r ; ,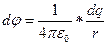

А процесс суммирования заменяется интегрированием по объему протяженного заряда.

Электрическое поле можно описать, указав для каждой точки величину и направление вектора 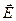. Совокупность этих векторов образует поле вектора напряженности, которое можно наглядно представить с помощью линий напряженности (силовых линий). Линии напряженности проводят таким образом, чтобы касательная к ним в каждой точке совпадала с направлением вектора 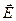. Густота линий выбирается так, чтобы количество линий N, пронизывающих единицу поверхности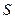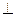, перпендикулярной к линиям площадки, было равно числовому значению вектора 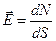. Линии 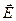поля точечного заряда представляют собой совокупность радикальных прямых, направленных от заряда, если он положителен, и к заряду, если он отрицателен.

Электрическое поле изображают также с помощью эквипотенциальных поверхностей – поверхностей равного потенциала. В каждой точке поля линия напряженности перпендикулярна к эквипотенциальной поверхности. Для поля точечного заряда эквипотенциальные поверхности представляют собой систему концентрических сфер.

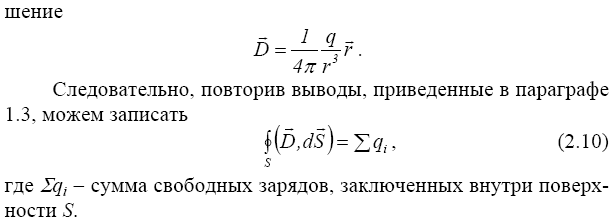
Дата добавления: 2014-01-04