
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Конспект лекций. Ты мне силы даёшь, чтоб забыться
|
|
|
|
ХИМИЯ
Логика
Гр.
Гусева Анастасия
Гусева Анастасия
Роман.
Ты мне силы даёшь, чтоб забыться.
И с тобою счастливая я.
Мне такое могло только сниться.
Это миф, это сказка моя!
Я в руках твоих нежных растаю,
Окунусь в сладких губ поцелуй...
Ты со мною, я верю, я знаю!
Так балуй же меня ты, балуй!
Вряд ли в жизни найду я такого,
Чтобы был интересней тебя.
Разве может быть что-то плохого,
Что ты дорог вдруг стал для меня?
О любимом забуду с тобою.
И печаль, и обиду, ту боль.
И прошу я тебя, будь со мною.
Не ломай это счастье! Не тронь!
Без тебя мне опять будет больно.
Все барьеры и трудности вновь.
Я молю, прекрати всё, довольно!
Ты не знаешь, как губит любовь.
Вопросы к экзамену по «Русской литературе ХХ века (1890-1930-е гг.)
- Общая характеристика литературы кона XIX – начала ХХ в. Исторические условия развития. Периодизация. Основные эстетические пласты.
- Русский символизм: истоки, философско-эстетические концепции. Содержание теоретических документов. Поэтическая практика русского символизма (Д. Мережковский, К. Бальмонт, Ф. Сологуб, В. Брюсов и др.).
- Акмеизм: истоки, философско-эстетические концепции. Содержание теоретических документов акмеистов. Поэтическая практика Акмеистов (Н. Гумилев, А. Ахматова, О. Мандельштам и др.).
- Футуризм: истоки, философско-эстетические концепции. Итальянский футуризм. Основные эстетические программы разных группировок. Поэтическая практика русского футуризма (В. Хлебников, И. Северянин и др.).
- А. Блок. Философско-эстетические позиции. Периодизация творчества. Поэмы А. Блока «Соловьиный сад», «Возмездие».
- Основные мотивы и образы в раннем творчестве В. Маяковского. Философско-эстетическая программа.Поэма В. Маяковского «Облако в штанах». Основные философско-эстетические концепции.
- А.И. Куприн: основные тематические пласты и их содержание.
- Реалистические и нереалистические тенденции в рассказах Л. Андреева 90-900-х годов («Баргамот и Гараська», «Петька на даче», «Мысль», «Бездна», «Красный смех», «Рассказ о семи повешенных», «Жизнь Василия Фивейского», «Иуда Искариот»).
- Л. Андреев – создатель «панпсихического» театра.(«К звездам», «Жизнь Человека», «Савва», «Собачий вальс»).
- Философско-эстетические воззрения И. Бунина. Основные тематические пласты.
- М. Горький. Философско-эстетическая концепция в ранних произведения Горького.Жанр социально-психологического романа в творчестве раннего Горького. Проблема героя («Фома Гордеев», «Трое»).
- М. Горький «На дне»: как социально-философская драма. История создания. Философско-эстетические концепции.
- Творчество А. Блока после 1917 г. Поэма А. Блока «Двенадцать» - музыкальный образ эпохи. Особенности сюжета и композиции.
- Основные тенденции и этапы послеоктябрьского творчества Вл. Маяковского. Лирический эпос Вл. Маяковского.
- Сатира Вл. Маяковского: основные этапы, способы сатирической типизации. Пьесы В. Маяковского «Клоп» и «Баня».
- Человек и история в романе М. Горького «Дело Артамоновых».
- «Жизнь Клима Самгина» - «движущая панорама десятилетий». Историческое и общечеловеческое в произведении.
- Литературный процесс 1917-1930-х гг.: факторы развития, специфические черты, проблематика изучения, периодизация.
- Литературные группировки 20-х годов: ЛЦК, ЛЕФ, РАПП, «Серапионовы братья», «Перевал», ОБЭРИУ.
- Эволюция и интеллигенция в трилогии А. Толстого «Хождение по мукам».
- Основные этапы творческой эволюции С. Есенина. Поэтический мир С. Есенина: особенности поэтического образа, концепция поэтического творчества.
- Революция и гражданская война в творчестве М. Шолохова («Донские рассказы», «тихий Дон»).
Логика – это нормативная наука о формах и приемах интеллектуальной познавательной деятельности, осуществляемой с помощью языка.
Познание – процесс отражения в человеческом мозге некоторой информации. Познание бывает:
· Чувственное
· Рациональное (вербальность, абстрактность, целенаправленность)
Язык – знаковая система, предназначенная для обработки, фиксирования, передачи и хранения информации.
Естественный язык создается в историческом процессе, основная задача – общение.
Искусственный язык создается целенаправленно для решения определенных задач.
Объектный язык – это тот язык, которым ведется какое-либо исследование.
Метаязык – тот язык, который используется для изучения другого языка.
Знак – это объект, который выступает в качестве представителя какого-либо другого объекта. Характеристики знака:
· Значение – тот самый объект, представителем которого является данный знак
· Смысл – информация о представляемом объекте, которую несет сам знак или которая связывается с ним в процессе человеческого общения или познания.
С точки зрения
1. значения знаки бывают:
· пустые – на заданной предметной области нет ни одного объекта, представителем которого выступал бы этот знак
· непустые – на заданной предметной области знак выступает представителем хотя бы одного объекта
2. смысла знаки бывают:
· описательные – знак сам несет информацию о представляемом объекте
· неописательные – информация связывается в процессе человеческого общения/познания
Семиотика – наука о знаках. Делится на:
· Синтактика – изучает отношения между самими знаками
· Семантика – изучает отношения между знаком и представляемым им объектом
· Прагматика – изучает отношения между знаком и его интерпретатором
Классическая теория высказываний (КЛВ)
КЛВ – логическая теория, содержащая один тип нелогических символов – пропозициональные переменные, и один тип логических символов – пропозициональные связки.
Высказывание – повествовательное предложение, о котором однозначным образом можно утверждать, что оно истинное или ложное.
Язык КЛВ:
· Алфавит
o p, q, r, s, p1, … - пропозициональные переменные
o ˥, &, V,  ,
,  , V – пропозициональные связки
, V – пропозициональные связки
o), (- технические символы
˥ - отрицание (не)
& - конъюнкция (и)
V – дизъюнкция (или)
V – строгая дизъюнкция (либо, либо)
 - импликация (если, то)
- импликация (если, то)
 - эквивалентность (тогда и только тогда, если и только если)
- эквивалентность (тогда и только тогда, если и только если)
· Определение ППФ
o Всякая пропозициональная переменная – это ППФ
o Если A – ППФ, то ˥A – так же ППФ
o Если A и B – ППФ, то (A&B), (AVB), (A V B), (A B), (A
B), (A B) – ППФ
B) – ППФ
o Ничто иное не является ППФ
Пример: если гора не идет к Магомету, то Магомет идет к горе.
P – гора идет к Магомету
Q – Магомет идет к горе
˥P Q
Q
Таблицы истинности
1 = истинно
0 = ложно
| A | B | A&B (*) | AVB (+) | A V B (-) | A B (≤) B (≤)
| A B (=) B (=)
|
Всего строк 2n где n – это число различных пропозициональных переменных, вошедших в формулу.
Результирующий столбец таблицы находится под главным знаком формулы.
Виды формул:
1. Тождественно-ложные (противоречия) – если и только если в каждой строке результирующего столбца она принимает значение «ложь» (0).
2. Выполнимые – если и только если она принимает значение «истина» хотя бы в одной строке результирующего столбца.
3. Собственно выполнимая – если и только если в каждой строке результирующего столбца она принимает значение «истина»
3 закона КЛВ
1. Закон тождества A A
A
2. Закон исключенного третьего AV˥A
3. Закон противоречия ˥(A&˥A)
4. Закон контрпозиции (A B)
B)  (˥B
(˥B ˥A)
˥A)
Отношения между формулами:
· Фундаментальные (основные) – формулы некоторого множества Г находятся в отношении совместимости по ложности если и только если хотя бы в одной строке их совместной таблицы они одновременно принимают значение ложь
· Вспомогательные – формулы некоторого множества Г находятся в отношении совместимости по истинности если и только если хотя бы в одной строке их совместной таблицы они одновременно принимают значение «истина»
· Из множества формул Г логически следует формула B (Г|=B) если и только если в их совместной таблице не находится такой строки, в которой все формулы из Г одновременно принимают значение «истина», а формулы B – ложь.
· Формулы A и B находятся в отношении контрарности если и только если они совместимы по ложности и не совместимы по истинности
· Формулы A и B находятся в отношении субконтрарности если и только если они совместимы по истинности и не совместимы по ложности
· Формулы A и B находятся в отношении контрадиктности если и только если они не совместимы по ложности и не совместимы по истинности или не совместимы по ложности
· Формула B находится в отношении подчинения к формуле A если и только если из формулы A|=B, а из формулы B не следует A
· Формулы A и B находятся в отношении эквивалентности если и только если A|=B и B|=A
· Формулы A и B находятся в отношении независимости если и только если они совместимы по истинности, совместимы по ложности и не следуют друг из друга
Классическая логика предикатов (КЛП)
Язык КЛП:
· Алфавит
o a, b, c, d, a1 … - индивидуальные константы (имена собственные)
o x, y, z, x1… - индивидуальные переменные (имена нарицательные)
o f′, g′ - функторы
o P1, Q1, R1, S1, R2 – предикаты
o ˥, &, V,  - пропозициональные связки
- пропозициональные связки
o Ǝ, 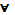 - кванторы
- кванторы
o), (- технические символы
Предметные функторы – термины, с помощью которых в языке представляются предметные функции (с помощью предметных функторов – выражения).
Пример: Аристотель – a
отец Аристотеля - f′(a)
Предикаты – термины, выражающие в языке предметно-истинностные функции (свойства и отношения)
· Определение правильно построенного терма:
o Всякая индивидуальная константа – это ППТ
o Всякая индивидуальная переменная – это ППТ
o Если Фn – n-местный предметный фактор, а t₁, t₂, t₃, …, tn – правильно построенные термы, то Фn (t₁, t₂, t₃, …, tn) – это ППТ
o Ничто иное не является ППТ
· Определение правильно построенной формулы (ППФ)
o Если П - n-местный предикат, а t₁, t₂, t₃, …, tn – это ППТ, тогда П n(t₁, t₂, t₃, …, tn) – ППФ
o Если A – ППФ, то ˥A – ППФ
o Если A и B – ППФ, то (A&B), (AVB), (A B) – ППФ
B) – ППФ
o Если A и B – ППФ, α – индивидуальная переменная, то ƎαA, 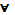 αA – ППФ
αA – ППФ
o Ничто иное не является ППФ
Пример:
4 = a 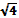 - f1(a)
- f1(a)
5 = b 4+5 - g2(a, b)
√ = f1 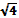 +5 - g2(f1(a), b)
+5 - g2(f1(a), b)
+ = g2 (4+4)+(5+5) - g2(g2(a, a), g2(b, b))
В формулах вида 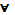 αA и ƎαA формула A называется областью действия квантора по переменной α.
αA и ƎαA формула A называется областью действия квантора по переменной α.
В произвольной формуле каждая индивидуальная переменная имеет некоторое число вхождений.
Вхождение индивидной переменной в некоторую формулу называется связанным, если оно следует непосредственно за квантором или находится в области действия квантора по данной переменной, в противном случае вхождение переменной в формулу называется свободным.
Индивидная переменная называется свободной в некоторой формуле, если существует по крайней мере одно свободное вхождение в эту формулу.
Терм называется замкнутым, если он не содержит в своем составе ликвидных переменных.
Формула называется замкнутой, если никакая индивидная переменная не является в ней свободной.
1. Закон подчинения
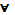 αA
αA ƎαA
ƎαA
2. Закон противоречия
˥ (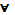 αA&˥
αA&˥ 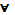 αA)
αA)
3. Закон непустоты предметной области
4. ƎαA V ˥ ƎαA
Рассуждение – это логическая процедура последовательного перехода от одних высказываний, принятых в качестве посылок, к другим высказываниям. Каждый шаг такого перехода осуществляется по какому-либо правилу вывода. Последняя формула рассуждения – заключение.
Дедуктивное рассуждение – рассуждение, в котором между высказываниями, принятыми в качестве исходных, и заключением сохраняются отношения логического следования.
Аналитические таблицы (АТ)
Логические теории бывают разрешимыми (КЛВ) и неразрешимыми (КЛП).
Теория называется разрешимой если существует эффективная процедура (алгоритм), позволяющая для любой формулы языка данной теории в конечное число шагов решить вопрос о том, является ли эта формула законом теории или нет. В противном случае теория называется неразрешимой.
Метод от противного: |=A допустим: ˥A
Особенности АТ
1. Аналитическая таблица состоит из отмеченных формул (к которым добавили знак t или f)
2. АТ двумерна – это дерево отмеченных формул. Цепь АТ – последовательность, без пропусков, вхождений отмеченных формул, начинающаяся с самой верхней формулы таблицы (кроме дерева) до 1 из самых нижних формул.
Таблица, соответствующая одному шагу рассуждений от противного, содержит одну начальную цепь формул и выражает исходные допущения данного рассуждения (т. е. антитезис).
Правила редукции:
| t (A&B) | f (A&B) | |
| t A, t B | f A | f B |
| t (A V B) | f (A V B) | |
| t A | t B | f A, f B |
t (A  B) B)
| f (A  B) B)
| |
| f A | t B | t A f B |
| t ˥A | f ˥A | |
| f A | t A | |
t 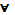 αA (α) αA (α)
| f 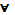 αA (α) αA (α)
| |
| t A (k) где A (k) – результат замены всех свободных вхождений α в A на произвольной замкнутый терм k | f A (k) где A (k) – результат замены всех свободных вхождений α в A на произвольной замкнутый терм k, который не содержится в отмеченных формулах цепи | |
| t ƎαA (α) | f ƎαA (α) | |
| t A (k) | f A (k) |
Аналитическая таблица – конечное или бесконечное дерево отмеченных формул. Цепь называется замкнутой, если в ней встречается две отличные формулы tC и fC. АТ называют замкнутой, если каждая ее цепь является замкнутой.
Формула A является общезначимой (|=A) если и только если существует замкнутая аналитическая таблица, начальная цепь которой начинается с отмеченной формулы fA.
A₁, A₂, A₃, …, An |=B если и только если существует замкнутая аналитическая таблица, начальная цепь которой начинается с отмеченных формул tA₁,t A₂,t A₃, …,t An fB.
Натуральные исчисления. Исчисления высказываний.
Правила редукции (вывода):
1. &в: 
2. Vв: 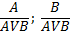
3.  в:
в: 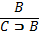 (последняя посылка вывода)
(последняя посылка вывода)
4. &и: 
5. Vи: 
6. ˥в: 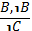
7.  и:
и: 
8. ˥и: 
Вывод – это непустая конечная последовательность формул C₁, C₂, C₃, …, Cn, удовлетворяющая следующим условиям:
1. Каждая Ci является либо посылкой, либо получена из предыдущей формулы по одному из правил вывода
2. Если в выводе принимались правила  B или ˥B, то все формулы, начиная с последней посылки вплоть до результата применения этого правила, считаются исключенными из вывода и не участвуют в дальнейшем построении вывода.
B или ˥B, то все формулы, начиная с последней посылки вплоть до результата применения этого правила, считаются исключенными из вывода и не участвуют в дальнейшем построении вывода.
Доказательство – вывод из пустого множества не исключенных посылок.
· B – введение импликации
˥B – введение отрицания
Силлогистика
Аристотель (384 - 322 до н. э.)
Силлогистика – это логическая теория, изучающая простые категорические атрибутивные высказывания (ПКАВ) и отношения между ними.
Состав ПКАВ:
1. Квантор
2. Термины:
· S – субъект высказывания, логическая подлежащее, тот объект, о котором идет речь
· P – предикат, логическое сказуемое, то, что говорится о субъекте, предицируется субъектом
3. Связка (есть, является, суть, -)
Пример: Все мишки любят мед
 | |||
 | |||
Виды высказываний
I. По количеству:
a. единичные – субъект которых указывает ровно на один предмет
b. множественные – субъект которых указывает более чем на один предмет
i. общие – субъект говорит обо всех элементах класса S
ii. частные – субъект говорит о некоторых (возможно, всех) элементах класса S
II. По качеству:
a. Утвердительные – перед связкой не стоит частица «не»
b. Отрицательные – перед связкой стоит частица «не»
A ff i rmo - утверждаю
N e g o – отрицаю
Отсюда обозначения (гласные буквы приведенных выше слов)
Общеутвердительные – все S являются P (a)
общеотрицательные - все S не являются P (e)
частноутвердительные - некоторые S являются P (i)
частноотрицательные - некоторые S не являются P (o)
единичноутвердительные – a является P
единичноотрицательные – a не является P
На единичные букв не хватило. Ну и ладно, всё равно это частный случай общих.
Язык силлогистики
· Алфавит
o S, P, M, S₁ - термины
o a, e, i, o – логические константы
o ~ - терминное отрицание («не»)
o ˥, &, V,  - пропозициональные связки
- пропозициональные связки
o), (- технические символы
· Определение правильно построенного терма (ППТ)
o Всякий термин является ППТ
o Если α – ППТ, то ~α – ППТ
o Ничто иное не является ППТ
· Определение ППФ
o Если α и β – это ППТ, то α a β, α i β, α e β, α o β – ППФ
o Если A – ППФ, то ˥A – ППФ
o Если A и B – ППФ, то (A&B), (AVB), (A B) – ППФ
B) – ППФ
o Ничто иное не является ППФ
Модельные схемы
I. Высказывание «Все S являются P» истинно тогда и только тогда. Когда классы S и P находятся в одном из следующих отношений: S+aP-
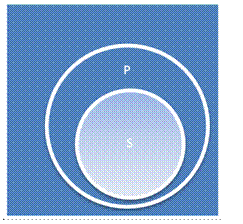

II. Высказывание «Все S не являются P» истинно тогда и только тогда, когда классы S и P находятся в одном из следующих отношений: S+eP+


III. Высказывание “Некоторые S являются P» истинно тогда и только тогда, когда классы S и P находятся в одном из следующих отношений: S-iP-




 (закрашено пересечение)
(закрашено пересечение)
IV. Высказывание «Некоторые S являются P»» истинно тогда и только тогда, когда классы S и P находятся в одном из следующих отношений: S-oP+




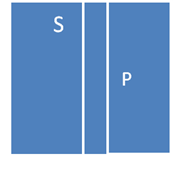 (закрашено S без P)
(закрашено S без P)
V. Высказывание «a является P»» истинно тогда и только тогда, когда классы S и P находятся в одном из следующих отношений: a+P-

VI. Высказывание «a не является P»» истинно тогда и только тогда, когда классы S и P находятся в одном из следующих отношений: a+P+

Термин считается распределенным если и только если на всех модельных схемах, которые являются условием истинности того высказывания, в которое он входит, он полностью заштрихован или полностью не заштрихован, в противном случае термин считается нераспределенным.
Единичные высказывания являются вырожденным случаем общих.
Формула A является законом силлогистики если и только если она истинна на всех модельных схемах.
Из множества формул Г логически следует формула B если и только если не найдется такой модельный схемы, на которой все формулы из Г – истинны, а формулы B ложны.
Простой категорический силлогизм (ПКС) – умозаключение, в котором на основании некоторого отношения между терминами P и M, а так же терминами S и M делают вывод о наличии определенного отношения между S и P.
Состав ПКС
S – это субъект заключения, меньший термин, посылка, в которой он находится. Называется меньшей.
P – это предикат заключения, больший термин. Посылка, в которой он находится, называется большей.
M – это средний термин, встречается в обеих посылках, но никогда в заключениях.
Модус – разновидность силлогизма, которая определяется видами высказываний, вошедших в этот силлогизм.
Силлогизм является верным если и только если он удовлетворяет следующим условиям:
I. Правило посылок:
1. Хотя бы одна посылка должна быть утвердительной.
2. Если обе утвердительные, то и заключение должно быть утвердительным.
3. Если одна из посылок отрицательная, то и заключение – отрицательное.
II. Правило терминов:
1. Средний термин должен быть распределен хотя бы в одной из посылок.
2. Если термин распределен в заключении, то он должен быть распределен и в посылке.






 Пример: Настоящие йогурты содержат живые бактерии.
Пример: Настоящие йогурты содержат живые бактерии.
Йогурты Danone содержат живые бактерии, значит, йогурты Danone – настоящие йогурты.
+PaM-
+SaM-
+SaP-
Силлогизм неверен.
Энтимема – простой категорический силлогизм, у которого пропущена одна из посылок или заключение.
Виды энтимем:
· Корректные – восстанавливаются до правильного силлогизма с истинными посылками
· Некорректные – не восстанавливаются до правильного силлогизма, или восстанавливаются, но одна из посылок – ложная

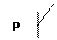

 Пример: Все кролики едят капусту. Все кролики – вегетарианцы.
Пример: Все кролики едят капусту. Все кролики – вегетарианцы.
+SaM-
+MaP-
+SaP-
Все, кто ест капусту – вегетарианцы. – ложь => энтимема некорректна
Непосредственные умозаключения – это умозаключения, в которых вывод делается на основании одной только посылки.
I. 
 Выводы по логическому квадрату – это непосредственные умозаключения со следующей структурой
Выводы по логическому квадрату – это непосредственные умозаключения со следующей структурой
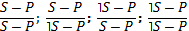
| контрарность | ||
| п о д ч и н е н и е | п о д ч и н е н и е | |
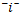
| субконтрарность | 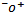
|
1. 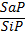
2. 
3. 
4. 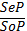
5. 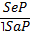
6. 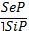
7. 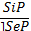
8. 
9. 
10. 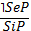
11. 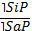
12. 
13. 
14. 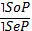
15. 
16. 
II. Обращение – это непосредственное умозаключение со следующей структурой
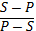

III. Превращение – это неполное умозаключение со следующей структурой
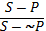
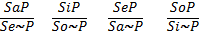
IV. Противопоставление субъекту – это непосредственное умозаключение со следующей структурой (обращение - превращение)

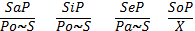
V. Противопоставление предикату – это непосредственное умозаключение со следующей структурой (превращение – обращение)
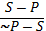
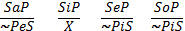
VI. Противопоставление субъекту и предикату - это непосредственное умозаключение со следующей структурой (превращение – обращение – превращение)
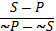

Понятие
Понимать термин – значит по любому предъявленному предмету уметь определять, подпадает ли он под данный термин или нет.
Понятие – это мысль, в которой на основании некоторого признака выделяются из универсума и обобщаются в класс все предметы, обладающие этим признаком.
αA (α) – универсалия.
Предмет α из универсума U такой, что он обладает признаком A (α).
Универсум U, по которому пробегает α, называется родом, а признак A (α) – видовым отличием.

 Пример: человек, изучающий логику
Пример: человек, изучающий логику
A (α) – содержание


 Объем W α A (α)
Объем W α A (α)
U - человек
Элемент объёма
У всякого понятия есть две основные характеристики: содержание и объем.
Содержание понятия – это тот самый признак, на основании которого предметы выделяются из универсума и обобщаются в класс.
Объем понятия – это класс всех тех предметов, которые обладают признаком, указанным в понятии.
 α A (α)
α A (α)
Объем W α A (α) содержание A (α)
Виды понятий
I. По объему:
· Пустые – пустым считается понятие, в объеме которого нет ни одного элемента
· Непустые – непустым считается понятие, в объеме которого есть хотя бы один элемент
ü Единичные – в объеме понятия ровно один элемент
ü Общие – в объеме понятия больше одного элемента
§ Универсальные – объем понятия совпадает с универсумом
§ Неуниверсальные – объем понятия меньше универсума
· Конкретные – конкретным считается понятие, элементами объема которого являются отдельные предметы или их множества
· Абстрактные – абстрактным считается понятие, элементами объема которого являются свойства, отношения или их множества.
· Собирательные - собирательным считается понятие, элементами объема которого являются множества.
· Несобирательные - несобирательным считается понятие, элементами объема которого являются отдельные предметы, свойства, отношения
II. По содержанию:
· Простые – признак не содержит логических констант (пропозициональных связок и кванторов).
· Сложные – содержат хотя бы одну логическую константу.
· Положительные – признак не содержит пропозициональные связки и отрицание.
· Отрицательные – признак содержит отрицание.
· Относительные – признак является реляционным свойством (признак не содержит свободным переменных).
· Безотносительные – признак не является реляционным свойством.
Булевы операции над объемами и понятиями.
1. Пересечения 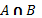
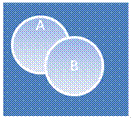

Пересечь два множества, являющиеся объёмами понятий A и B – значит указать объем нового понятия, элементами которого являются те и только те объекты, которые одновременно принадлежат и объему A, и объему B.

2. Объединение 
Объединить два множества, являющиеся объёмами понятий A и B – значит указать объем нового понятия, элементами которого являются те и только те объекты, которые принадлежат или объему A, или объему B.
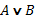
3.  Вычитание
Вычитание 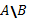
Вычесть из множества, являющиеся объёмом понятия A, понятие, множество, являющееся множеством понятия B – значит указать объем нового понятия, элементами которого являются те и только те объекты, которые принадлежат объему A, но не принадлежат объему B.

4.  Взятие дополнения
Взятие дополнения 
Взять дополнение к множеству A, значит указать объем нового понятия, элементами которого являются те и только те объекты, которые не принадлежат объему A.
˥A
1. 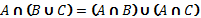
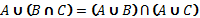
2. 
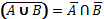
3. 
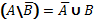
Два понятия α A (α) и α B (α) считаются сравнимыми, если и только если их универсумы совпадают. В противном случае понятия считаются несравнимыми.
3 фундаментальных отношения:
1. α A (α) и α B (α) находятся в отношении совместимости если и только если для их объемов верно, что в них имеется по крайней мере один общий элемент.
2. α B (α) находится в отношении включенного понятия α A (α) если и только если для их объемов A и B верно, что каждый элемент из B является так же элементом A.
3. Два понятия α A (α) и α B (α) находятся в отношении исчерпывания если и только если для их объемов A и B верно, что каждый элемент универсума является элементом A или элементом B.
Вспомогательные отношения.
1. Равнообъемность
1. Совместимость
2. Обоюдная включенность
3. Неисчерпывание
2.  A подчиняется B
A подчиняется B
1. Совместимость
2. A включается в B
3. Неисчерпывание
3.  B подчиняется A
B подчиняется A
1. Совместимость
2. B включается в A
3. Неисчерпывание
4.  Дополнительность
Дополнительность
1. Совместимость
2. Невключение
3. Исчерпывание
5.  Противоречие
Противоречие
1. Несовместимость
2. Невключение
3. Исчерпывание
6. 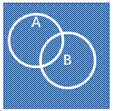 Пересечение
Пересечение
1. Совместимость
2. Невключение
3. Неисчерпывание
7. 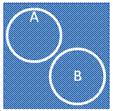 Соподчинение
Соподчинение
1. Несовместимость
2. Невключение
3. Неисчерпывание
Операции над объемами понятий
1. Обобщить непустое понятие α A (α) значит указать такое понятие α B (α), что для их объемов A и B будет верно включение первого во второе.
Предел обобщения – универсальное понятие.
2. Ограничить непустое понятие α B (α), значит указать такое непустое понятие α A (α), что для их объемов A и B будет верно включение первого во второе.
Предел ограничения – единичное понятие.
3. Под делением непустого понятия α B (α) понимают переход от объема этого понятия B к системе 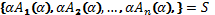
α B (α) – делимое понятие
S – система членов деления
 - член деления
- член деления
основание деления – это та характеристика элементов из объема делимого понятия, модификация которой и вызывает систему членов деления S.
Деление считается правильным если и только если оно удовлетворяет следующим условиям:
1. Каждый член деления является видовым по отношению к делимым понятиям.
2. Члены деления попарно несовместимы.
3. Объединение всех членов деления равно объему делимого понятия.
4. Каждый член деления не пуст.
5. Деление должно проводиться по одному основанию.
Виды деления:
· Дихотомическое
· По видоизменению основания
Определение
Определение – это логическая процедура придания точного смысла языковым выражениям (терминам языка).
Основная функция определения – задание значения для определяемого термина.
3 приема, сходных с определением:
1. Остенсивное «определение» (указание на предмет)
2. Описание (простое перечисление известных характеристик предмета)
3. Сравнение (одного предмета с другим)
Требования, предъявляемые к определению
1. Ясность и четкость – определение должно даваться через знакомые термины, не должно содержать лишней информации.
2. Система определений не должна содержать порочного круга (не должна замкнуться).
Виды определений: явные и неявные
· 
 Явные – задаются лингвистической конструкцией следующего вида:
Явные – задаются лингвистической конструкцией следующего вида:
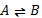

В определяемой части содержится определяемый термин.
Виды явных определений в зависимости от того, к какой языковой категории принадлежит A:
1. Определение имени
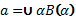 – сложное имя
– сложное имя
a – тот самый α который обладает признаком B(α)
2. 
 Определение универсалии
Определение универсалии
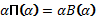
3. Определение высказывательной формы

4. Определение функционального выражения
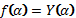
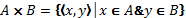
α – индивидуальная константа или индивидуальная переменная
П – предикат
f – функтор
Определяемый термин не должен содержаться в определяемой части.
Явные определения:
· Родовидовые
o Генетические – B(α) указывает на способ порождения предикатов
o Квалифицированные - B(α) указывает на существования характеристики или структурные особенности предмета
o Целевые - B(α) указывает на значение предмета
o Операциональные - B(α) указывает на процедуру, с помощью которой можно определить подпадает ли данные предмет под неявное определение
· Неродовидовые
Определения универсалий бывают перечислительными определениями.
Определение имени – определение имени через гипостазирование.
I. Обобщающая абстракция
отцовство - «x отец y»
<x, y> (мужчина x & родители (x, y))
II. Изолирующая абстракция
«быть отцом»
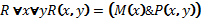
III. Гипостазирование: имя отношения «отцовство»

IV. Определение
отцовство = 
Закон


Неявные определения
Задаются лингвистической конструкцией следующего вида:
A есть то, что удовлетворяет условию 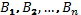
Особенности неявного определения:
1. 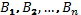 - высказывания, могут быть истинными или ложными
- высказывания, могут быть истинными или ложными
2. Определяемый термин может содержаться в определяемой части
3. Не действует принцип замены по дифиниции
Бывают:
· Индуктивные (с их помощью задаются множества)
1. Базис индукции
2, 3, 4…n индуктивные шаги
n+1 ничто иное не является A
· Рекурсивные – с их помощью задаются функции
1. Базис рекурсии
2. Рекурсия
…
x+0=x
· Аксиоматические (фундаментальные понятия)
Еще определения бывают:
· Контекстуальные – определяемая или определяющая часть содержит контекст употребления данного определения.
· Неконтекстуальные
А так же:
· Реальные
С семантической точки зрения, реальное определение – это то, которое дается действительно существующему объекту или его характеристикам
С прагматической – которое дается для уточнения смысла.
· Номинальные – выражает собой простую конвекцию называть тот или иной объект каким либо словом.
Подробнее об индукции советую прочитать в работе А. И. Ноткина «Учебник по индукции»
Учебное пособие
Дисциплина ЕН.Ф.05 ХИМИЯ.
Статус дисциплины обязательная.
Специальности (направления)). 120100, 130400, 190900, 351100, 170600, 060800, 071900, 171200, 171500, 230100.
Форма обучения всех форм обучения.
Бийск 2004
УДК 546 (075.5)
Макрушина Т.И. Химия. Учебное пособие.
Алт. гос. тех. ун-т БТИ. – Бийск.
Изд-ство Алт. гос. тех. ун-та, 2004. – 221 с.
Настоящее учебное пособие содержит основные теоретические сведения и методические рекомендации по изучению курса «Химия». Для лучшего усвоения материала студентам предложены вопросы и задания для самоконтроля.
Учебное пособие предназначено для студентов специальностей 120100 – Технология машиностроения, 130400 – Ракетные двигатели, 190900 – Информационно-измерительная техника и технологии, 351100 – Товароведение и экспертиза товаров, 170600 – Машины и аппараты пищевых производств, 060800 – Экономика и управление на предприятии, 071900 – Информационные системы и технологии, 171200 – Автоматизированное производство химических предприятий, 171500 – Высокоэнергетические устройства автоматических систем, 230100 – Эксплуатация и обслуживание транспортных технологических машин и оборудования всех форм обучения.
.
Рассмотрено и утверждено на заседании
кафедры протокол № от 2004 г
©БТИ Алт.ГТУ, 2004
Предисловие
Химия является не только общетехнической, но и общеобразовательной наукой. Поэтому инженер любой специальности должен обладать достаточными знаниями в области химии.
Изучение курса химии должно способствовать развитию у студентов логического химического мышления и диалектико-материалистического мировоззрения. В результате изучения курса студенты должны получить современное научное представление о материи и формах ее движения, о веществе как одном из видов движущейся материи, о механизме превращения химических соединений, понимать значение химии в промышленности и сельском хозяйстве. Знание курса химии необходимо для успешного изучения последующих общенаучных и специальных дисциплин. Студенты должны прочно усвоить основные законы и теории химии и овладеть техникой химических расчетов; выработать навыки самостоятельного выполнения химических экспериментов и обобщения наблюдаемых фактов.
Основной вид учебных занятий студентов-заочников — самостоятельная работа над учебным материалом. По курсу химии она слагается из следующих элементов: изучение материала по учебникам и учебным пособиям; выполнение контрольных заданий; выполнение лабораторного практикума; индивидуальные консультации (очные и письменные); посещение лекций; сдача зачета по лабораторному практикуму; сдача экзамена по всему курсу.
Работа с книгой. Изучать курс рекомендуется по темам, предварительно ознакомившись с содержанием каждой из них по программе.
Изучая курс, пользуйтесь и предметным указателем в конце книги. При первом чтении не задерживайтесь на математических выводах, составлении уравнений реакций; старайтесь получить общее представление об излагаемых вопросах, а также отмечайте трудные или неясные места. Внимательно прочитайте текст, напечатанный особым шрифтом. При повторном изучении темы усвойте все теоретические положения, математические зависимости и их выводы, а также принципы составления уравнений реакций. Вникайте в сущность того или иного вопроса, а не пытайтесь запомнить отдельные факты и явления. Изучение любого вопроса на уровне сущности, а не на уровне отдельных явлений способствует более глубокому и прочному усвоению материала. Чтобы лучше запомнить и усвоить изучаемый материал, надо обязательно иметь рабочую тетрадь и заносить в нее формулировки законов и основных понятий химии, новые незнакомые термины и названия, формулы и уравнения реакций, математические зависимости и их выводы.. Во всех случаях, когда материал поддается систематизации, составляйте графики, схемы, диаграммы, таблицы. Они очень облегчают запоминание и уменьшают объем конспектируемого материала. Пока тот или иной раздел не усвоен, переходить к изучению новых разделов не следует. Краткий конспект курса будет полезен при повторении материала в период подготовки к экзамену. Изучение курса должно обязательно сопровождаться выполнением упражнений и решением задач.
по курсу:
«Взаимозаменяемость,
|
|
|
|
Дата добавления: 2014-01-04; Просмотров: 357; Нарушение авторских прав?; Мы поможем в написании вашей работы!