Основные формулы. Момент импульса электрона (постулат Бора):

Основы квантовой механики.

Физика атома и атомного ядра.

Момент импульса электрона (постулат Бора):

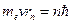
где 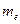– масса электрона; v – скорость электрона на 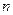–ой орбите; 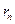радиус 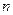–ой стационарной орбиты; 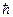– постоянная Планка; 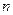– главное квантовое число (n =1,2,…).

Радиус 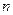–ой стационарной орбиты:

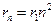
где 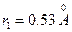– радиус Бора.

Энергия электрона в атоме водорода:

где 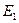=13,6 эВ –энергия ионизации атома водорода.

Энергия, излучаемая или поглощаемая атомом водорода:

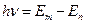
или,

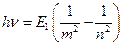
где m и n квантовые числа, соответствующие энергетическим уровням, между которыми совершаются переход электрона в атоме.

Длина волны де Бройля:

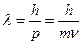
где p – импульс частицы.

Соотношение неопределённостей Гейзенберга:

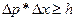(для координаты и импульса);

где 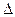р – неопределённость импульса по оси ;

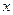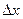– неопределённость координаты:

(для энергии и времени),

где – неопределённость энергии; 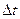– время нахождения квантовой системы в данном энергетическом состоянии.

Одномерное уравнение Шредингера для стационарных состояний:

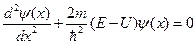
где 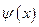– волновая функция, описывающая состояние частицы; 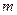– масса частицы; 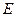– полная энергия; U – потенциальная энергия частицы.

Плотность вероятности нахождения частицы в точке с координатой x:

.

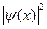Вероятность обнаружения частицы в интервале от 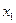до :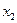

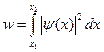
Решение уравнения Шредингера для одномерного, бесконечно глубокого, прямоугольного потенциального ящика:

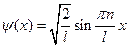
Собственные значения энергии частицы в потенциальном ящике:

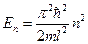
где 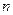– квантовое число (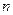=1,2,3,…); 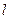– ширина ящика ().

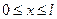Дата добавления: 2014-01-04