Определение. Соотношение неопределенностей Гэйзенберга

Соотношение неопределенностей Гэйзенберга.

Принцип неопределённости Гейзенбе́рга (или Га́йзенберга) в квантовой механике — фундаментальное неравенство (соотношение неопределённостей), устанавливающее предел точности одновременного определения пары характеризующих квантовую систему физических наблюдаемых (см. физическая величина), описываемых некоммутирующими операторами (например, координаты и импульса, тока и напряжения, электрического и магнитного поля). Соотношение неопределённостей[* 1] задаёт нижний предел для произведения среднеквадратичных отклонений пары квантовых наблюдаемых. Принцип неопределённости, открытый Вернером Гейзенбергом в 1927 г., является одним из краеугольных камней квантовой механики.

Если имеется несколько (много) идентичных копий системы в данном состоянии, то измеренные значения координаты и импульса будут подчиняться определённому распределению вероятности — это фундаментальный постулат квантовой механики. Измеряя величину среднеквадратического отклонения 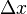координаты и среднеквадратического отклонения 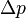импульса, мы найдем что:

,

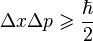где ħ — приведённая постоянная Планка.

Отметим, что это неравенство даёт несколько возможностей — состояние может быть таким, что 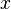может быть измерен с высокой точностью, но тогда 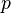будет известен только приблизительно, или наоборот 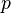может быть определён точно, в то время как 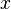— нет. Во всех же других состояниях 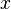и , и 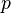могут быть измерены с «разумной» (но не произвольно высокой) точностью.

Обобщённый принцип неопределённости

Принцип неопределённости не относится только к координате и импульсу (как он был впервые предложен Гейзенбергом). В своей общей форме он применим к каждой паре сопряжённых переменных. В общем случае, и в отличие от случая координаты и импульса, обсуждённого выше, нижняя граница произведения «неопределённостей» двух сопряжённых переменных зависит от состояния системы. Принцип неопределённости становится тогда теоремой в теории операторов, которая будет приведена далее.

Теорема. Для любых самосопряжённых операторов: 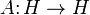и 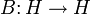, и любого элемента 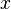из такого, что и 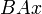оба определены (то есть, в частности, и 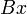также определены), имеем:

Это прямое следствие неравенства Коши — Буняковского.

Следовательно, верна следующая общая форма принципа неопределённости, впервые выведенная в 1930 г. Говардом Перси Робертсоном и (независимо) Эрвином Шрёдингером:

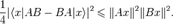
Это неравенство называют соотношением Робертсона — Шрёдингера.

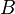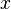Оператор называют коммутатором и и обозначают как . Он определен для тех , для которых определены оба и .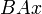

Из соотношения Робертсона — Шрёдингера немедленно следует соотношение неопределённости Гейзенберга:

Предположим, и 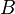— две физические величины, которые связаны с самосопряжёнными операторами. Есл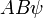и и определены, тогда:

,

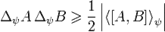где:

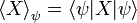
— среднее значение оператора величины в состоянии 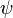системы, и

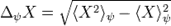
— оператор стандартного отклонения величины в состоянии 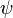системы.

Приведённые выше определения среднего и стандартного отклонения формально определены исключительно в терминах теории операторов. Утверждение становится однако более значащим, как только мы заметим, что они являются фактически средним и стандартным отклонением измеренного распределения значений. См. квантовая статистическая механика.

То же самое может быть сделано не только для пары сопряжённых операторов (например координаты и импульса, или продолжительности и энергии), но вообще для любой парыЭрмитовых операторов. Существует отношение неопределённости между напряжённостью поля и числом частиц, которое приводит к явлению виртуальных частиц.

Возможно также существование двух некоммутирующих самосопряжённых операторов и 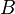, которые имеют один и тот же собственный вектор 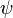. В этом случае 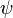представляет собой чистое состояние, которое является одновременно измеримым для и .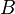

Дата добавления: 2014-01-04