Определение коэффициента поверхностного натяжения жидкости методом отрыва капель

Лабораторная работа №2

Приборы и принадлежности: установка для определения поверхностного натяжения методом отрыва капель, исследуемая жидкость, ртутный или спиртовой термометр, мензурка.

Цель работы: определение величины коэффициента поверхностного натяжения исследуемой жидкости и характер его изменения при повышении температуры.

Поверхностное натяжение жидкости – это свойство границы раздела между жидкостью и воздухом, находящимся в контакте с ее свободной поверхностью. Поверхностное натяжение обусловлено тем, что молекула жидкости на поверхности испытывает действие сил только соседних молекул, находящихся в контакте с ней, в то время как молекула внутри жидкости испытывает воздействие со всех сторон (рис. 1). Следовательно, молекула на поверхности испытывает воздействие результирующей силы, направленной ортогонально к свободной поверхности внутрь жидкости. Поэтому, для того, чтобы увеличить площадь свободной поверхности жидкости за счет переноса молекул из глубины, необходимо затратить некоторую энергию. Отношение

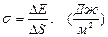, (1)

называют коэффициентом поверхностного натяжения, где 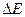- свободная энергия, 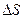- изменение площади поверхности жидкости при фиксированном значении температуры.

Поверхностная энергия измеряется работой, затраченной на создание единицы новой поверхности. Поскольку 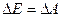, а 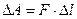, соответственно 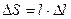, следовательно, на основании уравнения (1), можно записать:

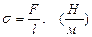, (2)

где 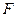- сила, 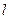- длина контура жидкой пленки.

Из выражения (2) следует, что коэффициент поверхностного натяжения представляет собой силу, действующую на единицу длины контура.

Таким образом, поверхностная энергия, приходящаяся на единицу площади численно равна действующей на единице длины силе. Эта сила и называется коэффициентом поверхностного натяжения.

С ростом температуры поверхностное натяжение уменьшается и при критической температуре обращается в нуль. Температурная зависимость 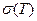определяется выражением:

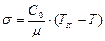, (3)

где 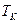- критическая температура, 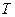- температура исследуемой жидкости, 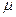- молярная масса, 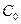- const.

Растворенные в жидкости вещества, которые понижают величину поверхностного натяжения, называются поверхностно-активными веществами (ПАВ).

В медицинской практике поверхностное натяжение используется как диагностический параметр. Известно, что в норме величина поверхностного натяжения плазмы крови и мочи человека составляет соответственно 72 и 76 дин/см. Появление в моче желчных пигментов приводит к резкому снижению коэффициента поверхностного натяжения до 56 дин/см.

Исследованию взаимодействия жидкости с твердой поверхностью уделяется достаточно много внимания, т.к. процессы смачивания и растекания, капиллярные явления весьма актуальны для многих технологических процессов и медицины. На этих явлениях основаны процессы пайки и сварки металлов и других материалов, склеивание, нанесение поверхностных слоев и т.д.

Процесс смачивания можно характеризовать так называемым краевым углом 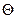или углом смачивания (рис. 2).

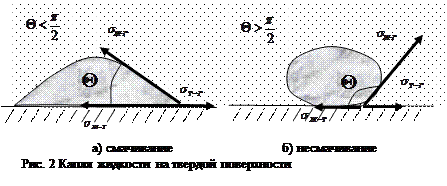
Равновесие капли на поверхности твердого тела выражается уравнением:

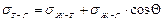, (4)

где 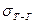- вектор поверхностного натяжения между твердым телом и газом (воздухом), 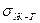- вектор поверхностного натяжения между жидкостью и газом, 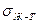- вектор поверхностного натяжения между жидкостью и твердым телом. Уравнение (4) показывает взаимосвязь параметров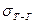, , 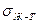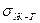и .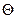

Энергия смачивания – работа создания единицы новой смоченной поверхности твердого тела:

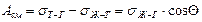(5)

Чем меньше краевой угол и больше поверхностное натяжение 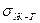, тем больше энергия смачивания.

Энергия адгезии – работа удаления жидкости с поверхности твердого тела. Она определяется (рис. 3а) заменой 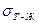на освобожденных поверхностях 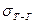и :

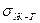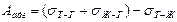. (6)

Используя уравнение (4), можно написать:

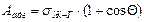. (7)

При этом сохраняются те же зависимости, что и для работы смачивания, т.е. увеличение работы адгезии при росте 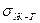и уменьшении краевого угла.

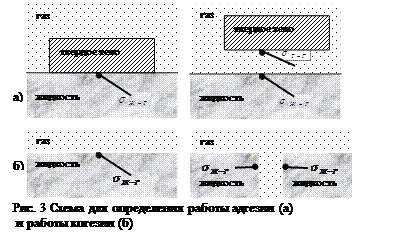Энергия когезии – работа разрыва жидкости или образования двух новых поверхностей жидкость – газ (рис. 3б). Работа когезии определяется следующим выражением:

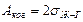. (8)

В уравнении (4) постоянной величиной является вектор 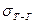, в то время как вектор 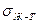и 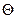могут изменяться со временем за счет возможного растворения поверхности твердого тела, а следовательно, и изменения состава жидкости.

Рассмотрим определение коэффициента поверхностного натяжения жидкости методом отрыва капли при ее медленном протекании через капилляр. Исследуемая жидкость капает из стеклянного капилляра радиусом 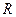, нижний конец которого тщательно отполирован. Капли падают в мензурку, помещенную под капилляром (рис. 4).

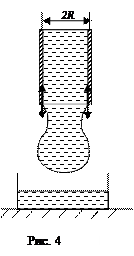Капля будет удерживаться на конце капилляра до тех пор, пока ее вес

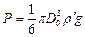, (9)

где 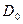- отрывной диаметр капли, 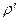- плотность жидкости, 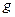- ускорение свободного падения, будет меньше силы поверхностного натяжения, действующей по нижней кромке капилляра:

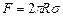. (10)

Однако, как только капля станет настолько тяжелой, что вес будет удовлетворять равенству:

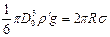, (11)

капля оторвется. Из уравнения (11) следует, что:

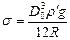. (12)

Будем считать, что оторвалось 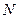капель, при этом масса 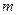одной капли будет равна: 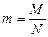, (13)

где 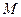- масса всей жидкости, вытекшей из капилляра.

С другой стороны, 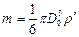, (14)

следовательно, имеет место равенство 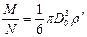, (15)

из которого следует, что 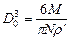. (16)

Подставив (16) в (11), получим: 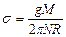. (17)

Уравнение (17) и определяет величину коэффициента поверхностного натяжения исследуемой жидкости. Учитывая, что 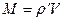(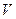- объем вытекшей жидкости), уравнение (17) можно представить в следующем виде:

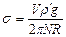, (18)

и которое можно использовать для определения коэффициента поверхностного натяжения.

Дата добавления: 2014-01-04