Изучение электростатического поля

Лабораторная работа № 21

Порядок выполнения работы

1. Получить на экране контрастную дифракционную картину с помощью дифракционной решетки с известным периодом.

2. Определить длину волны, пользуясь выражением (6). Результаты измерений и вычислений занести в таблицу 1.

Таблица 1

Порядок дифракционного максимума	х, мм	l, мм	tg j	l, нм	Dl, нм	E =(Dl /l) 100%
k = 1
k= 2
k = 3

3. По известным значениям определить неизвестный период дифракционной решетки, пользуясь выражением (7). Результаты измерений и вычислений занести в таблицу 2.

Таблица 2

Порядок дифракционного максимума	х, мм	l, мм	l, нм	d, мм	Dd, мм	E =(Dd/d) 100%
k = 1
k = 2
k = 3

4. Повторить пункты 1 — 3 с использованием ПРК-2 в качестве излучателя.

5. Рассчитать абсолютную и относительную погрешности измерений.

6. По полученным данным сделать вывод.

Контрольные вопросы

1. Что такое дифракция? 2. В чем суть зонной теории Френеля? 3. Как объяснить с точки зрения зонной теории Френеля условие возникновения дифракционного максимума и минимума? 4. Что такое лазер? 5. Где можно использовать лазер в медицинской практике? 6. В чем заключается преимущество лазерного излучения? 7. Где используются газовые горелки типа ПРК в медицине?

Приборы и принадлежности: стеклянная ванна, набор электродов, координатная сетка, источник постоянного тока, потенциометр, гальванометр, вольтметр.

Цель работы: изучение силовой и энергетической характеристик токового диполя.

Электрическое поле — частная форма проявления электромагнитного поля. Электрическое поле создается электрическими зарядами или при изменении во времени магнитного поля. Характеристикой электрического поля служит напряженность электрического поля и потенциал. Рассмотрим поле точечного заряда.

Всякий заряд (точечный в том числе) изменяет свойства окружающего его пространства — создает в нем электрическое поле. Это поле проявляет себя в том, что помещенный в какую-либо точку электрический заряд оказывается под действием силы этого поля. По величине силы, действующей на данный заряд, можно, очевидно, судить об интенсивности поля. Данный заряд называют обычно “пробный заряд”.

Исследуем с помощью точечного пробного заряда q_пр поле, создаваемое точечным зарядом q (рис. 1).

Поместив пробный заряд в точку, положение которой относительно заряда q определяется радиус-вектором r, мы обнаружим, что на пробный заряд действует сила, которая описывается законом Кулона:

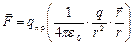(1)

Из формулы (1) следует, что сила, действующая на пробный заряд, зависит не только от величины, определяется поле (от q и r), но и от величины пробного заряда q_пр. Если брать разные по величине пробные заряды q^/_пр и q^//_пр и т.д., то и силы F^/.. F^//...., которые они испытывают в данной точке поля, будут различны. Легко, однако, видеть из формулы (1), что отношение F/q_пр для всех пробных зарядов будет одно и то же и зависит лишь от величины q и r, определяющих поле в данной точке. Поэтому это отношение можно принять в качестве величины, характеризующей электрическое поле:

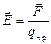. (2)

Векторную величину формулы (2) называют напряженностью электрического поля в данной точке.

К понятию напряженности электрического поля мы пришли, исследуя электрическое поле точечного заряда. Однако определение (2) распространяется и на тот случай, когда поле создается любой совокупностью зарядов.

Для описания электрического поля отдельного заряда или системы зарядов необходимо указать величину и направление вектора 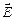для каждой точки поля.

Удобнее, однако, описывать электрическое поле с помощью линий напряженности. Линии напряженности проводятся таким образом, чтобы касательная к ним в каждой точке совпадала с направлением вектора .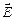

Густота линий выбирается так, чтобы количество линий, пронизывающих единицу поверхности, перпендикулярной к линиям площадки, было равно численному значению вектора 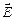. Тогда по картине линий напряженности можно судить о направлении и величине вектора 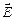в разных точках пространства.

Очевидно, что перемещение одного заряда в поле другого или других будет сопровождаться совершением работы, которая на элементарном перемещении dr может быть представлена следующим образом:

.

Работа на пути 1 — 2 определяется выражением:

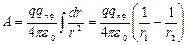, (3)

где r₁ и r₂ — радиус-векторы, проведенные в точки 1 и 2 соответственно.

Из (3) следует, что в электрическом поле работа перемещения не зависит от формы пути, а определяется только начальным и конечным положениями заряда в пространстве. Такое поле сил называется потенциальным, т.е. работа (3) может быть представлена как разность значений потенциальной энергии, которыми обладал заряд q_пр в точках 1 и 2 поля заряда q.

.

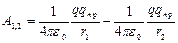Отсюда для потенциальной энергии заряда q_пр в поле заряда q получаем

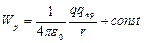. (4)

Значение const в выражении (4) выбирается таким образом, чтобы при удалении заряда на бесконечность (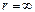) потенциальная энергия обращалась в нуль, тогда:

. (5)

Различным пробным зарядам в одной и той же точке поля будут соответствовать различные значения энергии W^/_p, W^//_p,... но, как видно из (5), отношение W_p/q_пр для всех зарядов будет одно и то же. Величина

(6)

называется потенциалом поля точечного заряда в данной точке и наряду с напряженностью поля 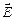используется при описании электрических полей. Действительно, работа сил поля над зарядом q на отрезке пути dl может быть представлена с одной стороны как qE_ldl (E_l — проекция вектора 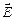на направление dl), с другой стороны, как убыль потенциальной энергии заряда, т.е. как

.

Приравнивая эти выражения, получим:

,

где через E _l обозначено произвольно выбранное направление в пространстве. В частности,

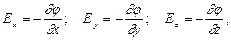
откуда

Выражение, стоящее в скобках, называется градиентом скаляра j (обозначается gradj), тогда

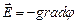. (7)

Градиент некоторой скалярной функции j (x,y,z) есть векторная величина, обладающая следующим свойством: направление градиента совпадает с направлением , в котором при смещении из данной точки функции j, возрастая по величине, изменяется с наибольшей скоростью. На этом свойстве и основан метод построения электрических полей. Построим для примера картину электрического поля для положительного точечного заряда.

Согласно соотношению (6) потенциалы точек заряда q будут различны для различных r и одинаковы во всем пространстве, окружающем заряд q, для неизменных r. Поверхность или линия, объединяющая точки одинакового потенциала, называется эквипотенциальной поверхностью или линией.

Для точечного заряда эти поверхности, очевидно, будут представляться как группа концентрических сфер с зарядом в центре.

Так как r может приобретать любые значения от 0 до , то и число эквипотенциальных поверхностей будет бесконечно, однако условились проводить их так, чтобы изменение потенциала было всюду одинаковым (рис. 2 а). Из соотношения (7) очевидно, что вектор 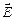для точечного положительного заряда будет совпадать с направлением радиуса r и направлен от заряда.

Таким образом, зная расположение эквипотенциальных поверхностей поля, можно легко построить линии напряженности, т.к. в любой точке эквипотенциальной поверхности (линии) согласно соотношению (7) вектор 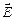совпадает с направлением нормали к поверхности (линии) в той же точке; последнее обстоятельство и используется в данной лабораторной работе для построения картины поля.

Электрические потенциалы, которые возникают в клетках, тканях и органах живого организма, называют биопотенциалами. Биопотенциалы имеют ионную природу и образуются вследствие разницы концентраций положительных и отрицательных ионов внутри и снаружи клетки. Эта разница активно поддерживается в процессе жизнедеятельности клетки. Биопотенциалы разделяют на потенциалы покоя и потенциалы действия. Потенциалы покоя имеют постоянный характер по величине разности потенциалов, устанавливающейся между внутренней средой клетки и внешней средой на поверхности мембраны клетки. При возбуждении клетки происходит изменение концентрации ионов внутри и снаружи клетки, что вызывает изменение величины и знака этих потенциалов. Эти изменения называются потенциалом действия. Они представляют импульсы постоянного или переменного знака. Суммируясь, потенциалы отдельных клеток образуют результирующую разность потенциалов ткани или органа, которая может быть измерена и зарегистрирована с помощью соответствующих приборов, например, электрокардиографа. Поскольку биопотенциалы очень точно отражают функциональное состояние органов и тканей в норме и патологии, их широко используют при физиологических исследованиях и при диагностике заболеваний. Наибольшее распространение имеют методы регистрации биопотенциалов сердца (электрокардиография — ЭКГ), головного мозга (электроэнцефалография — ЭЭГ), периферических нервных стволов и мышц (электромиография — ЭМГ) и т.д.

Электрическое поле в зависимости от вида электродов и их расположения может иметь весьма разнообразную форму. В данной работе исследуется поле токового диполя или дипольного электрического генератора, представляющего собой систему, состоящую из двух полюсов, на которые с помощью источника постоянного тока подаются и поддерживаются длительное время заряды, равные по величине и противоположные по знаку. Поле токового диполя аналогично полю диполя сердца (рис. 2 б), поэтому изучение поля дипольного электрического генератора представляет интерес для студентов-медиков.

Дата добавления: 2014-01-04