Тема 5. Твердое тело в механике

Вращательное движение – это движение, при котором все точки тела движутся по окружности, и центр окружности расположен на одной прямой, называемой осью вращения.

При вращательном движении положение тела в любой момент времени определяется углом поворота j радиуса вектора R любой точки тела относительно своего начального положения [ j ] - [ рад ].

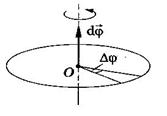
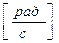Угол j - угловой путь при вращательном движении. При вращательном движении угловая скорость - w. [ w ] –

- мгновенная угловая скорость при

неравномерном движении.

- угловая скорость при равномерном

движении.

Dj = 2p - угол, соответствующий одному полному обороту тела.

Dt = T – соответствующее время или период обращения.

Если вращение тела происходит неравномерно, то быстроту изменения угловой скорости характеризуют угловым ускорением

Направление угловой скорости определяется по правилу буравчика: направление вектора угловой скорости совпадает с направлением поступательного движения буравчика, рукоятка которого вращается вместе с телом.

1) w = const, j = wt - равномерное движение

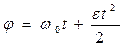2) e > 0 - равноускоренное движение

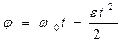3) e < 0 - равнозамедленное движение

- угловая скорость при равноускоренном движении.

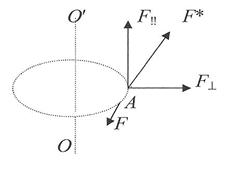
Пусть твердое тело произвольной формы вращается под действием силы F* вокруг неподвижной оси О¢О. Все его точки описывают окружности с центрами на этой оси Разложим силу F* на три состав-ляющие: F‼, F^ и F (перпендикулярную силам F‼ и F^).

Вращение тела вызывает только сила F, являющаяся касательной к окружности. Силу F – называют вращающей силой. Действие силы F зависит не только от её значения, но и от расстояния точки её приложения А до оси вращения, т.е. зависит от момента силы.

Моментом силы называется произведение вращающей силы F на радиус окружности r, описываемой точкой приложения силы

M = F×r - момент силы [ H×м ]

Моментом инерции материальной точки относительно некоторой оси, называется произведение массы материальной точки на квадрат расстояния до этой оси.

J = m×r² - момент инерции [ кг×м² ]

Момент инерции характеризует инертность тела при вращательном движении.

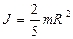Моменты инерции разных симметричных тел массой m:

- момент инерции шара с радиусом R

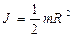- момент инерции цилиндра

- момент инерции стержня

Во всех перечисленных примерах ось вращения проходит через центр масс тела.

Момент инерции относительно любой произвольной оси, не проходящей через центр масс, определяется по теореме Штейнера:

J = J₀ + md²

Момент инерции относительно любой произвольной оси, не проходящей через центр тяжести равен сумме момента инерции относительно параллельной оси, проходящей через центр тяжести и произведению массы на квадрат расстояния между этими осями.

II закон Ньютона – основной закон динамики поступательного движения

F = ma

Умножив обе стороны уравнения на r, получим:

F×r = mar

Причем, а = e×r, Fr = M, mr² = J

Следовательно,

М = J×e - основное уравнение динамики вращательного движени я или II закон Ньютона для вращательного движения.

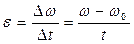Угловое ускорение

Тогда, умножив обе стороны уравнения на Dt получим следующее:

- основной закон

динамики вращательного движения.

MDt – импульс момента сил (импульс вращающегося момента).

L = Jw - момент импульса (момент количества движения).

Тогда аналогично закону сохранения импульса

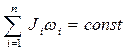- закон сохранения момента импульса

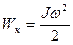При вращательном движении кинетическая энергия определяется по формуле

Катящийся без скольжения шар совершает вращательное и поступательное движения одновременно. И полная энергия равна

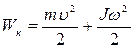W_к = W_пост + W_вращ или

Таким образом, мы выяснили, что

S,u,a, t – кинематические характеристики поступательного движения

j,w,e, t – кинематические характеристики вращательного движения

F, m, p - динамические характеристики поступательного движения

M, J, L - динамические характеристики вращательного движения

Дата добавления: 2014-01-04