
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Т е о р и я м е т о д а. 1. Установить грузы m1 на расстоянии R 1
|
|
|
|
ЖИДКОСТИ МЕТОДОМ СТОКСА
ОПРЕДЕЛЕНИЕ КОЭФФИЦИЕНТА ВЯЗКОСТИ
П о р я д о к р а б о т ы
1. Установить грузы m1 на расстоянии R 1.
2. Установить маятник так, чтобы черта на мишени показывала угол нуль градусов (j = 0).
3. Выстрелить из стреляющего устройства и замерить угол отклонения маятника j0, остановить маятник рукой.
4. Включить сетевой шнур и нажать клавишу СЕТЬ, на лицевой стороне миллисекундомера высвечиваются нули.
5. Рукой отклонить маятник на угол, полученный при выстреле снаряда и замерить время t1 десяти колебаний n = 10. Вычислить период колебаний.
6. Передвинуть грузы m 1 на расстояние R2 и, нажав клавишу CБРОС повторить пункт 5. Вычислить период колебаний.
7. Все измерения занести в таблицу и вычислить скорость u полета
снаряда.
Таблица
Контрольные вопросы
1. Почему маятник называется крутильно-баллистическим?
2. Из чего состоит маятник и для чего на маятник насажены два груза массой m1 ?
3. Какой закон используется для нахождения скорости полета снаряда?
4. Как определяется в работе угловая скорость?
2. Как определяется момент инерции маятника в данной работе?
Л а б о р а т о р н а я р а б о т а № 14
Ц е л ь р а б о т ы: изучение законов движения тел в вязкой среде.
П р и б о р ы: стеклянный цилиндр с жидкостью на подставке, секундомер, микрометр, шарики.
При движении жидкости или газа возникают силы внутреннего трения. Эти силы возникают вследствие того, что движение жидкости или газа слоистое и скорости перемещения слоев разные. Силы внутреннего трения направлены к уравниванию скорости движения всех слоев. Уравнивание скорости слоев осуществляется путем передачи импульса молекулами более быстрого слоя молекулам слоя, движущегося медленно. Это приводит к увеличению скорости движения более медленного слоя. Слой же, движущийся быстрее, начинает двигаться медленнее, так как молекулы из медленного слоя, попадая в более быстрой слой, получают в быстром слое импульс, что приводит к его торможению. Таким образом, внутреннее трение обусловлено переносом импульса m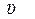 молекулами вещества, которые переходят из слоя в слой и создают силы трения между слоями газа или жидкости перемещающимися с различными скоростями. Опыт показал, что сила внутреннего трения F пропорциональна градиенту скорости
молекулами вещества, которые переходят из слоя в слой и создают силы трения между слоями газа или жидкости перемещающимися с различными скоростями. Опыт показал, что сила внутреннего трения F пропорциональна градиенту скорости  и площади соприкасающихся слоев
и площади соприкасающихся слоев 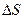 . Коэффициент пропорциональности h называется коэффициентом вязкости.
. Коэффициент пропорциональности h называется коэффициентом вязкости.
F = - h 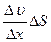 (1)
(1)
    υ1 υ1
| Знак «-» в формуле показывает, что сила F направлена противоположно вектору скорости. Градиентом скорости называется изменение скорости на единицу длины 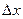 в направлении, перпендикулярном скорости движения слоев. в направлении, перпендикулярном скорости движения слоев.
|
Коэффициент динамической вязкости или внутреннего трения, есть физическая величина, численно равная силе внутреннего трения, между слоями с площадью, равной единице, при градиенте скорости, равном единице h = 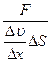 (2)
(2)
Размерность коэффициента вязкости в СИ [ h ] = [ ]
]
Наряду с коэффициентом динамической вязкости часто употребляют коэффициент кинематической вязкости
ν = 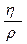 где ρ - плотность жидкости
где ρ - плотность жидкости
Коэффициент вязкости может быть определен методом падающего груза в вязкой среде (метод Стокса). Рассмотрим свободное падение шарика в вязкой покоящейся жидкости (рис.) На шарик действуют
I. Сила тяжести Р= mg= 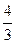 pr3rg (3)
pr3rg (3)
где r – радиус шарика, r - плотность шарика, q - ускорение свободного падения.
2. Выталкивающая сила (по закону Архимеда)
FA = m1g = 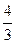 pr3r1g (4)
pr3r1g (4)
где r1 – плотность жидкости.
3. Сила сопротивления движению, вычисленная Стоксом, обусловленная силами внутреннего трения между слоями жидкости
FC = 6 p h ru (5)
где u - скорость слоев жидкости.
Здесь играет роль не трение шарика о жидкость, а трение отдельных слоев жидкости друг о друга, т.к. при прикосновении твердого тела с жидкостью к поверхности тела тотчас же прилипают молекулы жидкости. Тело обволакивается слоями жидкости и связано с ними межмолекулярными силами. Непосредственно прилегающий к телу слой жидкости движется вместе с телом со скоростью движения тела. Этот слой увлекает в своем движении соседние слои жидкости, которые на некоторый период времени приходят в плавное безвихревое движение (если малые скорости и маленькие шарики). Равнодействующая сил, действующих на шарик R = P – (FA+FC) (6)
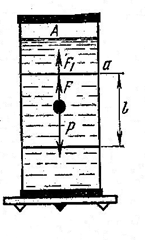
| Вначале скорость движения шарика будет воз-растать, но так как по мере увеличения скорости шарика сила сопротивления будет также возрас-тать, но наступит такой момент, когда сила тяжести Р будет уровновешана суммой сил FA и FC, т.е.
R = 0; P = FA + FC (7)
C этого момента движение шарика становится равномерным с какой-то скоростью u 0. Подставляя в формулу (7) соответствующие значения Р, FA и FC получим для коэффициента вязкости выражение
h = 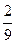 (r -r1) (r -r1)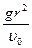 (8) (8)
|
Экспериментальная установка состоит из стеклянного цилиндра наполненного жидкостью. На цилиндр нанесены две горизонтальные метки, расположенные друг от друга на расстоянии 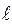 . Диаметры шариков измеряют микрометром.
. Диаметры шариков измеряют микрометром.
|
|
|
|
|
Дата добавления: 2014-01-04; Просмотров: 299; Нарушение авторских прав?; Мы поможем в написании вашей работы!

 Δx
Δx


 υ2
υ2 Δυ
Δυ