Тема 1. Магнитное поле в вакууме

Основные свойства магнитного поля:

- магнитное поле порождается током (движущимися зарядами);

- магнитное поле обнаруживается по действию на ток.

Важная особенность магнитного поля: оно действует только на движущиеся в этом поле электрические заряды. А электрическое поле действует как на неподвижные, так и движущиеся в нем электрические заряды.

Магнитное поле характеризуется двумя величинами: вектор магнитной индукции и вектор напряженности.

Вектор магнитной индукции, В характеризует результирующее магнитное поле, создаваемое всеми макро- и микротоками, т.е. в различных средах вектор магнитной вектор В будет иметь разные значения.

Вектор напряженности Н характеризует магнитное поле макротоков.

[ B ] = [ Тл ]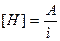

Вектор магнитной индукции В связан с вектором напряженности Н соотношением: В = mm₀Н

m₀ = 4p×10^-7 Гн/м – магнитная постоянная;

m - магнитная проницаемость среды, показывающая во сколько раз магнитное поле макротоков вектора напряженности, усиливается за счет поля микротоков среды.

Макротоки – токи, текущие в проводах, микротоки – токи, обусловленные движением электронов в атомах и молекулах. Эти микротоки создают свое магнитное поле и могут поворачиваться в магнитных полях макротоков.

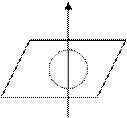Так, как магнитное поле является силовым, то его по аналогии с электрическим полем изображают с помощью линий магнитной индукции. Линиями магнитной индукции называются кривые, касательные к которым в каждой точке совпадают, с направлением вектора В. Линии магнитной индукции всегда замкнуты.

I Направление силовой линии определяется

правилом буравчика: если рукоятку бурав-

чика ввинчивать по направлению тока, то

A направление вращения ручки буравчика

указывает направление вектора магнитной

индукции.

Закон Био-Савара-Лапласа для проводника с током I, элемент dl которого создает в некоторой точке А напряженность dН имеет вид

Для магнитных полей также соблюдается принцип суперпозиции:

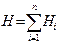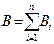Рассмотрим применение закона Био-Савара-Лапласа к расчету магнитных полей:

1.Напряженность магнитного поля для бесконечного прямолинейного проводника с током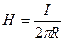

2. Напряженность магнитного поля для проводника с конечной длиной

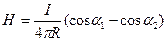
3. Напряженность магнитного поля в центре кругового тока

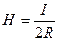
4. Напряженность магнитного поля на оси кругового тока

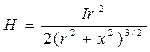где х – расстояние от произвольной точки, лежащей на оси кругового тока.

На проводник с током со стороны магнитного поля действует сила Ампера

F_A = IBl sina - сила Ампера

где a - угол между длиной проводника и вектором магнитной индукции.

Направление вектора силы Ампера определяется по правилу левой руки: если ладонь левой руки расположить так, чтобы в нее входил вектор магнитной индукции В, а четыре вытянутых пальца расположить по направлению тока в проводнике, то отогнутый большой палец покажет направление силы, действующий на ток.

Закон Ампера применяется для определения силы взаимодействия двух параллельных токов.

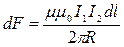- закон Ампера

Если токи имеют противоположные направления – отталкиваются, одинаковые направления - притягиваются.

Тема 2. Действие магнитного поля на токи и заряды

Поток вектора магнитной индукции (магнитный поток) через площадь dS, перпендикулярную полю, численно равен числу силовых линий, пронизывающих эту площадь

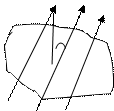
B Ф = ВScosa - магнитный поток [ Вб ]

S Поток вектора магнитной индукции Ф через

S произвольную поверхность S равна

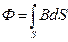
Для однородного поля и плоской поверхности, расположенных перпендикулярно вектору магнитной индукции

Ф = ВS

Если поверхность замкнута, то полный поток вектора магнитной индукции

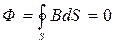- теорема Остроградского-Гаусса для магнитного поля

Эта теорема отражает факт отсутствия магнитных зарядов, вследствие чего линии магнитной индукции не имеют ни начала, ни конца и являются замкнутыми.

Выясним, как ведет себя контур с током в магнитном поле. Пусть контур малых размеров со сторонами а и ℓ по которому течет ток I.

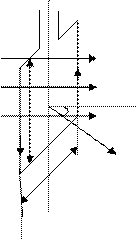0

+ - На параллельные полю стороны ℓ поле не

действует. На стороны а в соответствии

I с правилом левой руки и формулой Ампе-

B ра действует пара сил, момент которой ра-

j вен M = Fh

а где F = IBa sinb - сила Ампера

I р_m b - угол между магнитной индукцией и на-

ℓ правлением тока

0^’ h – плечо силы h = ℓcosj

0¢ j - угол между В и стороной ℓ.

Так, как sinb = 1, сторона а перпенди-

кулярна магнитной индукции В, то

F М = IBaℓcosj

ℓ aℓ = S – площадь прямоугольного контура

a B Тогда М = IBScosj

IS = р_m - магнитный момент, то

h р_m М = р_m Bcosj

F

Направление вектора р_m совпадает с положительным направлением нормали к плоскости контура, которое определяется правилом правого винта: если рукоятка винта вращается по направлению тока в контуре, то поступательное движение винта показывает направление вектора р_m.

В случае контура произвольной формы в формулу вводится угол a между векторами магнитного момента P_m и магнитной индукции В.

cosj = sin(90-j) = sina и тогда M = p_mBsina

a - угол между векторами магнитного момента р_m и магнитной индукции В.

Определим работу по перемещению проводника с током в магнитном поле. На проводник с током в магнитном поле действует сила Ампера

F = IBℓ sina

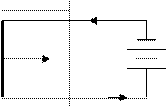
dx I Так, как поле перпендикулярно проте-

+ кающему по проводнику току, то

ℓ F a = 1 и F = IBℓ

Работа по перемещению проводника

1 2 I - dA = Fdx = IBℓ dx

ℓ dx = dS – площадь магнитного поля вектора магнитной индукции В,

которую пересек при своем движении отрезок проводника.

Тогда

dA = IB dS

B dS = dФ – поток магнитной индукции сквозь площадь dS.

Таким образом, dA = I dФ

т.е. работа по перемещению проводника с током в магнитном поле равна произведению силы тока на изменение потока магнитной индукции сквозь площадь, обтекаемую потоком.

Магнитное поле действует не только на проводник с током, но и на отдельные заряды, движущиеся в магнитном поле. Сила, действующая на заряд q, движущийся в магнитном поле со скоростью υ называется силой Лоренца.

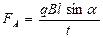
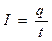Мы знаем, что сила, действующая на проводник с током F = IBlsina

Известно, что, то где ℓ - путь частиц

Тогда F_л = qυBsina - сила Лоренца

Направление силы Лоренца определяется с помощью по правилу левой руки, подразумевая, под направлением тока I направление скорости u и учитывая, что для q>0 (I и u совпадают), а для q<0 (I и u противоположны).

Направления силы F, скорости υ, и магнитной индукции В взаимно перпендикулярны. Сила Лоренца изменяет только направление скорости движения, частицы не изменяя модуля скорости. Следовательно, работа лоренцевой силы равна нулю, т.е. постоянное магнитное поле не совершает работы над движущейся в нем заряженной частицы (не изменяет кинетической энергии частицы). Переменное магнитное поле изменяет энергию и модуль скорости частицы.

Выражение для силы Лоренца позволяет найти ряд закономерностей движения заряженных частиц в магнитном поле.

1) a= 0, то есть υ ║ В, тогда сила Лоренца F_л = 0, т.е. магнитное поле на частицу не действует и она движется прямолинейно и равномерно.

2) a= 90⁰, то есть υ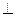 В, тогда F_л = qυB постоянна по модулю и нормальна к траектории частицы.

Согласно II – закона Ньютона, эта сила создает центростремительное ускорение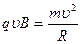

Отсюда следует, что частица будет двигаться по окружности радиусом

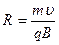
Период вращения частицы, т.е. время, затрачиваемое на один полный оборот

Вместо R подставим значение и получим

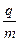– удельный заряд.

3) 0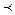 a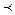 90⁰ - частица движется по винтовой линии (спирали), ось которой параллельна магнитному полю. Шаг винтовой линии

h = υ _║ T = υTcosa

Подставив вместо Т его значение, получим

h =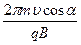

Если на движущийся заряд помимо магнитного поля действует и электрическое поле, то результирующая сила F, приложенная к заряду

F = qE + qυB – формула Лоренца

Эффект Холла – это возникновение в металле или полупроводнике с током плотностью j, помещенном в магнитном поле вектора магнитной индукции В электрического поля в направлении, перпендикулярном вектору магнитной индукции В и плотностью тока j.

Металлическую пластину с током

d 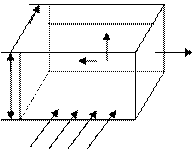- - - - - - плотностью j поместим в магнитное

F_л j поле, где вектор магнитной индукции

υ 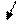перпендикулярен плотности тока.

a При данном направлении скорость

+ + + + электронов направлена в обратную

сторону.

В

На электроны действует сила Лоренца, которая направлена вверх. Тогда у верхнего края будет избыток электронов (зарядится отрицательно), а у нижнего края – их недостаток (зарядится положительно). В результате этого между пластинами возникает дополнительное поперечное электрическое поле, направленное снизу вверх. Когда напряженность Е_В этого поперечного поля достигнет такой величины, что его действие на заряды будет уравновешивать силу Лоренца, то установится стационарное распределение зарядов.

F = eE_B - электрическая сила F = eυB - сила Лоренца

Тогда eE_B = eυB

Известно, что 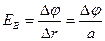, тогда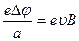

или Dj = υB a – холловская разность потенциалов

Учитывая, что I =jS = neυS Þ 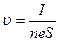получим

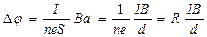где S = ad – площадь поперечного сечения,

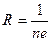- постоянная Холла, зависит от вещества

Следовательно 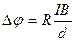- холловская разность потенциалов.

Дата добавления: 2014-01-04