Порядок декодирования

Порядок кодирования

Кодовое слово КС получается путем умножения матрицы информационной последовательности ||Х|| на образующую матрицу ||ОМ||:

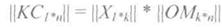
Умножение выполняется по правилам матричного умножения: (ТАК наТАК)

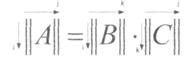
Надо только помнить, что сложение здесь ведется по модулю 2.

Пример:

допустим, образующая матрица

1000 110

0100 111

||ОМ||= 0010 011

0001 101

и вектор-строка информационной последовательности

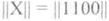
Так как множимая матрица имеет всего одну строку, умножение упрощается. В этом случае следует поставить в соответствие строкам образующей(порождающей) матрицы ||ОМ|| разряды матрицы информационной последовательности ||X|| и сложить те строки образующей(порождающей) матрицы, которые соответствуют единичным разрядам матрицы ||Х||.

Заметим, что ||KC|| = ||X, ДР||,

где ||X||- информационная последовательность (т.к. умножается на единичную матрицу ||I||),

а ||ДР|| - добавочные разряды, зависящие от матрицы добавочных разрядов ||МДР||:

|| ДР ||= || Х || * || МДР||

В результате передачи кодового слова через канал оно может быть искажено помехой. Это приведет к тому, что принятое кодовое слово ||ПКС|| может не совпасть с исходным ||КС||.

Искажение можно описать с помощью следующей формулы:

|| ПКС || = ||КС || + ||ВО ||,

где ||ВО|| - вектор ошибки - матрица-строка размерностью 1*n, с 1 в тех позициях, в которых произошли искажения.

Декодирование основано на нахождении так называемого опознавателя или синдрома ошибки -матрицы-строки ||ОП|| длиной r разрядов (r - количество добавочных или избыточных разрядов в кодовом слове).

Опознаватель используется для нахождения предполагаемого вектора ошибки.

Опознаватель находят по следующей формуле:

||ОП|| = ||ПКС||* ||ТПМ||,

где ||ПКС||- принятое и, возможно, искаженное кодовое слово;

||ТПМ||,- транспонированная проверочная матрица, которая получается из матрицы добавочных разрядов ||МДР|| путем приписывания к ней снизу единичной матрицы:

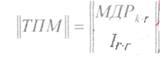
Пример ||ТПМ||:

Поскольку ||ПКС|| = ||КС|| + ||BO||, последнюю формулу можно записать в виде:

||ОП|| = ||КС|| * ||ТПМ||+||ВО|| * ||ТПМ||.

Рассмотрим первое слагаемое.

||КC|| - матрица-строка, причем первые k разрядов - информационные.

Докажем теперь, что произведение кодового слова ||КС|| на ||ТПМ|| приводит к получению нулевой матрицы ||0||.

Поскольку ||КС|| - матрица-строка, возможен упрощенный порядок умножения матриц, рассмотренных выше.

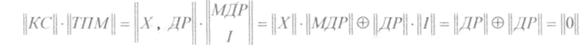
Следовательно, первое слагаемое в

||ОП|| = ||КС|| * ||ТПМ|| + ||ВО|| * ||ТПМ||

всегда равно нулю и опознаватель полностью зависит от вектора ошибки ||ВО||.

Если теперь подобрать такую проверочную матрицу ТПМ, а значит и МДР, чтобы разным векторам ошибки соответствовали разные опознаватели ОП, то по этим опознавателям можно будет находить вектор ошибки ВО, а значит и исправлять эти ошибки.

Соответствие опознавателей векторам ошибки находится заранее путем перемножения векторов исправляемых ошибок на ТПМ;

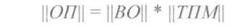
Таким ооразом, способность кода исправлять ошибки целиком определяется ||МДР||. Для построения МДР для кодов, исправляющих однократные ошибки нужно в каждой строке МДР иметь не менее 2-х единиц. При этом также необходимо иметь хотя бы одно различие между двумя любыми строчками МДР.

Полученный нами код неудобен тем, что опознаватель, хотя и связан однозначно с номером искаженного разряда, как число не равен ему. Для поиска искаженного разряда нужно использовать дополнительную таблицу соответствия между опознавателем и этим номером. Коды, в которых опознаватель как число определяет позицию искаженного разряда, были найдены и получили название кодов Хэмминга.

Построение МДР для случая исправления многократных ошибок значительно усложняется. Разными авторами были найдены различные алгоритмы построения ||МДР || для этого случая, а соответствующие коды называются именами их авторов.

Дата добавления: 2013-12-11