Графический (геометрический) метод решения задач ЛП

Свойства задач ЛП

Теорема 5.2. Множество всех допустимых решений системы ограничений задачи ЛП является выпуклым многогранником.

Теорема 5.3. Если задача линейного программирования имеет оптимальное решение, то линейная функция принимает оптимальное (максимальное или минимальное) значение в одной из угловых точек многогранника решений. Если линейная функция принимает оптимальное значение более чем в одной угловой точке, то она принимает его в любой точке, являющейся выпуклой линейной комбинацией данных угловых точек.

Точка Х называется выпуклой линейной комбинацией точек X₁, X₂, …, X_n, если выполняются условия:

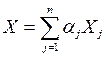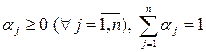, (5.14)

Теорема 5.4. Каждому допустимому базисному решению задачи линейного программирования соответствует угловая точка многогранника решений и, наоборот, каждой угловой точке многогранника решений соответствует базисное решение.

Любые m переменных системы ограничений ЗЛП (5.6), состоящей из m линейно независимых уравнений с n переменными (m < n), называются основными (или базисными), если определитель матрицы коэффициентов при них отличен от нуля. Тогда остальные n – m переменных называются неосновными (или свободными).

Базисным называют решение ЗЛП, при котором все свободные переменные равны нулю.

Пример 5.1. Решить следующую задачу линейного программирования геометрическим методом:

.

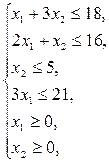
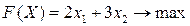Решение:

Задача линейного программирования задана в стандартной форме и имеет два проектных параметра, следовательно, возможно ее решение геометрическим методом.

1 этап: построение прямых, ограничивающих область допустимых решений (ОДР).

Рассмотрим систему ограничений задачи линейного программирования (для удобства пронумеруем неравенства):

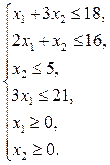
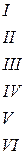
Рассмотрим первое ограничение, заменим знак неравенства знаком равенства и выразим переменную х₂ через х₁:

.

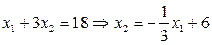Для построения прямой по данному уравнению зададим две произвольные точки, к примеру:

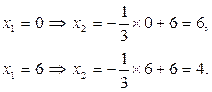
Аналогично определяем точки для остальных ограничений системы и строим по ним прямые, соответствующие каждому неравенству (рис. 5.1). Прямые пронумеруем согласно принятой ранее схеме.

2 этап: определение решения каждого из неравенств системы ограничений.

Определим полуплоскости – решения каждого из неравенств.

Рассмотрим первое неравенство системы ограничений задачи. Возьмем какую-либо точку (контрольную точку), не принадлежащую соответствующей данному неравенству прямой, например, точку (0; 0). Подставим ее в рассматриваемое неравенство:

.

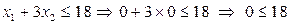При подстановке координат контрольной точки неравенство остается справедливым. Следовательно, множество точек, принадлежащих данной прямой (т.к. неравенство не строгое), а также расположенных ниже ее, будут являться решениями рассматриваемого неравенства (пометим на графике (рис. 5.1) найденную полуплоскость двумя стрелками направленными вниз рядом с прямой I)[1].

Аналогично определяем решения других неравенств и соответственно помечаем их графике. В результате график примет следующий вид:

3 этап: определение ОДР задачи линейного программирования.

Найденные полуплоскости (решения каждого из неравенств системы ограничений) при пересечении образуют многоугольник ABCDEO, который и является ОДР рассматриваемой задачи.

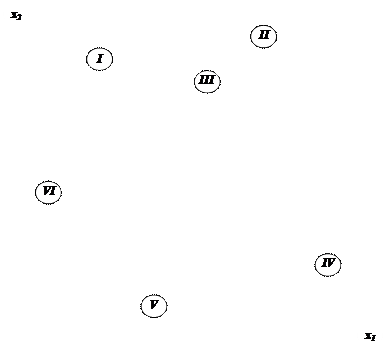
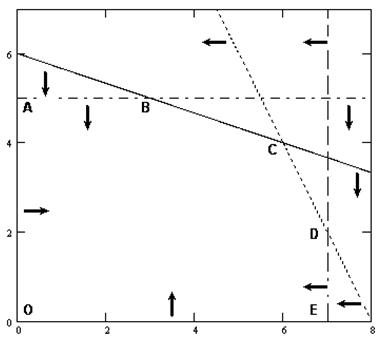
Рис. 5.1. Область допустимых решений задачи

4 этап: построение вектора-градиента.

Вектор-градиент показывает направление максимизации целевой функции[2]. Определим его координаты: координаты начальной его точки (точки приложения) – (0; 0), координаты второй точки:

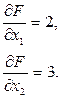
Построим данный вектор на графике (рис. 5.2).

5 этап: построение прямой целевой функции.

Рассмотрим целевую функцию данной задачи:

.

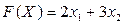Зададим ей какое-либо значение, к примеру, 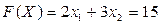. Выразим переменную х₂ через х₁:

.

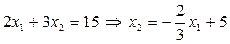Для построения прямой по данному уравнению зададим две произвольные точки, к примеру:

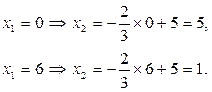
Построим прямую соответствующую целевой функции (рис. 5.2).

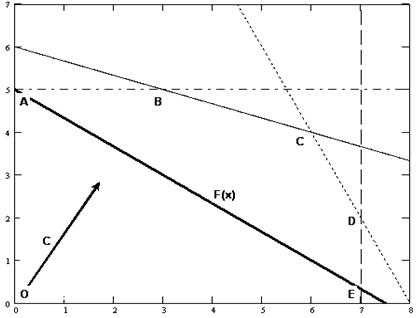
Рис. 5.2. Построение целевой функции F(X) и вектора-градиента С

6 этап: определение максимума целевой функции.

Перемещая прямую F(X) параллельно самой себе по направлению вектора-градиента, определяем крайнюю точку (точки) ОДР. Согласно графику (рис. 5.3), такой точкой является точка С ­– точка пересечения прямых I и II.

Рис. 5.3. Определение точки максимума целевой функции F(X)

Определим координаты точки С, с этой целью, решим следующую систему линейных уравнений:

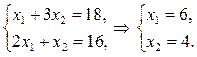
Подставим найденные координаты в целевую функцию и найдем ее оптимальное (максимальное) значение:

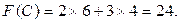
Ответ: при заданных ограничениях максимальное значение целевой функции F (Х)=24, которое достигается в точке С, координаты которой х₁ =6, х₂ =4.

Пример 5.2. Решить задачу линейного программирования геометрическим методом:

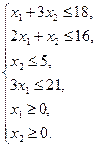
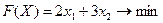
Решение:

Этапы 1-3 аналогичны соответствующим этапам предыдущей задачи.

4 этап: построение вектора-градиента.

Построение вектора-градиента осуществляется аналогично, как и в предыдущей задаче. Построим данный вектор на графике (рис. 5.4). Отметим также на данном графике стрелкой направление, обратное вектору-градиенту, – направление минимизации целевой функции F (X).

5 этап: построение прямой целевой функции.

Построение прямой целевой функции F (X) осуществляется аналогично, как и в предыдущей задаче (результат построения приведен на рис. 5.4).

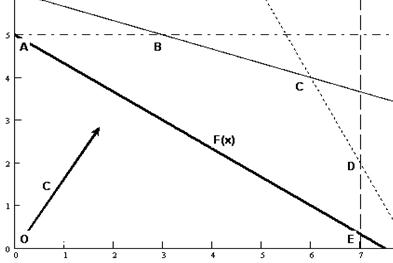
Рис. 5.4. Построение целевой функции F(x) и вектора-градиента С

6 этап: определение оптимума целевой функции.

Перемещая прямую F(x) параллельно самой себе в направлении, обратном вектору-градиенту, определяем крайнюю точку (точки) ОДР. Согласно графику (рис. 5.5), такой точкой является точка О с координатами (0; 0).

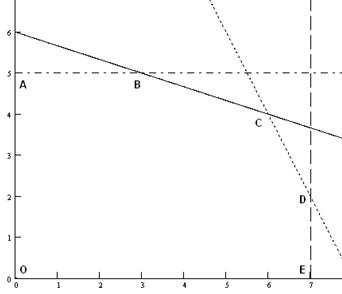
Рис. 5.5. Определение точки минимума целевой функции

Подставляя координаты точки минимума в целевую функцию, определяем ее оптимальное (минимальное) значение, которое равно 0.

Ответ: при заданных ограничениях минимальное значение целевой функции F (Х)=0, которое достигается в точке О (0; 0).

Пример 5.3. Решить следующую задачу линейного программирования геометрическим методом:

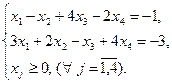
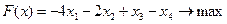
Решение:

Рассматриваемая задача линейного программирования задана в канонической форме, выделим в качестве базисных переменные x₁ и x₂.

Составим расширенную матрицу и выделим с помощью метода Жордана-Гаусса базисные переменные x₁ и x₂.

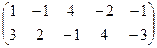
Умножим (поэлементно) первую строку на –3 и сложим со второй:

.

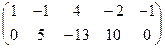Умножим вторую строку на :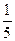

.

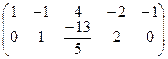Сложим вторую с первой строкой:

.

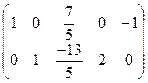В результате система ограничений примет следующий вид:

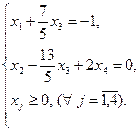
Выразим базисные переменные через свободные:

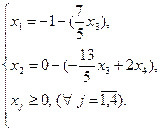
Выразим целевую функцию также через свободные переменные, для этого подставим полученные значения базисных переменных в целевую функцию:

.

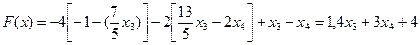Запишем полученную задачу линейного программирования

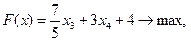
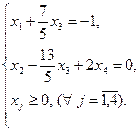
Так как переменные x₁ и x₂ неотрицательные, то полученную систему ограничений можно записать в следующем виде:

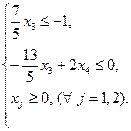
Тогда исходную задачу можно записать в виде следующей эквивалентной ей стандартной задаче линейного программирования:

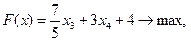
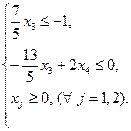
Данная задача имеет два проектных параметра, следовательно, возможно ее решение геометрическим методом.

1 этап: построение прямых, ограничивающих область допустимых решений (ОДР).

Рассмотрим систему ограничений задачи линейного программирования (для удобства пронумеруем неравенства):

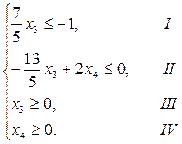
Построим прямые, соответствующие каждому неравенству (рис. 5.6). Прямые пронумеруем согласно принятой ранее схеме.

2 этап: определение решения каждого из неравенств системы ограничений.

С помощью контрольных точек определим полуплоскости – решения каждого из неравенств, и пометим их на графике (рис. 5.6) с помощью стрелок.

3 этап: определение ОДР задачи линейного программирования.

Найденные полуплоскости (решения каждого из неравенств системы ограничений) не имеют общего пересечения (так решения неравенства I противоречат в целом остальным неравенствам системы ограничений), следовательно, система ограничений не совместна и задача линейного программирования в силу этого не имеет решения.

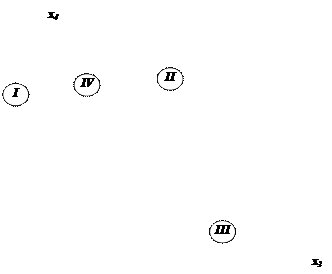
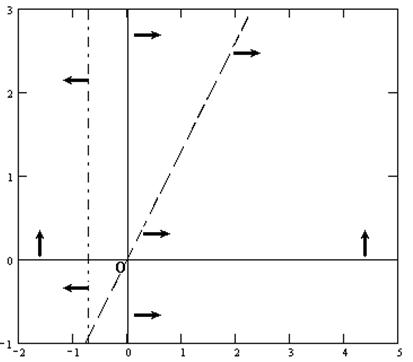
Рис. 5.6. Фрагмент MathCAD-документа:

построение области допустимых решений задачи

Ответ: рассматриваемая задача линейного программирования не имеет решения в силу несовместности системы ограничений.

Дата добавления: 2013-12-12