Соответствие переменных двойственной пары. Симплекс-таблица оптимального решения исходной задачи

Таблица 5.15

Симплекс-таблица оптимального решения исходной задачи

Таблица 5.14

СП БП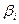
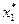
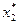
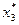
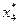
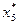
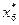
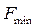
		–2	–3

В соответствии с теоремой 5.6, оптимальные значения переменных 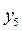и 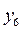будут равны абсолютным значениям коэффициентов при соответствующих переменных целевой функции исходной задачи, выраженной через свободные переменные ее оптимального решения.

По таблице 5.14 выпишем целевую функцию исходной задачи, выраженную через свободные переменные ее оптимального решения:

.

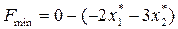Следовательно, , .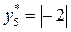

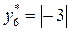Переменные 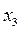, , 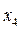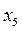и 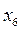не присутствуют в целевой функции (т.е. коэффициенты при них равны нулю), следовательно, оптимальные значения соответствующих им переменных 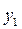, , 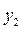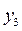и 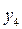равны нулю.

В соответствии с теоремой 5.5, .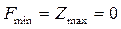

Таким образом, оптимальное значение целевой функции 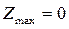, которое достигается при .

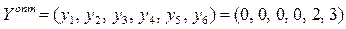Пример 5.9. На основе задачи 5.6. найдем решение двойственной задачи.

Исходная задача	Двойственная задача

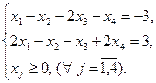
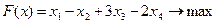
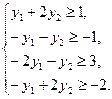
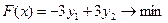
Данная двойственная пара является несимметричной. Приведем к каноническому виду двойственную задачу.

Исходная задача	Двойственная задача

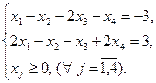
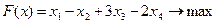
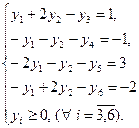
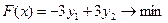
Для установления соответствия переменных двойственной пары введем в исходную задачу две недостающие фиктивные переменные.

Исходная задача	Двойственная задача

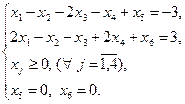
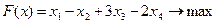
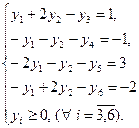
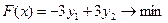
Установим соответствие между переменными взаимно двойственных задач.

Исходная задача
Основные переменные	Дополнительные переменные
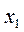
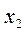
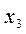
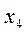
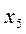
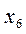
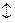
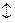
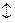
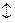
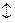
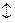
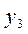
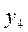
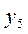
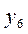
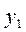
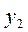
Дополнительные переменные	Основные переменные
Двойственная задача

Решим исходную задачу симплекс-методом.

Используя метод Жордана-Гаусса, выделим в системе ограничений исходной задачи в качестве базисных переменные 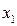и 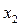(примечание: не использовать в качестве базисных фиктивные переменные).

В результате преобразований получим следующую матрицу коэффициентов:

.

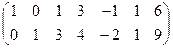Система ограничений исходной задачи примет следующий вид:

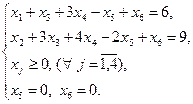
Выразим базисные переменные через свободные, в результате исходная задача примет следующий вид:

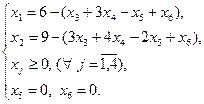
Подставив полученные значения базисных переменных в целевую функцию, она примет следующий вид:

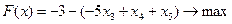
В результате решения симплекс-методом преобразованной исходной задачи на последней итерации получим следующую симплекс-таблицу:

Дата добавления: 2013-12-12