Метод потенциалов

Таблица поставок

Таблица 6.1

Задачи ЛП транспортного типа

Задачи линейного программирования транспортного типа образуют широкий круг задач, общим для которых является, как правило, распределение ресурсов, находящихся у m производителей (поставщиков), по n потребителям этих ресурсов.

Классическая транспортная задача имеет следующий вид.

Имеются m пунктов (складов) отправления груза (некоторого однородного ресурса), запасы в каждом из которых составляют соответственно a₁, a₂, …, a_m. Известна потребность в грузах b₁, b₂, …, b_n по каждому из n пунктов назначения (потребителей).

Задана матрица стоимостей доставки по каждому варианту (паре склад-поставщик – потребитель): 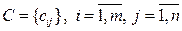, где 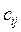– себестоимость перевозки единицы груза от i -го склада-поставщика до j -го потребителя.

Необходимо построить оптимальный план перевозок, т.е. определить, сколько груза должно быть отправлено из каждого i -го склада-поставщика каждому j -му потребителю с учетом минимизации транспортных затрат.

Пусть x_ij (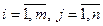) – искомый объем транспортируемого груза от i -го склада-поставщика j -му потребителю.

Исходные данные по задаче удобно представлять в виде следующей таблицы, которую называют таблицей поставок или транспортной таблицей.

Потребители Поставщики	B1	B2	…	Bn	Запасы поставщиков
A1	c11 x11	c12 x12	…	c1n x1n	a1
A2	c21 x21	c22 x22	…	c2n x2n	a2
			…
Am	cm1 xm1	cm2 xm2	…	cmn xmn	am
Потребности потребителей	b1	b2	…	bn

Задача линейного программирования транспортного типа называется закрытой, если суммарные запасы поставщиков равны суммарной потребности потребителей, т.е.

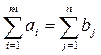. (6.2)

Если такое равенство не соблюдается, то задача является открытой.

Для того чтобы потребности всех потребителей были удовлетворены, необходимо выполнение следующей системы условий:

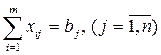. (6.3)

Аналогично, для того чтобы были задействованы все запасы складов-поставщиков, необходимо выполнение следующей системы условий:

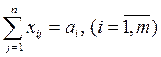. (6.4)

По своей сущности искомые переменные не могут быть отрицательными величинами, т.е.

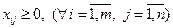(6.5)

Введем функцию, отражающие суммарные транспортные затраты:

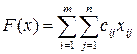. (6.6)

Таким образом, математическая модель данной задачи будет иметь вид:

,

,

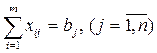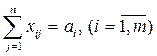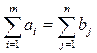, (6.7)

,

.

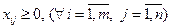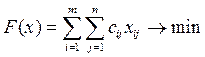Необходимо определить такой план перевозок 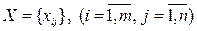, удовлетворяющий системам (6.3), (6.4), условию (10.5), при котором суммарные транспортные затраты будут минимальными, т.е. минимизирующий целевую функцию (6.6).

Примечания:

1) Теорема 6.1. Для того чтобы транспортная задача линейного программирования имела решение, необходимо и достаточно, чтобы выполнялось условие (6.2).

Поэтому если транспортная задача открытого типа, то

а) при 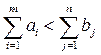(т.е. если суммарная потребность потребителей превышает суммарные запасы складов-поставщиков) вводится фиктивный склад-поставщик, запас которого составляет:

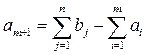. (6.8)

б) при 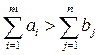(т.е. если суммарные запасы складов-поставщиков превышают суммарную потребность потребителей) вводится фиктивный потребитель, потребность которого составляет

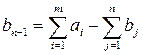. (6.9)

При этом стоимости перевозок для каждой фиктивной пары склад-поставщик – потребитель принимаются, как правило, равными нулю.

2) Теорема 6.2. Ранг r системы уравнений (6.3), (6.4) при условии (6.2) равен:

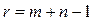. (6.10)

Следовательно, опорный план (базисное решение) транспортной задачи должен содержать 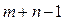отличных от нуля неизвестных. Если в опорном плане число отличных от нуля компонент равно 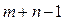, то план является невырожденным, а если меньше – то вырожденным.

3) Рассмотренная транспортная задача является по своей сути целочисленной, так как перевозимые грузы в большинстве случаев представляют собой упаковки, ящики, контейнеры и т.д.

Один из важнейших теоретических результатов исследования операций может быть сформулирован следующим образом:

Теорема 6.3. Если для транспортной задачи (6.7) выполняются условия

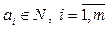и 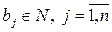, (6.11)

(где N – множество натуральных чисел), то в любом ее допустимом базисном решении базисные переменные принимают значения из множества 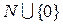, т.е. являются целыми положительными числами или равны нулю.

Поскольку оптимальное решение транспортной задачи (6.7) является допустимым, то при выполнении условий (6.11) оно удовлетворяет требованию целочисленности. Следовательно, условие целочисленности переменных в транспортной задаче (6.7) можно опустить.

4) В модели (6.7) вместо матрицы стоимостей перевозок (С) может задаваться матрица расстояний. В данном случае в качестве целевой функции рассматривается минимум суммарной транспортной работы.

Наиболее распространенным методом решения задач ЛП транспортного типа является метод потенциалов, состоящий из следующих этапов:

1) проверка сбалансированности запасов и потребностей;

2) разработка исходного опорного плана;

3) проверка вырожденности опорного плана;

4) расчет потенциалов;

5) проверка плана на оптимальность;

6) поиск «вершины максимальной неоптимальности» (ВМН);

7) построение контура перераспределения поставок;

8) определение минимального элемента в контуре перераспределения и перераспределение поставок по контуру;

9) получение нового опорного плана.

Этапы 3-9 повторяются, пока не будет найдено оптимальное решение.

Рассмотрим перечисленные этапы.

Дата добавления: 2013-12-12