Статистическая значимость

Тема 4 Основные понятия математической статистики

Задания для самостоятельной работы

Пример построения гистограммы

Кол-во разрядов * Объем разряда ≥ Размах+1

Алгоритм построения диаграммы

1. Упорядочивание выборки, нахождение минимального и максимального значений, определение размаха. Составление таблицы частот для каждого значения.

2. Выбор количества разрядов. Разряд – это несколько близких значений. Рекомендуется, чтобы количество разрядов было в промежутке от 6 до 15. Желательно отсутствие пустых разрядов.

3. Определение объема разряда. Границы разрядов определяются так, чтобы минимальное и максимальное значения попадали в крайние интервалы. При этом необходимо, чтобы произведение количества разрядов на объем разряда превышало показатель размаха по крайней мере на одно значение:

4. Табулирование, то есть составление таблицы распределения частот для каждого интервала значений. Разрешается ситуация, когда минимальное значение выше нижней границы наименьшего интервала, а максимальное значение ниже наибольшего интервала ниже верхней границы наибольшего интервала.

5. Построение графика.

В студенческой группе объемом 42 человека давалось тестовое задание и фиксировалось время его выполнения в секундах. Были получены следующие значения:
{32, 35, 37, 40, 40, 43, 44, 45, 45, 46, 47, 49, 49, 50, 51, 51, 51, 52, 53, 53, 55, 56, 57, 58, 58, 58, 59, 60, 60, 61, 61, 63, 64, 64, 64, 64, 65, 66, 69, 69, 72, 77}.

Задание: необходимо построить диаграмму распределения значений.

1. Х _max = 77`

Х_min = 32`

Размах = 77 - 32 = 45

Значения заносятся в таблицу частот:

значение	частота		значение	частота		значение	частота		значение	частота
										-
	-
	-									-
										-
	-			-
										-
	-						-			-
	-									-
										-
	-
	-			-
							-

2. Определение количества разрядов (столбиков) Допустим, мы их возьмем в количестве равном 10.

3. Сколько необходимо назначить значений в разряде? Допустим, 4.
Но 4 * 10 = 40, то есть произведение количества разрядов на объем разрядов ниже показателя размаха + 1 балл, что не пойдет.

Если мы возьмем количество значений в разряде равным 5, то произведение количества разрядов на показатели интервала превысит показатель размаха более чем на одно значение (5 * 10 = 50), что нас устраивает.

4. Построение таблицы интервалов дает следующий вариационный ряд.

интервал значения	частота
30-34
35-39
40-44
45-49
50-54
55-59
60-64
65-69
70-74
75-79

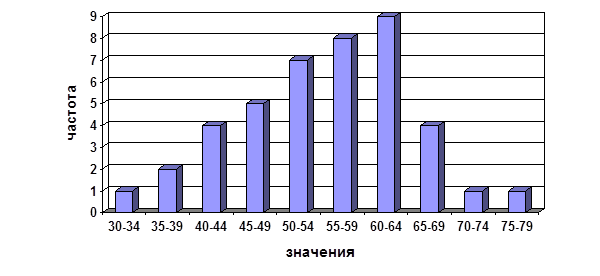
5. По результатам взятым из таблицы строится график.

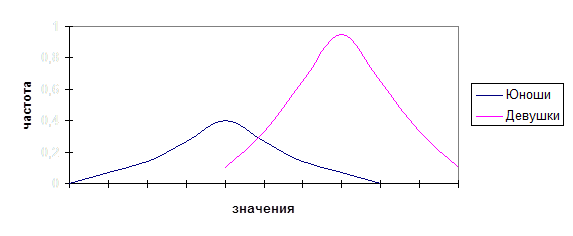
1. Было проведено сравнительное исследование эмоционального реагирования юношей и девушек. По его результатам были построены графики распределения частот, наложенные друг на друга.

Необходимо ответить на следующие вопросы.

1.1. Где на графике ось частоты и ось показателей?

1.2. Какие различия у девушек и юношей по показателям разнообразия паттернов эмоционального реагирования?

1.3. У девушек или юношей в большей степени выражены индивидуальные различия?

2. При исследовании уровня эмоциональной устойчивости в студенческой группе были получены следующие данные: {9, 12, 4, 5, 3, 8, 12, 10, 11, 5, 6, 8, 4, 2, 8, 7, 5, 3, 9, 7, 6, 7, 6, 6}. Задание: построить гистограмму распределения показателей эмоциональной устойчивости. При этом количество разрядов и интервалы значений студентам предлагается назначить самим.

3. Построить гистограмму для данных приведенных в этом параграфе (раздел «Пример построения гистограммы»). При этом количество разрядов назначить равным восьми.

4. Построить гистограмму для показателей роста студентов своей учебной группы. Количество разрядов и интервалы значений студентам предлагается назначить самим.

5. Построить гистограмму для показателей субтестов «осведомленность» и «скрытые фигуры» (Таблица I Приложения). Количество разрядов и интервалы значений студентам предлагается назначить самим.

Уровень достоверности результата исследования (так называемый р - уровень) – это выраженная количественно степень уверенности, что полученные результаты можно распространить на всю популяцию.

Количественные показатели уровня достоверности, называемого также уровнем статистической значимости, находятся в обратной зависимости от надежности результата. То есть чем выше р – уровень, тем ниже надежность и ниже уровень доверия к найденной зависимости. Так, р = 0,05 является более надежным и более желаемым для исследователя значением, нежели чем р = 0,1.

Таким образом, р - уровень показывает вероятность ошибки, связанной с распространением наблюдаемого результата на всю популяцию. Например, р - уровень = 0,05 показывает, что имеется 5 % вероятности, что найденная в выборке связь между переменными является случайной и характерна только для данной выборки.

Существуют различные мнения относительно того, какая величина р - уровня необходима для определения уровня статистической значимости. Например, Е.В. Сидоренко[1] указывает, что зона значимости результатов начинается только после того, как р - уровень достигнет уровня р = 0,01. Но подобные нормативы приняты по неформальному соглашению среди математиков, физиков и экономистов. В гуманитарных же науках большее распространение получила точка зрения, гласящая, что приемлемой границей статистической значимости является результат р £ 0,05. Именно поэтому мы предлагаем пользоваться классификацией предлагаемой А.Д. Наследовым[2], так как считаем ее более удобной и более популярной среди психологов.

Итак, для определения, является ли результат действительно значимым, рекомендуется пользоваться представленной ниже схемой.

Уровень незначимости	Уровень тенденции	Уровень статической значимости	Уровень высокой статистической значимости
	0,1		0,05		0,01

Вероятность ошибки (р - уровень)

Уровень значимости (надежность) результатов

Соотношение показателей р-уровня и степени значимости можно представить также в виде таблицы.

0,1 > р	результаты статистически незначимы
0,05 < р £ 0,1	результаты значимы на уровне тенденции
р £ 0,05	результаты статистически значимы
р £ 0,01	результаты на уровне высокой статистической значимости

Для каждого статистического критерия критические значения р - уровня можно взять из соответствующих специальных таблиц. Знание значения р - уровня необходимо для подтверждения или опровержения статистических гипотез

Дата добавления: 2013-12-12