Скорость. Основные понятия кинематики

Основные понятия кинематики

Механика. Молекулярная физика и термодинамика

Часть I

КУРС ЛЕКЦИЙ ДЛЯ СТУДЕНТОВ-ЗАОЧНИКОВ

Кафедра Физики

Введение. Кинема­ти­ка материальной точки.

(Основные физические модели: материальная точка, система частиц, абсолютно твердое тело, сплошная среда. Задачи кинематики и динамики. Системы отсчета. Траектория, путь, перемещение. Скорость. Ускорение. Вычисление пройденного пути. Тангенциальное и нормальное ускорение. Кривизна траектории. Кинематика вращательного движения. Основные формулы кинематики материальной точки. Связь между векторами линейной скорости и угловой.)

Механическое движение – это изменение с течением времени взаимного расположения тел или их частей.

Кинематика изучает движение тел без рассмотрения причин, обусловливающих это движение.

При описании механического движения используют физические модели материальной точки и абсолютно твердого тела.

Материальная точка – тело, размерами и формой которого можно пренебречь в условиях решаемой задачи. Очевидно, что одно и то же тело в одних условиях можно рассматривать как материальную точку, а в других – только как протяженное тело. Абсолютно твердое тело (часто называют просто твердое тело) – система материальных точек, расстояние между которыми не меняется в процессе движения.

Различные сложные случаи движения твердого тела можно представить как последовательную комбинацию двух основных видов движения:

а) поступательное движение – движение, при котором прямая, проходящая через две произвольные точки твердого тела, всегда остается параллельной своему первоначальному положению;

б) вращательное движение – движение, при котором все точки тела движутся по окружностям, центры которых лежат на одной прямой, называемой осью вращения, а сами окружности лежат в параллельных плоскостях.

Определить положение тела в пространстве, а также изменение этого положения возможно только по отношению к другим телам. Обычно в системе тел выбирают одно, которое служит телом отсчета. Совокупность тела отсчета, связанной с ним системы координат и часов образует систему отсчета (СО). Это понятие является фундаментальным в физике, поскольку пространственно-временное описание движения не имеет смысла, пока не определена СО. Тело отсчета обычно совмещают с началом координат.

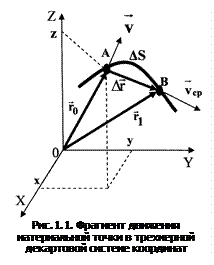
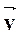
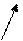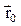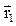На рис.1.1 показан фрагмент движения материальной точки в трехмерной декартовой системе координат (XYZ) из начального положения – (·) А в конечное положение – (·) В. Эти геометрические точки характеризуются соответственно радиусами-векторами и – векторами, проведенными из начала координат в указанные точки. Радиус-вектор любой точки может быть выражен через её координаты (x,y.z):

.

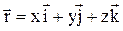Здесь 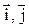и 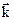– единичные векторы (орты), направленные вдоль координатных осей OX, OY и OZ. Не трудно видеть, что 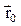и 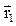связаны между собой соотношением

,

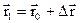где 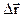- вектор, называемый перемещением. Модуль перемещения равен кратчайшему расстоянию между А и В. Совокупность точек пространства, через которые тело последовательно проходит во время своего движения, называется траекторией. В общем случае это может быть любая трехмерная кривая. В дальнейшем для простоты мы будем в основном рассматривать так называемое плоское движение, при котором траектория лежит в одной определенной плоскости. Длина участка траектории между точками А и В называется путь и обычно обозначается S или ΔS.

Скорость – это векторная физическая величина, характеризующая быстроту перемещения тела в пространстве. Отношение вектора перемещения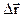к отрезку времени Δt, в течение которого это перемещение произошло, называют средней скоростью:

.

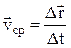Переходя к пределу этого отношения, получим мгновенную скорость:

.

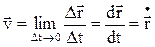Таким образом, мгновенная скорость – векторная величина, определяемая как производная радиуса-вектора движущейся материальной точки по времени. Вектор мгновенной скорости направлен по касательной к траектории в сторону движения. Как и радиус-вектор, вектор скорости может быть разложен на составляющие по осям OX, OY и OZ:

,

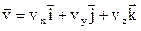где 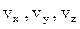– проекции вектора скорости на соответствующие оси. При этом они являются производными координат по времени:

.

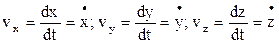Модуль вектора скорости точки:

.

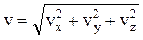При решении многих практических задач используется также средняя путевая скорость – скалярная величина, равная отношению пройденного пути 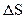к интервалу времени 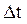, затраченного на его прохождение:

.

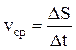Переходя к пределу при 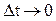и учитывая, что при этом элементарный путь 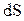бесконечно близок к модулю элементарного перемещения 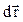, получаем, что модуль мгновенной скорости равен первой производной пути по времени

.

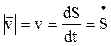Если известен вид зависимости 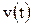, то путь, пройденный точкой за промежуток времени от t ₁ до t ₂, может быть найден путем интегрирования

.

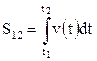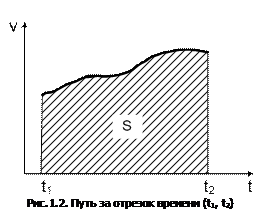Как известно из математического анализа, определенный интеграл численно равен площади фигуры, заключенной между графиком функции и осью аргумента. Поэтому, если задан график скорости, с его помощью может быть численно найден путь за интересующий нас отрезок времени (рис.1.2).

Дата добавления: 2013-12-12