Вращательного движения твердого тела

Момент силы. Уравнение динамики

Кинетическая энергия вращающегося твердого тела

Кинетическая энергия измеряется работой, которую тело может произвести благодаря инерции при затормаживании тела до полной остановки. При вращательном движении роль массы 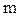выполняет момент инерции 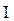, а вместо линейной скорости 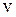выступает угловая скорость , и формула кинетической энергии при вращательном движении тела вокруг неподвижной оси приобретает вид:

.

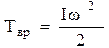В случае плоского движения тела, например цилиндра, скатывающегося с наклонной плоскости без скольжения, кинетическая энергия складывается из энергии поступательного движения и энергии вращения:

,

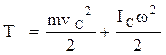где 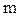- масса катящегося тела; 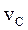- скорость центра масс тела;
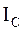- момент инерции тела относительно оси, проходящей через его центр масс; 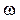- угловая скорость тела.

Моментом силы 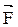относительно неподвижной точки О
называется векторная физическая величина, определяемая векторным произведением радиус-вектора 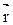, проведенного из точки О в точку А приложения силы, на силу 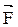(рис.4.3):

.

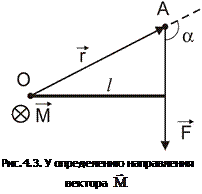
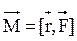Модуль момента силы равен 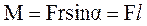, где 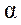– угол между 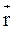и 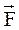, 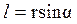- плечо силы 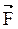(l – длина перпендикуляра, опущенного из точки О на направление действия силы (см. рис. 4.3)).

Направление вектора 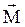совпадает с направлением поступательного движения правого винта при его кратчайшем повороте от 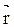и .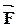

Моментом силы относительно неподвижной оси z называется скалярная величина 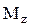, равная проекции на эту ось вектора 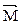момента силы, определенного относительно произвольной точки О данной оси z.

Работа при вращении тела вокруг неподвижной оси zравнапроизведению момента 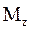действующей силы относительно данной оси на угол поворота :

.

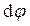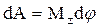Работа при вращении тела идет на увеличение его кинетической энергии:

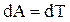, но ,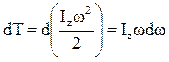

поэтому

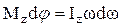или .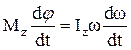

Учитывая, что 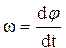, получаем

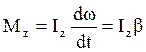. (4.1)

Уравнение (4.1) представляет собой основное уравнение динамики вращательного движения твердого тела относительно неподвижной оси z.

Можно показать, что если ось z совпадает с главной осью инерции (смотри раздел 4.5), проходящей через центр масс, то имеет место векторное равенство

,

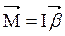где 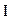- главный момент инерции тела (момент инерции относительно главной оси). Таким образом, направление 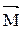совпадает с направлением .

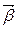Дата добавления: 2013-12-12