Магнитное поле

Затруднения классической теории электропроводности металлов. Сверхпроводимость металлов. Открытие высокотемпературной сверхпроводимости.

Закон Видемана-Франца.

Из опыта известно, что металлы, наряду с высокой электропроводностью, обладают также высокой теплопроводностью. Видеман (Wiedemann G., 1826-1899) и Франц (Franz R.,) установили в 1853г. эмпирический закон, согласно которому отношение коэффициента теплопроводности κ к коэффициенту электропроводности σ для всех металлов приблизительно одинаково и изменяется пропорционально абсолютной температуре:

.

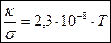Рассматривая электроны как одноатомный газ, можем на основании кинетической теории газов написать для коэффициента теплопроводности электронного газа:

,

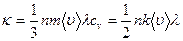где 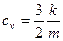- удельная теплоемкость одноатомного газа при постоянном объеме.

Разделив κ на σ, приходим к закону Видемана-Франца:

.

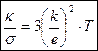Подставив сюда k = 1,38·10^-23 Дж/К и е = 1,6·10^-19 Кл, найдем, что

,

что очень хорошо согласуется с экспериментальными данными.

Несмотря на достигнутые успехи, классическая электронная теория проводимости металлов Друде-Лоренца не получила дальнейшего развития. Связано это с двумя основными причинами: 1) трудностями, с которыми столкнулась эта теория при объяснении некоторых свойств металлов; 2) созданием более совершенной квантовой теории проводимости твердых тел, устранившей затруднения классической теории и предсказавшей ряд новых свойств металлов.

Выделим основные затруднения теории Друде-Лоренца:

1. Согласно классической теории,зависимость удельного сопротивления металлов от температуры 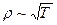в то время, как на опыте в широком интервале температур вблизи Т≈300К для большинства металлов наблюдается зависимость ρ ~ Т.

2. Хорошее количественное совпадение с законом Видемана-Франца оказалось в известной степени случайным. В первоначальном варианте теории Друде не учитывал распределение электронов по скоростям. Позже, когда Лоренц учел это распределение, оказалось, что отношение

,

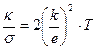что значительно хуже согласуется с экспериментом. Согласно же квантовой теории,

.

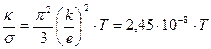3. Теория дает неправильное значение теплоемкости металлов. С учетом теплоемкости электронного газа С=9/2R, а на практике С=3R, что примерно соответствует теплоемкости диэлектриков.

4. Наконец, теория оказалась полностью неспособной объяснить открытое в 1911г. Камерлинг-Оннесом (Kamerligh-Onnes H., 1853-1926) явления сверхпроводимости (полного исчезновения сопротивления) металлов при низких температурах, а также существования остаточного сопротивления, в сильной степени зависящего от чистоты металла (рис.6.4).

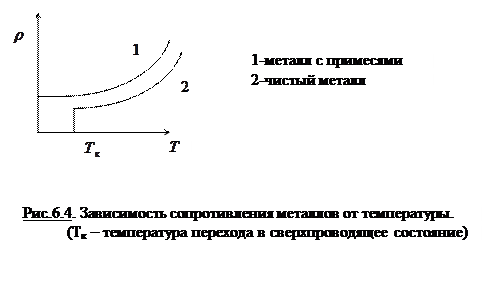
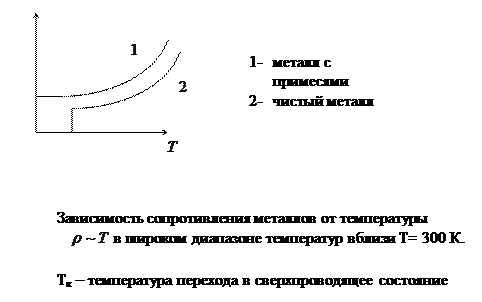
Интересно отметить, что в отношении низкотемпературных сверхпроводников (металлов) действует правило: металлы с более высоким удельным сопротивлением ρ имеют и более высокую критическую температуру сверхпроводящего перехода Т_кр (см. таблицу

Таблица. Свойства низкотемпературных сверхпроводников.

Металл	Удельное сопротивление, 10^-8 Ом∙м	Тк , К
Титан Алюминий Ртуть Свинец	1,7 2,5	0,4 1,2 4,1 7,2

Феноменологическая теория низкотемпературной с верхпроводимости была создана в 1935г. Ф.и Г. Лондонами (London F., 1900-1954, London H., 1907-1970), но лишь спустя почти полвека (в 1957г.) явление сверхпроводимости получило окончательное объяснение в рамках микроскопической (квантовой)теории, созданной Дж.Бардиным, Л. Купером и Дж. Шриффером (Bardeen J., Cooper L., Schrieffer J.).

В 1986г. Дж. Беднорцем (Bednorz J.) и К. Мюллером (Müller K.) было открыто явление высокотемпературной сверхпроводимости в керамических металлоксидах (лантана, бария и др. элементов), являющихся диэлектриками при комнатнойтемпературе. Критическая температура перехода в сверхпроводящее состояние для этих материалов около 100К.

Теория высокотемпературной сверхпроводимости в настоящее время находится в стадии разработки и пока далека от своего завершения. Неясен даже механизм возникновения высокотемпературной сверхпроводимости.

(Магнитное поле. Опыты Эрстеда. Силовое действие магнит­ного поля. Взаимодействие токов. Закон Био-Савара-Лапласа. Индукция магнитного поля. Поле прямого и кругового токов. Вихревой характер магнитного ноля. Поле движущегося заряда. Циркуляция вектора индукции магнитного поля.)

Магнитостатика.

Магнитное взаимодействие токов

Рассмотрим такой эксперимент. Возьмем два гибких проводника и подвесим их на небольшом расстоянии друг от друга (см. рис. 3.1).

В первом случае (рис. 3.1.а) проводники свободно располагаются в поле силы тяжести Земли. Т.к. размеры проводников гораздо меньше размеров Земли, то они расположатся параллельно друг другу. Однако каждый из этих проводников обладает массой, и, следовательно, они должны притягиваться друг к другу по закону всемирного тяготения (I.1.31). Но отклонений от их прямолинейности мы не заметим. Т.е. гравитационные силы взаимодействия между проводниками слишком малы.

Во втором случае (рис. 3.1. b) эти же проводники, находящиеся на том же расстоянии друг от друга, мы подключим к полюсам источника тока. Следовательно, на проводниках появятся электрические заряды противоположного знака и они должны притягиваться друг к другу. Однако и в этом случае мы не заметим никакого отклонения от параллельности проводников. Следовательно, и силы электростатического взаимодействия слишком малы.

В третьем случае (рис. 3.1.с) противоположные концы проводников мы перемкнули, так, что по проводникам потекли токи противоположного направления. В этом случае мы сразу же заметим отклонение от параллельности проводников ‑ они будут отталкиваться друг от друга (в противоположность разноименным электрически заряженным телам, которые притягиваются).

В четвертом случае (рис. 3.1.d) проводники к источнику тока мы подключили так, что по ним потекли токи одного направления. В этом случае мы также сразу увидим их взаимодействие ‑ они будут притягиваться друг к другу (в противоположность одноименным зарядам, которые отталкиваются).

Поскольку это, как мы видели, ни гравитационное, ни электростатическое взаимодействие, мы вынуждены заключить, что обнаружили новый, не известный ранее, тип взаимодействия. И это взаимодействие осуществляется посредством электрического тока, т.е. посредством движущихся зарядов.

Являясь сторонниками теории близкодействия, мы вынуждены заключить, что вокруг проводника с током возникает поле, которое действует на другой проводник с током.

В дальнейшем Эрстед проводил подобные опыты с токами и обнаружил, что около проводников с током магнитная стрелка отклонялась от своего первоначального направления. Т.е. поле, возбуждаемое токами, действует на магнитную стрелку. Поэтому поле вокруг токов назвали магнитным полем.

Магнитное поле, его характеристики

Итак, вокруг проводников с током существует магнитное поле. Оно объективно, поскольку существует независимо от наших знаний о нем. Оно материально, поскольку действует на материальные тела.

Теперь встает задача об исследовании свойств этого поля. Основное свойство магнитного поля ‑ это действовать на проводники с током. Поэтому для исследования свойств магнитного поля необходимо использовать проводник с током. Но если при исследовании электростатического поля мы использовали пробные, точечные электрические заряды, то в данном случае ситуация сложнее. Технически невозможно создать очень маленький отрезок проводника с током. Поэтому для исследования свойств магнитного поля используют контур с током достаточно малого размера, в пределах которого исследуемое магнитное поле можно считать однородным.

Оказалось, что при внесении в магнитное поле пробного контура, он не перемещается в пространстве (как заряды в электрическом поле), а лишь поворачивается на некоторый угол и останавливается в этом положении равновесия. Следовательно, суммарная сила, действующая на контур с током со стороны магнитного поля равна нулю. В то же время вращающий момент, действующий на контур с током, в общем случае отличен от нуля.

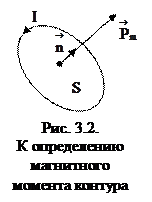Поэтому, для количественной характеристики магнитного поля стали использовать механический вращающий момент 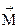, действующий на контур. Но этот вращающий момент зависит также и от свойств самого контура ‑ силы тока в нем, площади контура и т.д. При дальнейших исследованиях выяснилось, что этот вращающий момент совершенно не зависит от формы контура, а определяется его площадью. Кроме того, вращающий момент зависит также от величины силы тока, текущего в пробном контуре. Поэтому сам контур стали характеризовать величиной, равной произведению силы тока 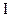в контуре на его площадь 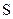. Эту величину обозначают символом 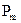и называют магнитным моментом контура 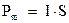. Магнитный момент контура векторная величина. Он направлен перпендикулярно плоскости контура и связан с направлением обхода тока контура правилом правого буравчика. Если обозначить направление положительной нормали к плоскости контура как 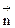, то вектор магнитного момента контура с током будет определяться:

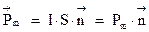(3.1)

Таким образом, по аналогии с электростатикой, магнитное поле стали характеризовать отношением вращающего момента, действующего на контур с током, к величине магнитного момента самого контура.

Но мы отмечали, что этот вращающий момент не постоянен. При равновесном положении контура он вообще равен нулю. Поэтому за характеристику магнитного поля принимают отношение максимального вращающего момента 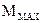к магнитному моменту контура. Это отношение обозначают символом 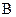и называют индукцией магнитного поля:

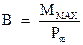(3.2)

Из (3.2) вытекает размерность индукции магнитного поля:

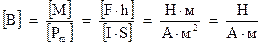
За единицу индукции магнитного поля принимают индукцию такого поля, в котором на контур площадью 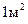при силе тока в нем 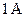, действует максимальный вращающий момент сил, равный 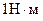. Эта единица индукции магнитного поля получила название тесла (Тл). Таким образом .

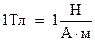Но индукция магнитного поля векторная величина. Вектор индукции магнитного поля направлен по направлению вектора магнитного момента контура с током (по направлению положительной нормали к контуру) в месте его равновесного положения в поле.

Силовые линии магнитной индукции, поток вектора магнитной индукции

Наглядно магнитное поле, также как и электрическое, изображают с помощью линий магнитной индукции.

Непрерывные линии, касательные к которым в каждой точке, через которую они проходят, совпадают с вектором индукции, называются силовыми линиями магнитного поля.

Силовые линии обладают следующими свойствами.

1). Силовые линии магнитного поля замкнуты ‑ они не имеют ни начала, ни конца.

2). Линии непрерывны и нигде не пересекаются (т.к. их пересечение означало бы отсутствие определенного направления индукции магнитного поля в данной точке).

3). Густота линий выбирается так, чтобы количество линий, пронизывающих единицу поверхности площадки, перпендикулярной к линиям, было равно численному значению (модулю) вектора .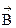

Как видим, основное отличие от линий напряженности электрического поля состоит в том, что линии магнитной индукции замкнуты, не имеют ни начала, ни конца. Это означает, что в природе нет магнитных зарядов, на которых линии могли бы начинаться или заканчиваться. Действительно, из опыта мы знаем, что существуют постоянные магниты. Они всегда обладают двумя полюсами ‑ северным и южным. Но их всегда два. Сколько раз мы бы не распиливали магнит, всегда, в сколь угодно маленьком магните будут существовать два полюса. Магнитных унизарядов, униполюсов в природе нет. Это фундаментальное свойство нашей вселенной.

В дальнейшем мы покажем, что поля, обладающие таким свойством, являются вихревыми полями.

На рис. 3.3 показаны силовые линии прямолинейного проводника с током, представляющие собой концентрические окружности с центром на оси проводника. На рис. 3.4 показаны силовые линии кругового кольца с током и на рис. 3.5 силовые линии соленоида (длинная катушка).

Найдем теперь выражение для потока 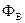вектора магнитной индукции 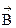через произвольную замкнутую поверхность .

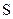Отсутствие в природе магнитных зарядов приводит к тому, что, как мы отмечали, линии магнитной индукции не имеют ни начала, ни конца. Поэтому число пересечений, возникающих при входе линий индукции в объем, ограниченный поверхностью 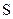, всегда равно числу пересечений линий магнитной индукции, возникающих при выходе из этого объема. Следовательно, для любого поля и любой произвольной поверхности всегда выполняется условие:

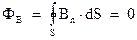(3.3)

Из выражения (3.3) вытекает размерность потока магнитной индукции:

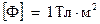
У этой единицы есть специальное наименование ‑ вебер (Вб): .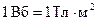

Выражение (3.3) представляет собой теорему Гаусса для магнитного поля:

поток вектора магнитной индукции через замкнутую поверхность равен нулю.

Уравнение (3.3), также как и уравнение (1.27), является одним из четырех уравнений Максвелла в интегральной форме.

Также как и для электрического поля, выражению (3.3), являющемуся теоремой Гаусса в интегральной форме, соответствует представление в дифференциальной форме. Вывод этой формулы аналогичен для электрического поля, поэтому приводить его мы не будем, а сразу запишем конечный результат:

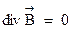(3.4)

Уравнение (3.4), также как и уравнение (1.28), является одним из четырех уравнений Максвелла в дифференциальной форме.

Закон Био-Савара, поле движущегося заряда

Ученые Био и Савар производили эксперименты с магнитными полями, возбуждаемыми проводниками с током различной формы. Лаплас, произведя математический анализ их результатов, нашел, что магнитное поле любого тока может быть вычислено как векторная сумма полей, создаваемых отдельными, элементарными участками тока.

Если по проводнику, длиной 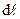течет ток силой 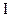, то индукцию магнитного поля, создаваемого этим током, можно рассчитать по формуле:

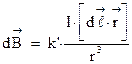
Направление вектора 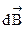определяется согласно правилу векторного произведения векторов: если вектор 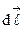вращать к вектору 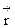в сторону меньшего угла, то поступательное движение правого винта покажет направление вектора 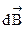. Коэффициент 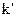‑ коэффициент, необходимый для уравнивания размерностей. В СИ этот коэффициент принято писать в виде 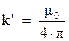. Константу 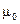называют магнитной постоянной. Следовательно, в СИ закон Био-Савара будет иметь вид:

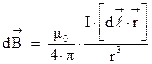(3.5)

Соответственно, скалярная форма закона Био-Савара будет иметь вид:

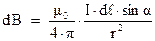(3.6)

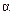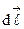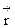Здесь ‑ угол между векторами и . Магнитная постоянная будет иметь следующую размерность:

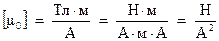
Позже, на основании закона Ампера, мы найдем численное значение магнитной постоянной .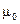

Далее, электрический ток представляет собой направленное, упорядоченное движение заряженных частиц. Следовательно, магнитное поле тока ‑ это сумма магнитных полей, создаваемых каждым движущимся зарядом. Найдем, исходя из закона Био-Савара, выражение магнитного поля, создаваемого отдельным, движущимся зарядом. Для этого в уравнении (3.5) раскроем произведение :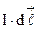

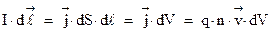
Здесь было использовано выражение (2.4) для плотности тока. Произведение числа частиц в единице объема 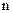на величину объема 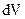даст общее число носителей тока 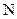, т.е. общее число заряженных частиц, создающих магнитное поле. Поэтому последнее равенство перепишем в виде: 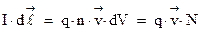. Подставляя полученное выражение в закон Био-Савара, можно записать:

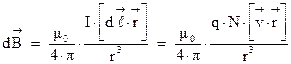
Разделив левую и правую части уравнения на число заряженных частиц, мы получим выражение для расчета магнитного поля, создаваемого отдельной заряженной частицей:

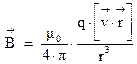(3.7)

Отметим, что уравнение (3.7) справедливо для случая, когда заряды движутся со скоростью, много меньшей скорости света .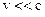

Рассмотрим теперь применения формулы (3.5).

Магнитное поле прямого тока

Рассмотрим бесконечно длинный проводник, по которому течет ток силой 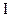(см. рис. 3.6). Точка наблюдения 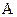, в которой мы должны рассчитать вектор индукции магнитного поля, находится на расстоянии 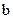от проводника с током. Согласно рис. 3.6, можно заключить, что вектор индукции справа от проводника везде направлен от нас за чертеж, а слева ‑ из-за чертежа к нам. Следовательно, направление вектора магнитной индукции будем считать известным. Поэтому для расчета поля можно воспользоваться скалярной формой записи уравнения Био-Савара (3.6) ‑ 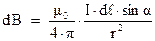. Однако сразу это уравнение интегрировать нельзя, т.к. здесь слишком много переменных ‑ 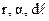. Выразим переменные 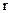и 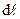через переменную .

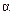Согласно рис. 3.6, можно записать:

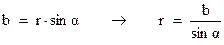
Далее, согласно рис. 3.6, можно записать:

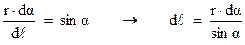
Воспользовавшись значением 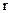, последнее равенство перепишем в виде:

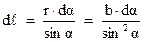
Подставив найденные значения переменных в (3.6), получим:

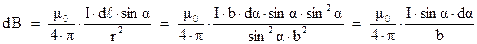
Получившееся уравнение уже можно интегрировать по переменной 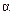. Когда элемент тока 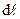будет находиться «бесконечно далеко» внизу, угол 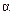будет стремиться к нулю. Т.е., нижний предел интегрирования ‑ 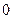. Аналогично, когда элемент тока 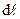будет находиться «бесконечно далеко» вверху, угол 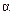будет стремиться к 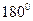. Следовательно, верхний предел интегрирования ‑ 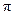. Таким образом, индукция магнитного поля в точке наблюдения 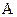будет рассчитываться как:

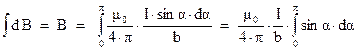
Произведя интегрирование, получим:

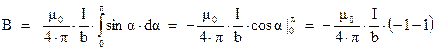
Или, окончательно:

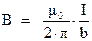(3.8)

Следовательно, модуль индукции магнитного поля, создаваемого бесконечно длинным, прямолинейным проводником с током, прямо пропорционален силе тока в проводнике и обратно пропорционален расстоянию до проводника.

Рассчитаем теперь индукцию магнитного поля, создаваемого током, текущим по круговому проводу.

Индукция магнитного поля кругового витка с током

Рассмотрим проводящее кольцо, радиуса 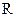, по которому течет ток силой 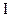(см. рис. 3.7). Рассчитаем индукцию магнитного поля этого проводника с током в точке наблюдения 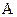, лежащей на оси симметрии кругового витка, на расстоянии 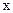от его плоскости (см. рис. 3.7). На проводнике с током выделим элемент 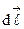, направленный в верхней части контура из-за чертежа к нам. Расстояние от этого элемента до точки наблюдения обозначим через 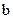. Ясно, что в какой бы точке контура не находился бы элемент 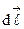, он всегда будет перпендикулярен прямой 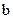. Т.е. угол 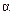в уравнении (3.6) всегда равен 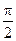и, соответственно, 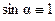. Поэтому для нашего случая уравнение (3.6) будет иметь вид:

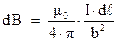
поскольку для нашего случая расстояние 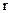это есть именно .

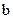Вектор индукции 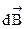, согласно правилу векторного произведения, перпендикулярен элементу 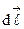, т.е. находится в плоскости чертежа (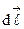, как отмечалось, перпендикулярен плоскости чертежа). Кроме того, 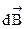перпендикулярен также и прямой 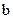(см. рис. 3.7).

Разложим этот вектор на две составляющие: составляющую 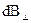‑ перпендикулярную оси симметрии кольца, и составляющую 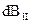‑ параллельную оси симметрии кольца.

Из рисунка 3.7 ясно видно, что составляющие 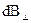, от диаметрально противоположно расположенных элементов 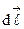, будут взаимно компенсироваться. Т.е. при интегрировании по всему кольцу эта компонента поля исчезнет.

И наоборот, компоненты 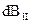будут складываться. Поэтому дальше мы будем рассчитывать только параллельную оси симметрии кольца компоненту поля. Из рисунка также вытекает, что 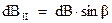. А синус угла 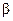в свою очередь равен 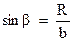. Поэтому, для индукции магнитного поля, генерируемого элементом контура 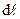вдоль оси симметрии, получается следующее выражение:

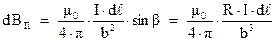
Чтобы найти результирующее поле, необходимо проинтегрировать по всему кольцу:

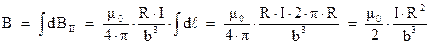
Обычно это выражение записывают в виде:

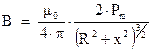(3.9)

где 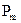‑ магнитный момент кольца: .

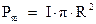Если точка наблюдения находится в центре кольца (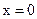), то выражение для индукции примет вид:

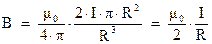(3.10)

И наоборот, если точка наблюдения находится очень далеко от плоскости кольца (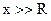), то выражение для индукции магнитного поля будет иметь вид:

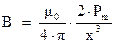(3.11)

Необходимо помнить, что во всех случаях вектор магнитной индукции направлен так же, как и магнитный момент кольца.

Вихревой характер магнитного поля

Выше частично мы уже касались этого вопроса. Мы говорили о том, что силовые магнитного поля всегда замкнуты и не имеют ни начала, ни конца. В то время как линии электростатического поля имеют начало и конец. Мы также говорили о том, что электростатическое поле ‑ потенциальное поле и вводили в рассмотрение потенциал поля, согласно формуле (1.15). Другим выражением потенциальности электростатического поля было равенство нулю циркуляции вектора напряженности поля (см. (1.12), (1.13)).

Поскольку свойства линий магнитной индукции кардинально отличаются от свойств линий электрической напряженности, то можно предположить, что магнитное поле не потенциальное поле. Для решения этого вопроса посчитаем циркуляцию вектора индукции магнитного поля. Т.е. посчитаем, чему равно выражение .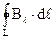

В связи с этим, рассмотрим простейший случай магнитного поля, которое 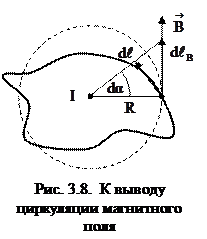создается прямолинейным, бесконечно длинным проводником с током 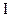. Причем циркуляцию будем считать по контуру, плоскость которого перпендикулярна току (см. рис. 3.8). Ток направлен из-за чертежа к нам. В каждой точке контура, находящейся на некотором расстоянии 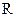от тока, вектор индукции 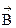направлен перпендикулярно радиус-вектору, в направлении против часовой стрелки (т.к. ток направлен к нам). Или по касательной к окружности радиуса 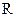, которую мы проведем из места нахождения тока (см. рис. 3.8).

Согласно правилу скалярного произведения векторов, произведение 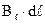, можно заменить на произведени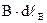е , где 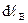‑ проекция вектора 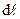на направление вектора 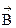. Но согласно тригонометрическому определению центрального угла, величину 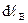можно заменить на произведение 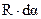(см. рис. 3.8). Т.е. можно записать .

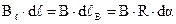Таким образом, выражение для циркуляции магнитного поля будет иметь вид:

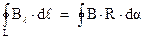
Т.к. магнитное поле создается прямолинейным проводником с током, то необходимо воспользоваться выражением (3.8):

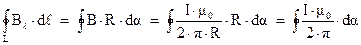
Поскольку интегрирование ведется по всей окружности, то 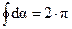. Поэтому окончательно, для циркуляции магнитного поля мы получим выражение:

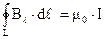(3.12)

Циркуляция магнитного поля равна току внутри контура, умноженному на магнитную постоянную .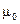

В теоретической физике доказывается, что эта формула справедлива и в случае произвольной формы контура и пересекающего его тока.

Очевидно, что если внутри контура будет не один ток, а несколько, то аналогичные рассуждения можно провести для каждого тока, и в результате получить:

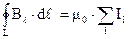(3.13)

Циркуляция магнитного поля равна сумме токов внутри контура, умноженной на магнитную постоянную 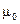. Причем для токов нужно различать положительное и отрицательное направления.

Если ток распределен непрерывно по площади сечения контура (как, например, в случае проводящей жидкости), то формула (3.13), аналогично формуле (1.6), примет вид:

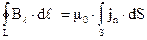(3.14)

Эта формула является более общим выражением для циркуляции магнитного поля. Она является одним из уравнений Максвелла в интегральной форме, в случае постоянных полей (не меняющихся с течением времени). Также как и уравнению (1.12), уравнению (3.14) соответствует дифференциальная форма записи:

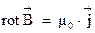(3.15)

Уравнение (3.15) является одним из уравнений Максвелла в дифференциальной форме, в случае постоянных полей (не меняющихся с течением времени)

Дата добавления: 2013-12-12