Решение волнового уравнения в случае плоской электромагнитной волны в вакууме

Волновое уравнение в случае вакуума.

Уравнения Максвелла для электромагнитных волн в вакууме.

Нормальные электромагнитные волны в вакууме – это поля, которые могут существовать в отсутствии источников.

Будем рассматривать нормальные волны (т.е. без учёта источников). Уравнения Максвелла в вакууме имеют вид:

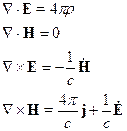
Величины 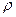и 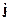определяют свойства источников поля. Нормальные волны существуют без источников, тогда здесь уравнения Максвелла:

□

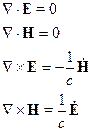
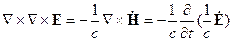
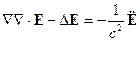
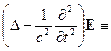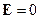
Аналогично уравнение получаем для :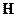

□

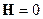
Здесь будем использовать калибровку поперечных волн (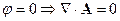), т.к. в вакууме электромагнитные волны плоские поперечные волны. Тогда:

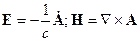
Волновое уравнение для :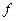

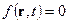
Где 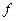- это различные компоненты векторов .

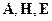Волна плоская, т.к. фронт распространения волны представляет собой плоскость.

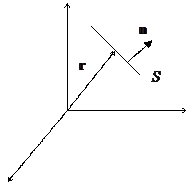
Имеем систему координат, точку на фронте волны ,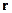

нормаль к фронту волны 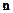. Тогда уравнение фронта волны (т.е. плоскости): 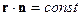. Но т.к. эта плоскость движется, то появляется зависимость от времени.

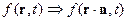
Если фронт волны- сфера, т.е. волна сферическая, то уравнение фронт а волны 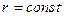и:

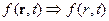
Учтём обстоятельство, что форма фронта волны налагает на 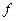некоторые ограничения. Введём некоторые вспомогательные координаты:

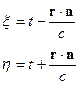
И будем упрощать оператор □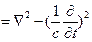. Можно перейти от (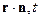) к (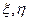). Рассчитаем 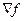и 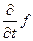, где функция 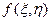- сложная.

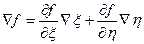
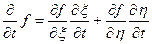
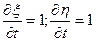
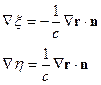
Рассмотрим компоненту: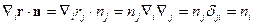. Тогда:

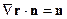
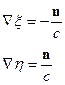
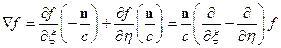
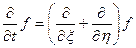
Следовательно:

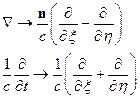
Это для случая плоской монохроматической волны. В результате имеем:

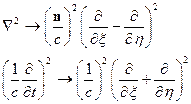
Тогда оператор □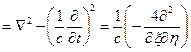

Итак, □ 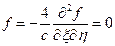, тогда .

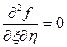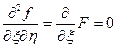
где 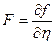. Следовательно,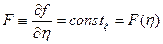

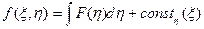
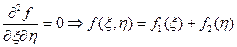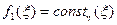Тогда , где и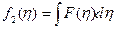

Выясним, как происходит движение фронтов волны для 1 и для 2 случаев:

1 случай:

,

(*)

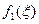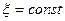
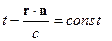Получили, что фронт волны перемещается. Продифференцируем (*) по времени:

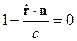
где 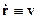- фазовая скорость. Тогда 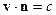. Для среды 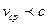, для вакуума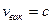

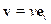, тогда 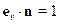. Для вакуума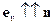

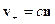
2 случай:

,

(**)

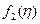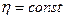
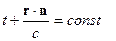Продифференцируем (**) по времени:

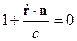
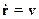- фазовая скорость

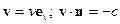
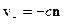
И мы поучили, что фронт волны распространяется в обе стороны. Если волна не встречает препятствий, то решение - 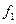и 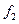, иначе решение усложняется.

Дата добавления: 2013-12-12