Лекция № 3

Введение

Курс лекций. Часть 1.

Теплотехнические измерения и приборы.

Курс ТТИП охватывает вопросы теории и техники измерения величин, характеризующих теплотехнические процессы – .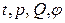

История развития ТИП связана с общим развитием промышленности. Первые теплотехнические приборы – водяной термометр Галилея (1697) и ртутный барометр Торричелли (1643) – использовались в основном для научных целей, в промышленности преобладала ориентация на профессиональное мастерство и опыт (температуру – на ощупь, зазор – пальцем и т.п.). Заметное использование измерительных приборов (ИП) в промышленности началось только в ХХ веке в связи с внедрением более совершенного технологического оборудования, а также с развитием автоматизации производственных процессов.

С измерительной техникой связаны две группы задач:

1) комплексная автоматизация производства; и

2) усиление роли науки.

1 – нельзя автоматизировать процессы, которые не поддаются измерению.

2 – Менделеев Д.И. «Наука начинается там, где начинают измерять».

Задачи курса ТТИП:

1) изучение и критическое сопоставление методов измерения различных величин, характеризующих теплотехнические процессы;

2) рассмотрение основных конструктивных схем измерительных устройств;

3) оценка возможной достоверности измерения (погрешность).

4)

Глава 1 Общие сведения об измерениях

1.1 Основные характеристики измерений.

Теоретической основой измерительной техники является метрология (от греч. metron – мера, и logos – учение, понятие) – это наука об измерениях, методах и средствах обеспечения их единства и способах достижения требуемой точности.

Единство измерений необходимо для возможности сопоставления, сравнения результатов измерений.

Сравнить можно физические объекты по принципу «больше – меньше», как-то: длиннее или короче, тяжелее или легче, теплее или холоднее и т.п. Такие физические величины называют однородными.

Последовательный ряд из постепенно увеличивающихся однородных ФВ называется натуральным рядом.

Для формирования шкалы (от лат. scalae – лестница) ФВ из последовательного натурального ряда выбирают реперные точки (от фр. repere – столб, рейка) 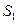и .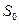

Расстояние между размерам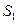и и 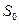называют основным интервалом, один из размеров – 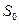– принимают за начало отсчета, а некоторую n -ю долю этого интервала за единицу ФВ: .

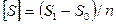Выбор 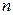в принципе произволен (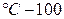, 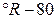), т.о. размеры ФВ определяются методом линейной интерполяции. Физически это реализуется методом измерительных преобразований, т.к. ФВ не может быть определена сама по себе, а воспринимается только через тот физический процесс, в котором она проявляется. Измерительные преобразования (ИП) позволяют осуществлять интерполяцию размеров ФВ между реперными точками и определить протяженность основных интервалов. На основе ИП строится функциональная ФВ.

Измерение – это определение ФВ опытным путем с помощью специальных технических средств. Измерения осуществляются обычно на естественных и искусственных объектах измерений (ОИ).

ОИ – это явление или процесс, который характеризуется отдельными параметрами ФВ, каждая из этих ФВ может быть измерена отдельно. ФВ, которая выбрана для измерения, называется измеряемой величиной.

Процесс измерения ФВ включает в себя три этап а:

подготовку, проведение измерения или измерительного эксперимента и обработку его результатов.

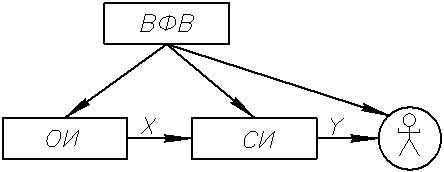
Схема процесса измерения величины Х

Основные уравнения измерения: ,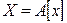

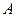– числовые значения ФВ;

– единица физической величины.

Средством измерения (СИ) называется техническое средство и имеющее нормированные технологические характеристики.

Размер ФВ существует реально, числовое значение А зависит от выбора единицы ФВ.

Различают истинное и действительное значение ФВ.

Истинное – значение ФВ, которое реально отражало бы ОИ, действительные – измеренные, найденные экспериментально, близкое к истинному и используется вместо него. Истинное недостижимо.

СИ представляет измерительную информацию в виде некоторого сигнала. В процессе измерения на СИ, ОИ и на оператора воздействуют различные внешние факторы – ВФВ (влияние физических величин). Измерения производятся на основе физических явлений, определяющих принцип измерения.

Метод измерения – совокупность приемов и правил использования принципов и средств измерения и средств измерения.

Несовершенство изготовления СИ, неточность их градуировки, действие ВФВ (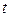, , 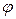электромагнитный импульс, вибрация и т.д.), субъективные ошибки оператора и ряд других факторов обуславливают неизбежное появление погрешностей.

Погрешность (или ошибка) измерения – отклонение результата измерения Х от истинного значения 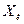измеряемой величины:

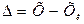– абсолютная погрешность ;

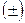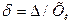– относительная погрешность измерения .

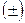Точность измерения отражает степень приближения к истинному значению: .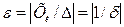

1.2 Классификация измерений осуществляется по 5 признакам.

1.

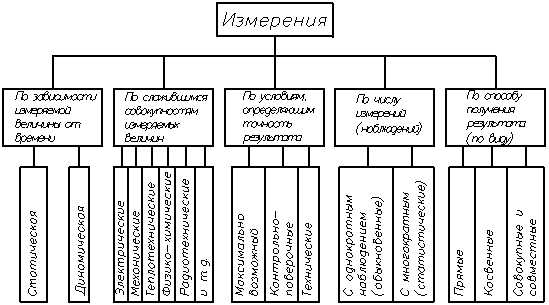
Статические – измеряемая величина остается постоянной во времени.

Динамические – измеряемая величина изменяется в процессе измерения (мгновенные значения).

2. Родственные ФВ в отдельных областях науки и техники.

3. Измерения максимально возможной точности достижимой при современном уровне техники (эталоны, например, универсальные физические константы).

Контрольно-поверочные измерения, их погрешности не должны превышать заданные значения, осуществляются государством и ведомственными метрологическими службами.

Технические измерения – их погрешность определяются характеристиками СИ.

Технические измерения наиболее распространенные, выполняются во всех отраслях хозяйства и науки.

4. Обыкновенные и статистические измерения.

Под наблюдением при измерении понимается экспериментальная операция измерения, в результате которой получают одно значение ФВ.

5. Прямыми называются измерения, при которых, искомые значения находят непосредственно по показаниям приборов: .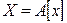

Непрямыми называются измерения, при которых искомые значения находят на основании известной зависимости между этой величиной и величинами, подвергаемыми прямым измерениям: .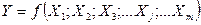

Совокупными называют производимые одновременно измерения нескольких одноименных величин, при которых искомые значения величины находят решением системы уравнений:

;

;

………………………………………………

;

………………………………………………

.

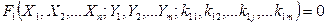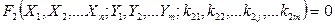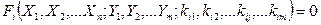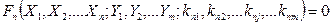где 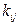– известные величины; 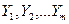– одноименные величины, значения которых являются искомыми; 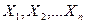– результаты прямых измерений.

Совместными называют проводимые одновременно измерения двух или нескольких неодноименных величин для нахождения зависимости между ними. Описываются такой же системой уравнений, только 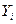– неодноименные величины. Целью совместного измерения является определение функциональной зависимости между величинами .

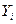Измерения, кроме того, можно разделять в зависимости от места проведения – лабораторные и промышленные, модельные и натурные, времени – непрерывные и периодические и т.д.

1.3 Методы измерений

Методы прямых измерений являются общими для всех видов измерений.

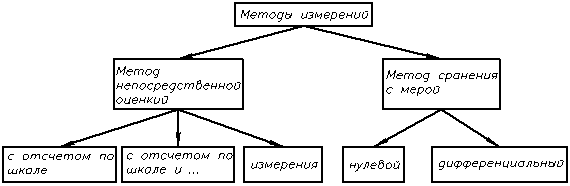
Метод непосредственной оценки (МНО) – метод измерений, в которых значение ФВ определяют непосредственно по отсчетному устройству измерительного прибора прямого действия.

Метод сравнения с мерой – метод измерения, в котором измеряемую величину сравнивают с величиной, воспроизводимой мерой.

Нулевой метод – это метод сравнения с мерой, в котором результирующий эффект воздействия на прибор сравнен (компаратор) доводят до нуля.

Дифференциальный метод – это метод сравнения с мерой, в котором на измерительный прибор воздействует разность между измеряемой величиной и известной, воспроизводимой мерой.

1.4 Погрешности измерений

Т. к. истинное значение ФВ всегда остается неизвестным, то и истинное значение погрешности также нельзя определить. Для приближенной оценки погрешности используют понятие действительного значения ФВ, которое находят более точными методами и средствами. Получаемую оценку погрешности 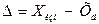в зависимости от причин возникновения, характера и условий проявления выражают суммой двух составляющих – случайной 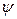и систематической 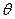погрешности измерений: .

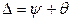Случайная погрешность измерения – составляющая погрешности измерения, изменяющаяся случайным образом при повторных измерениях одной и той же величины.

Случайная погрешность не может быть исключена из результата измерений. Однако проведением ряда повторных измерений и использованием для их обработки методов математической статистики определяют значение измеряемой величины со случайной погрешностью, меньшей, чем для его измерения.

При примерно одинаковом уровне интенсивности действующих факторов находят ожидаемую погрешность.

Грубой погрешностью называют погрешность измерения, существенно превышающая ожидаемую при данных условиях. Причина – неисправность средств измерения, резкое изменение условий измерения и ВФВ.

Промах – погрешность измерения, которая явно и резко искажает результат. Промах является случайной субъективной ошибкой оператора.

Грубые ошибки и промахи исключаются из экспериментальных данных, подлежащих обработке.

Отдельные значения случайной погрешности предсказать невозможно, однако их совокупность подчиняется вероятностным закономерностям. Для количественной оценки возможности появления СП (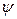) вводится понятие вероятности (достоверное – 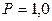, невозможное – ).

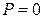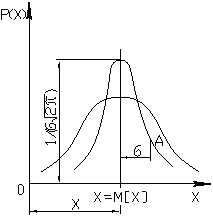
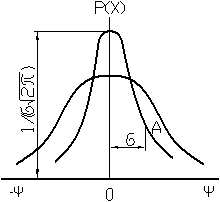
Связь между значениями случайной величины и соответствующими им плотностями вероятностей выражается дифференциальными законами распределения. Наиболее распространенным при измерениях является нормальный закон распределения.

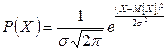
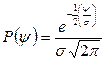
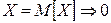
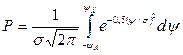
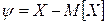
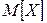– математическое ожидание случайной величины (наиболее достоверное значение);

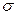– среднеквадратическое отклонение;

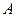– точка перегиба кривой распределения;

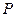– вероятность попадания результата измерения или случайные погрешности в некотором наперед заданном интервале от 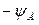до .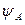

Интервал аналитически не решается, поэтому приводятся табличные значения функции Лапласа. Чаще решается обратная задача в определении доверительного интервала. Доверительный интервал с границами 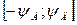называют интервал, который с заданной вероятностью 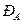, называемой доверительной, накрывает истинное значение измеряемой величины.

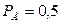– вероятностная ошибка, шансы 1:1, доверительный интервал ;

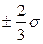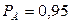– вероятностная ошибка, шансы 20:1, доверительный интервал 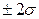; 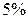погрешностей больше 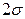, т.е. 1 замер из 20.

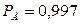–доверительный интервал 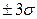– правило трех сигма практически все погрешности укладываются в этот интервал.

Другие распределения при измерениях

равномерное	двухмодальное	дискретное

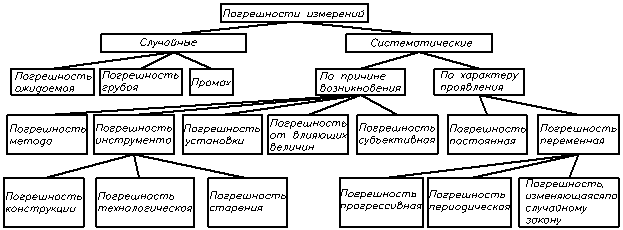
Систематическая погрешность – составляющая погрешности измерения, остающаяся постоянной или закономерно изменяющаяся при повторных измерениях. Обнаруженную и оцененную погрешность исключают из результата введением поправки.

По причине возникновения:

Погрешность метода – несовершенство принципа измерения, недостаточная изученность физического явления, на основе которого измеряют.

Инструментальная погрешность – погрешность изменяемых СИ.

Погрешность установки – неправильность установки.

Погрешность от влияния величины – тепловые и воздушные потоки, магнитные, электрические, гравитационные и др. поля, атмосферное давления, влажность, облучение.

Субъективная погрешность – неправильные навыки оператора, ошибки отсчета десятых доле по шкале и т.д.

По характеру проявления:

Постоянные погрешности – причины: неправильная градуировка, неправильная установка на 0 и т.д.

Переменные погрешности – изменяются при повторных измерениях; причины: действие внешних факторов и особенности конструкции СИ.

Эти погрешности есть и при статистических и при динамических измерениях, соответственно они будут называться статическими и динамическими.

Глава 2 Основные сведения о СИ

2.1 Классификация СИ

по виду, принципу действия и метрологическому назначению.

Виды средств измерений – мера, измерительные устройства, измерительные установки и измерительные системы.

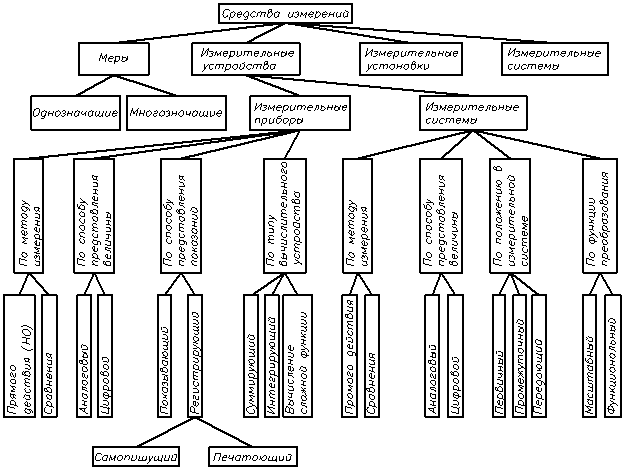
Мера – средства измерений, предназначенные для воспроизведения ФВ заданного размера.

Измерительные устройства применяются самостоятельно или в составе измерительных установок или измерительных систем. Измерительные устройства делятся на измерительные приборы и измерительные преобразователи в зависимости от формы представления сигнала.

Измерительный прибор – СИ, предназначенные для выработки сигнала измерит.: информации в форме, доступной для непосредственного восприятия наблюдателем (шкала, цифры, индикатор).

Измерительный преобразователь – СИ, предназначенные для выработки сигнала измерительной информации в форме, удобной для передачи, дальнейшего преобразования, обработки или хранения, но неподдающаяся непосредственному восприятию.

Измерительная установка – совокупность мер, измерительных приборов, измерительных преобразователей и вспомогательных устройств, предназначенных для выработки информационного сигнала в форме, удобной для восприятия и в одном месте.

Информационно-измерительная система – совокупность функционально соединенных измерительных, вычислительных и других вспомогательных технических средств, служащая либо для получения измерительной информации, обработки в целях представления потребителю (и АСУ) в требуемом виде, либо для автоматического осуществления логических функций контроля, диагностики, идентификации.

По принципу действия – какой физический принцип положен в основу построения средств измерения данного типа, указан в названии: термоэлектрический термометр, электромагнитный расходомер и т.д.

По метрологическому назначению различают образцовые и рабочие СИ, эталоны.

ОСИ – мера, измерительный прибор, измерительный преобразователь, служащие для поверки по нему рабочих СИ и образцовых меньшей точности.

РСИ – средства, применяемые для практических измерений во всех отраслях, подразделяются на СИ повышенной точности и технические.

Эталоны – служат для воспроизведения и хранения физических величин и передачи их размера через ОСИ РСИ.

2.2 Структурные схемы измерительных устройств

Любое измерительное устройство (ИУ) рассматривают как преобразователь входного сигнала Х в выходной Y /

ИУ состоит из элементов, предназначенных для выполнения определенных функций.

Преобразовательный элемент – элемент СИ, в котором происходит одно из ряда последовательных преобразований величины.

Измерительная цепь – совокупность ПЭ, обеспечивающая осуществление всех преобразований сигнала измерительной информации.

Чувствительный элемент – первый в измерительной цепи ПЭ, находящийся под непосредственным воздействием измеряемой величины.

Измерительный механизм – часть конструкции СИ, состоящая из элементов, взаимодействие которых вызывает их взаимное перемещение.

Отсчетное устройство – часть конструкции СИ, предназначенная для отсчитывания значений измеряемой величины.

Регистрирующее устройство – часть регистрирующего измерительного прибора, предназначенная для регистрации показаний.

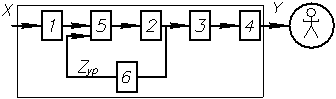
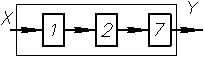
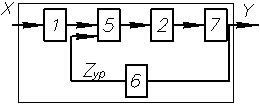
Структурные схемы измерительных устройств

а)	б)
в)	г)

а), в) – измерительный прибор прямого действия

1 – ЧЭ; 2 – ПЭ (например, усилитель); 3 – ИМ; 4 – ОУ, 7 – ПЭ, отсутствует ИМ и ОУ, без восприятия человеком, ПЭ7 формирует выходной сигнал для передачи на расстояние, для хранения, обработки.

б), г) – измерительные приборы сравнения, основаны на методе уравновешивающего преобразования ПЭ5. Обязательно наличие обратной связи. На выходе ЧЭ2 возникает сигнал 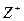и поступает в компилятор 5 (элемент сравнения двух величин, поступающих на его вход). 6 – обратный преобразовательный элемент.

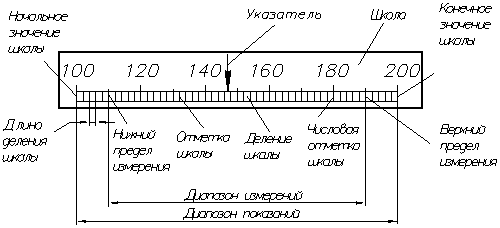
Схема отсчетного устройства измерительного прибора

2.3 Статистические характеристики и параметры измерительных устройст в

Режим работы измерительного устройства, при котором значение входного Х и выходного Y сигналов не изменяются, называют статическими (стационарными или равновесными).

Статической характеристикой измерительного устройства называется функциональная зависимость выходного сигнала от выходного в статическом режиме работы этого устройства

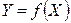
Основное требование к статической характеристике – линейная зависимость .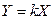

Диапазон показаний – область значений шкалы, ограниченная конечным и начальным значениями шкалы.

Диапазон измерений (рабочая часть шкалы) – область значений измеряемой величины, для которой нормированы допускаемые погрешности измерения.

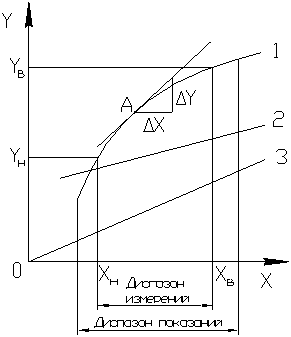Для количественной оценки влияния на выходной сигнал ИУ входного сигнала в произвольной точке статической характеристики служит предел приращения 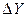к приращению входного сигнала 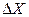, когда последнее стремится к нулю:

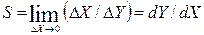
Применительно к измерительным приборам этот параметр называют чувствительностью ИУ (графически это 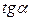). Если 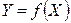нелинейная, то чувствительность 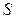будет различной в разных точках, а шкала прибора – неравномерной.

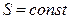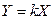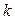Для линейной зависимости , шкала равномерная, , где – коэффициент преобразования.

Цена деления – разность двух соседних отметок шкалы. Цена деления однозначно связана с числом делений 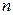шкалы ИП, в первом приближении 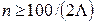, где 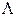– класс точности.

Порог чувствительности ИУ – наименьшее значение входного сигнала, которое вызывает заметное изменение выходного сигнала. Как правило, это полделения шкалы, поэтому порог чувствительности можно считать равным половине цены деления или классу точности .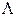

2.4 Динамические характеристики измерительных устройств

Режим работы измерительного устройства при котором значения 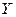и и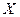зменяются во времени 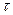, называют динамическими, или нестационарными.

Практически все ИУ имеют в своем составе инерционные элементы: подвижные механические узлы, емкости (электрические и пневматические), индуктивности и т.п.) Поэтому в динамическом режиме мгновенное значение выходного сигнала ИУ зависит не только от мгновенного значения 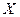, но от любых изменений этого сигнала, т.е. от его первой и второй производных (и большего порядка). Динамическая характеристика учитывает инерционные свойства ИУ.

Динамическая характеристика ИУ – это зависимость 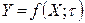в динамическом режиме.

Динамическая характеристика обычно описывается дифференциальным уравнением, передаточной или комплексной частотной функцией.

Переходные характеристики ИУ

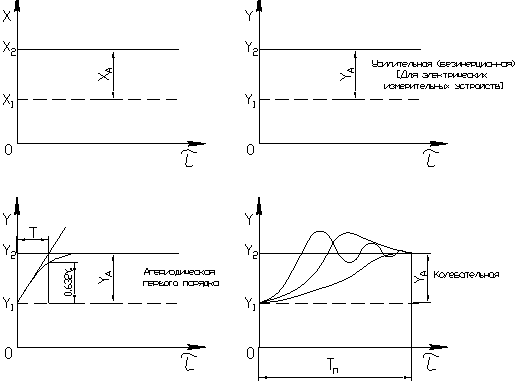
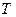– постоянная времени; 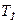– время установления выходного сигнала (время реакции); .

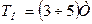2.5 Погрешности измерительных устройств

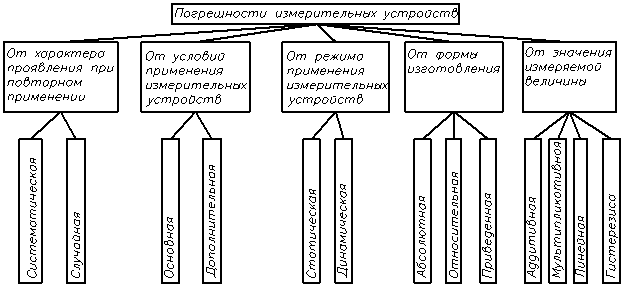
Основной погрешностью ИУ называется погрешность при использовании ИУ в нормальных условиях. Нормальные условия применения указываются в стандартах или в ТУ к ИУ.

Дополнительной погрешностью называется изменение его погрешности, вызванной отклонением одной из влияющих величин от ее нормативного значения (или нескольких).

Дополнительная погрешность добавляется к основной при применении в рабочих условиях (шире нормальных).

Абсолютная погрешность измерительного прибора ,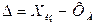

где 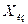– показания прибора;

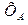– действительное значение измеряемой величины (истинное), определяется образцовым прибором или мерой.

Относительная погрешность измерительного прибора 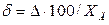. Так как 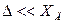или 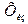, то часто используют выражение .

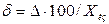Приведенной погрешностью измерительного прибора называют отношение абсолютной погрешности измерительного прибора к нормируемому значению : .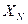

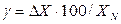В качестве нормирующего значения используется верхний предел измерений, диапазон измерений и др., т.е.

.

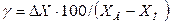Для рассмотрения зависимости погрешности ИУ от значения измеряемой величины применяют понятие номинальной и реальной функций преобразования ИУ.

Номинальной (или идеальной) функцией преобразования называют функцию, которая приписана измерительному устройству данного типа, указана в его паспорте и используется при выполнении с его помощью измерений.

Реальной функцией преобразования называют ту функцию преобразования, которой обладает конкретный экземпляр ИУ данного типа.

Реальная функция (РФ) отличается от номинальной из-за несовершенства конструкции и технологии изготовления. Эти отклонения зависят от значения измеряемой величины. По этому признаку погрешности принято разделять на аддитивную, мультипликативную, линейности и гистерезиса.

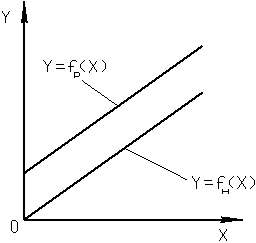
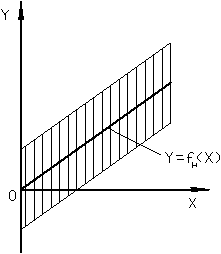
а)	б)

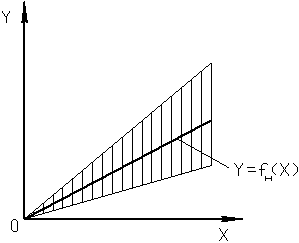
Аддитивной (получаемой путем сложения), или погрешностью нуля ИУ, называют погрешность, которая остается постоянной при всех значениях измеряемой величины. Если аддитивная погрешность является систематической, то она может быть устранена. Для этого в ИУ имеется корректор нулевого значения выходного сигнала.

Если аддитивная погрешность является случайной, то ее нельзя исключить, а реальная функция смещается по отношению к НФ произвольным образом. При этом для РФ можно определить некоторое положение (рис. б), ширина которой остается постоянной остается постоянной при всех значениях измеряемой величины.

Возникновение случайной аддитивной погрешности обычно вызвано трением в опорах, контактным сопротивлением, дрейфом нуля, шумом и фоном ИУ.

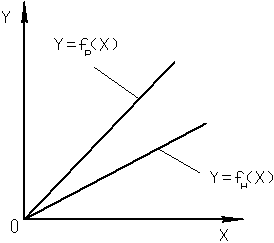
в)	г)

Мультипликативной (поучаемый путем умножения), или погрешностью чувствительности ИУ, называют погрешность, которая линейно возрастает (или убывает) с увеличением измеряемой величины. Графически появление мультипликативной погрешности интерпретируется поворотом РФ относительно НФ (г).

Если мультипликативная погрешность является случайной величиной, то реальная функция преобразования представляется полосой, как показано на рис. г. Причиной возникновения МП обычно является изменение коэффициентов преобразования отдельных элементов и узлов ИУ.

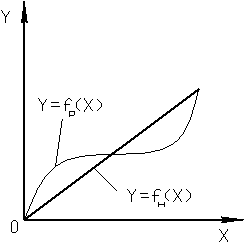
д)	е)

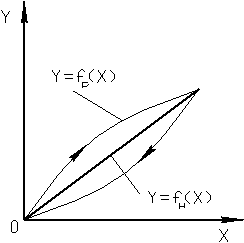
Если НФ линейна, а РФ отличается от нее так, как показано на рис. д, то такую систематическую погрешность называют погрешностью линейности.

Погрешность гистерезиса (от греч. запаздывание), или погрешность обратного хода выражается в несовпадении РФ с НФ при увеличении (прямой ход) и уменьшении (обратный ход) измеряемой величины (рис. е). Причинами гистерезиса являются: …и сухое трение в механических передающих элементах, внутреннее трение в материалах пружин, явление упругого последействия в упругих чувствительных элементах, явление поляризации в электрических, пьезоэлектрических и электрохимических элементах и др.

При случайной погрешности гистерезиса используют понятие «размах» и «вариация».

а)	б)	в)

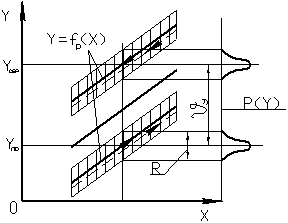
Размахом (непостоянством) 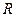выходного сигнала выходного сигнала измерительного преобразователя (показаний измерительного прибора) называют разность между наибольшим и наименьшим значениями выходного сигнала при одном значении измеряемой величины, полученными многократным односторонним подходом к этому значению, т.е. при прямом или только при обратном ходе.

Вариацией 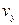выходного сигнала измерительного преобразователя (показаний измерительного прибора) называют среднюю разность между значениями выходного сигнала, соответствующая одному и тому же значению измеряемой величины, полученными при многократном и двустороннем подходе к этому значению, т.е. при прямом и обратном ходе: .

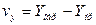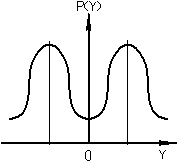
При наличии вариации закон распределения выходного сигнала ИУ является двухмодальным. Если размахи для нижней и верхней ветвей перекрываются, то закон распределения выходного сигнала имеет вид, показанный на рис б.

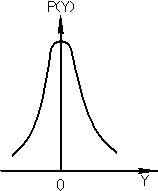
При отсутствии вариации закон распределения выходного сигнала является одномодальным или нормальным (рис. в).

2.6 Нормирование метрологических характеристик ИУ

Общий подход при нормировании метрологических характеристик состоит в том, что для всех нормируемых функций и значений устанавливаются номинальные функции и номинальные значения и пределы допустимых отклонений.

Основная погрешность ИУ нормируется путем установления предела допускаемой абсолютной, относительной или приведенной погрешности: 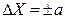; ; 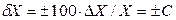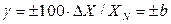, где 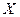– входной сигнал ИУ. Нормирующее значение 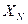– диапазон измерений, конечное значение шкалы, длина шкалы.

Способ задания пределов допускаемой основной погрешности для измерительных приборов определяется зависимостью их погрешности от значения измеряемой величины и требованиями простоты. Если погрешность ИУ является аддитивной, т.е. не зависящей от значения измеряемой величины, то предел допускаемой основной погрешности нормируется абсолютной погрешностью 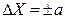, либо приведенной погрешностью .

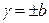Если погрешность ИУ является мультипликативной и пропорциональна значению измеряемой величины (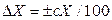), то предел допускаемой основной погрешности удобно нормировать через относительную погрешность .

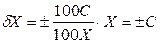Значения предела относительной или приведенной погрешности определяются из ряда перечисленных чисел:

,

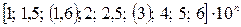где 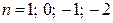; и т.д.

Допускаемые значения размаха принимается меньшим половины предела допускаемой погрешности: .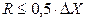

Значение предела допускаемой вариации принимается в виде кратного значения предела допускаемой основной погрешности , .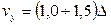

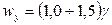Дополнительная погрешность нормируется для рабочих условий в тех случаях, когда при изменении ВФВ основная погрешность превышает установленный для нее предел. Пределы 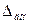устанавливаются в виде кратного значения 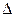, 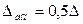(обычно).

В зависимости от степени защищенности СИ от внешних воздействий и устойчивости к механическим воздействиям ИП подразделяются на обыкновенные, виброустойчивые, пыле- и влагозащищенные, взрывобезопасные и т.д. Это дает возможность выбрать СИ применительно к данным условиям.

ИУ принято делить на классы точности.

Класс точности СИ – это обобщенная характеристика СИ, численно равная основной допустимой погрешности выраженная в процентах (приведенная и относительная).

Обозначение классов точности 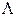производится в зависимости от способов задания пределов основной допускаемой погрешности.

Для приведенной погрешности кл. 1,5…1,5;

для относительной (обязательно в кружке)

Для технических измерений нормальные условия эксплуатации ИУ выбирают такими, что в большинстве случаев исключается необходимость нормирования дополнительной погрешности. Поэтому класс точности однозначно определяет точность этих средств измерения.

Глава 3 Результаты теплотехнических измерений и их погрешности

3.1 Теплотехнические измерения с однократными и многократными наблюдениями

Основной задачей теплотехнических измерений является формирование потока измерительной информации, необходимой для непосредственного и непрерывного контроля и управления технологическими процессами. При этом используются измерения с однократными и многократными наблюдениями. Общий подход к применению этих измерений состоит в следующем:

если систематические погрешности являются определяющими, т.е. их значения существенно больше значений случайных погрешностей, то целесообразно для определения значения измеряемой величины использовать наблюдения с однократными наблюдениями;

если случайная погрешность является определяющей, то необходимо использовать измерения с многократными наблюдениями.

Теплотехнические измерения с однократными наблюдениями применяются для контроля всех важных параметров ТПП – 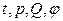. На основе этих измерений строятся автоматические системы регулирования ТПП.

(Однократные потому, что высокая скорость протекания ТПП, сложная взаимосвязь; многократные – в основном разработки математических моделей ТПП).

Измерительный эксперимент проводится по известной (типовой) или специально разработанной методике.

Методика измерений – это совокупность метода, средств, процедур и условий подготовки и проведения измерений, а также правил обработки результатов измерений.

3.2 Представление результатов измерений.

Окончательный результат измерения величины А представляют в форме 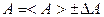. При выполнении любых измерений применяются правила округления результатов.

1) Числовое значение результата измерения должно оканчиваться десятичным знаком того же разряда, что и значение его погрешности. Большее число не имеет смысла, а меньшее увеличивает неопределенность результата.

2) Величину погрешности 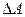необходимо округлить до 2 значащих цифр, если первая из них – единица, и до одной значащей цифры во всех остальных случаях (если двойка, то округляют до 2; 2,5, 3). При одной значащей цифре девятку (9) не применяют, например: 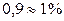, или .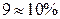

Правильная запись результата измерения температуры 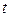при .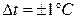

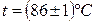3.3 Систематические погрешности и методы их определения

3.3.1 Классификация систематических погрешностей

В зависимости от источника возникновения систематические погрешности делят на инструментальные, методические и субъективные.

В зависимости от характера систематической погрешности подразделяются на обнаруживаемые и необнаруживаемые.

Обнаруживаемые систематические погрешности подразделяются на постоянные и переменные.

Постоянные возникают в основном из-за неточностей в градуировке СИ, т.е. отклонения фактической функции преобразования от номинальной.

К переменной относятся погрешности, возникающие из-за изменения внешних условий (нестабильность источников электропитания, изменение 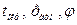, действия внешних полей и т.д.)

Необнаруживаемые систематические погрешности могут быть предсказаны либо выявлены при обработке результатов измерений. Причина – неучтенные методические погрешности, субъективные ошибки, недостаточная информация о характеристиках средств измерений.

3.3.2 Методы определения и уменьшения систематических погрешностей

1. Определение постоянных погрешностей.

Постоянные погрешности характеризуются функцией преобразования, или градуировочной характеристикой. Если СИ исправно, то при нормальных условиях эксплуатации не должна выходить за установленные границы. СИ подвергается периодическому контролю и признается годным (или непригодным). В некоторых случаях их подвергают индивидуальным градуировкам (тарированию). Индивидуальная градуировка оформляется в виде таблиц, графиков или аналитическим функциям.

Пределы допустимых погрешностей СИ (паспортные или индивидуальные) должны рассматриваться как границы неисключенной систематической погрешности.

2. Определение и уменьшение переменных погрешностей.

Переменные погрешности возникают из-за изменения внешних условий. Для определения всех составляющих переменных погрешностей проводят специальные эксперименты, в которых поочередно меняют каждую из влияющих величин в заданных пределах. Это дополнительные погрешности, их относят к определенному диапазону измерений ВФВ (например, дополнительная приведенная погрешность не превышает 0,2 % на каждые 10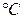измерения окружающей температуры .

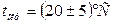Уменьшить переменную погрешность можно, устраняя и уменьшая изменение внешних условий. Для этого используют стабилизацию питания, термостабилизацию, экранирование от внешних полей, амортизацию и другие методы.

Пределы неустраненных переменных погрешностей должны рассматриваться как границы дополнительной неисключенной погрешности.

3. Влияние и уменьшение необнаруживаемых погрешностей

Единственным путем выявления необнаруживаемых систематических погрешностей является проведение измерений двумя или несколькими независимыми методами, обладающими приблизительно одинаковыми постоянными и переменными систематическими погрешностями. При нескольких методах измерений сравнивают их результаты, и отбрасывают те из них, которые грубо отличаются от остальных. По оставшимся находят 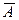и вероятностную ошибку как при расчете случайной погрешности.

Или применяют более точный метод.

3.4 Случайные погрешности и методы их определения

Случайные погрешности могут быть определены, если результаты получаются на основании многократных измерений величины, значение которой не изменяется в течение всего процесса измерений.

При числе наблюдений 20 и более распределение случайных величин происходит по нормальному закону, а при числе наблюдений менее 20 – распределению Стьюдента.

3.4.1 Определение грубых ошибок

Грубые ошибки определяют на основании обработки результатов наблюдений. Пусть выполнено 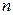наблюдений, тогда среднее арифметическое значение результатов наблюдения находят по формуле

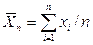, где 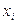– результаты наблюдений.

Среднее квадратическое отклонение ряда измерений определяется по формуле:

.

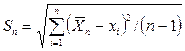Для обнаружения грубых погрешностей используется ряд критериев (критерий 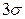, Шовинэ, Романовского, Грейса).

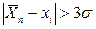
Результаты наблюдений с грубыми погрешностями исключаются из дальнейших расчетов, и снова находится среднее арифметическо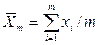е , где 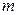– число наблюдений после исключения грубых ошибок, а также .

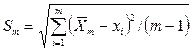3.4.2 Определение доверительных границ случайных погрешностей измерения

Для определения доверительных границ погрешности измерения доверительную вероятность принимают равной .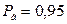

Сначала находят среднеквадратическое отклонение среднего арифметического

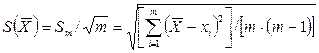
Для интервальной оценки используют распределение Стьюдента (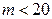), или 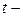распределение. Границы доверительного интервала ,

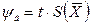где 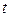– коэффициент распределения Стьюдента, зависящий от заданной 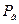и числа степеней свободы 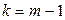для .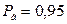

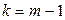
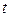
	12,7	4,3	3,18	3,78	2,57	2,45	2,37	2,31	2,26

при .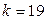

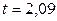3.5 Нахождение результатов измерений

Рассмотрим методы нахождения результатов прямых и косвенных измерений при одно- и многократных наблюдениях.

1) Простейший случай – прямое измерение с однократным наблюдением

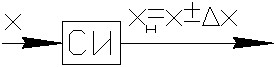
Результат измерения 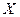есть наблюдаемое значение ().

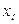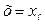2) Прямое измерение с многократными наблюдениями

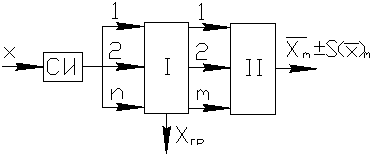
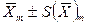– результат измерения

, ,

, , ,

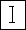
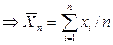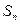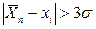
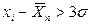
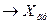
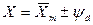
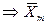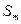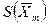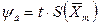
3) Косвенное измерение – состоит в том, что измеряемую величину находят расчетом по определенным формулам, в которые входят результаты прямых измерений двух или нескольких величин (например, для измерения холодопроизводительности компрессора необходимо измерить температуру, расход, давление, которые затем подставляются в соответствующую формулу).

Для выполнения измерения необходимо знать статическую связь между конечной косвенно измеряемой величиной 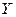входящими в нее величинами 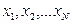, измеряемыми при помощи СИ₁, СИ₂, … СИ_N.

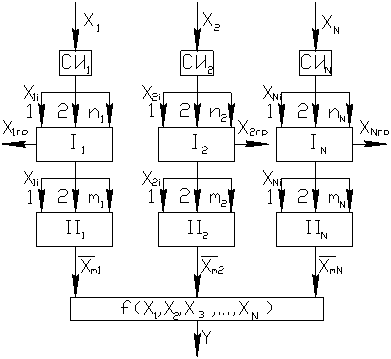
косвенные измерения с однократными наблюдениями	косвенные измерения с многократными наблюдениями

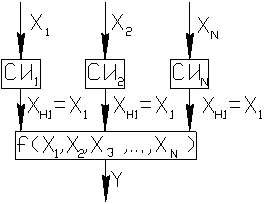
Пусть эта связь представляет собой функцию .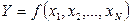

При однократных наблюдениях каждой величины результаты измерений совпадают с результатами наблюдений , , … .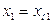

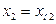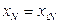Эти величины подставляются в функцию 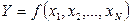. Результат вычислений является результатом косвенного измерения.

Схема косвенного измерения с многократными наблюдениями: 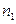– число наблюдений величины , – , … – .

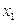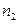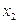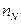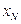Операциями 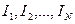отфильтровывают результаты наблюдений с грубыми ошибками 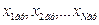, после чего остаются 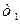наблюдений величины 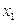, 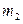– величины 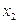, и т.д., 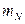– величины 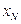. Эти результаты наблюдений проходят операции 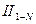по нахождению среднего арифметического значения 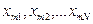, которые являются результатами измерений исходных величин. Полученные результаты вводятся в функцию 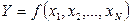, после вычисления которой получают результат косвенного измерения.

3.6 Вычисление суммарных погрешностей

3.6.1 Составляющие суммарных погрешностей

В зависимости от числа проводимых наблюдений и методики их обработки в расчет суммарной погрешности могут вводится следующие составляющие.

При однократных наблюдениях, а также небольшом числе наблюдений, не подвергающихся статистической обработке, в расчет вводят неисключенную систематическую погрешность, которая включает в себя инструментальную, методическую и субъективную составляющие.

Инструментальная погрешность определяется через пределы допускаемых основных и дополнительных погрешностей средств измерений, которые указываются в технических характеристиках или в данных индивидуальной градуировки. Методическая погрешность выявляется анализом методики измерения или соответственно, экспериментом. Субъективная погрешность может быть учтена лишь условно. Например, при отсчете показаний стрелочных приборов субъективную погрешность можно принимать в размере 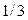минимального деления шкалы.

При многократных наблюдениях в расчет вводят неисключенную систематическую погрешность и доверительной границы случайной погрешности, найденные на основании статистической обработки результатов наблюдений.

3.6.2 Вычисление суммарных погрешности при однократных наблюдениях

При нахождении суммарной погрешности все составляющие рассматриваются как случайные величины с равномерным распределением. Границы суммарной погрешности, которые в данном случае совпадают с границами неисключенной систематической погрешности, т.е. 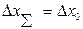и 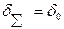, рекомендуется вычислять по приведенным формулам:

в относительной форме 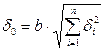; (а)

в абсолютной форме ,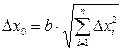

где 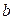– коэффициент, который при 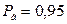принимают равным 1,1; 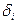– граница 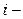ой неисключенной систематической погрешности (в относительной форме); 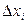– граница 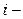ой неисключенной систематической погрешности (в абсолютной форме); 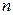– количество учитываемых составляющих.

Прямое измерение. Если прямое измерение выполняется одним средством измерения, границу суммарной относительной погрешности измерения вычисляют по формуле (а), которая приобретает вид

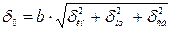(в)

где 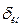, , 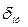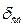– границы относительных погрешностей: инструментальной, методической и субъективной.

Если паспортная инструментальная погрешность СИ задана в виде абсолютной погрешности, то величина 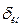определяется по формуле

,

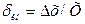где 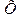– результат измерений при нескольких измерениях .

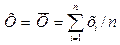Если паспортная инструментальная погрешность СИ задана в виде приведенной относительной погрешности (или класса точности), то величину 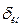определяют по формуле:

,

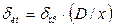где 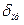– приведенная относительная погрешность (класс точности);

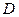– нормированная величина (обычно диапазон измерений).

Методическая и субъективная погрешность (относительная и абсолютная) вычисляются аналогично.

Граница суммарной погрешности в абсолютной форме:

.

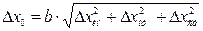Часто измерение производится не одним, а несколькими средствами, соединенными последовательно в измерительную цепь (например, измерение температуры с помощью последовательно соединенных термопреобразователя сопротивления, передающего нормирующего преобразователя и показывающего миллиамперметра). При этом каждое из средств измерений характеризуется собственной паспортной инструментальной погрешностью. Каждая из границ инструментальной погрешности должна быть приведена к общему виду по формулам для 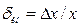или 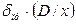, причем в качестве результата измерений следует принимать соответствующее значение выходной величины каждого средства измерения. Например, для термопреобразователя сопротивления выходной величиной является величина электрического сопротивления, для нормирующего преобразователя – выходной ток и т.д. После указанной операции находится величина

,

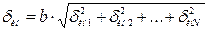где 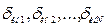– границы относительной инструментальной погрешности средств измерений от 1-го до 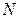-го, входящих в измерительную цепь.

Расчет границ суммарной погрешности производят по формуле (в) с подстановкой в нее значения 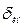. Методическая и субъективная составляющие при этом остаются теми же, что и в случае измерения одним СИ.

Определение суммарной погрешности измерительной цепи через абсолютные погрешности относительно СИ в данном случае невозможно, т.к. каждая из этих величин может выражаться в разных единицах.

Косвенное измерение: .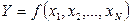

Косвенное измерение предполагает наличие расчетной формулы, связывающей результаты прямых измерений отдельных составляющих величин с косвенно измеряемой величиной:

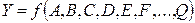или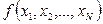

Среди переменных 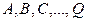могут быть величины трех типов:

1) величины, определяемые путем прямых измерений (например, велич

Дата добавления: 2013-12-11