Теорема взаимности

Входные и взаимные проводимости ветвей

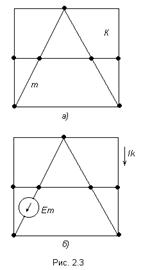
На рис. 2.3а изображена скелетная схема пассивной цепи. В каждой её ветви есть сопротивление. Выделим две схемы ветви m и k. Поместим в ветвь m Э.Д.С. (рис 2.3б). Выберем контуры в схеме так, чтобы k- ветвь входила только в k- контур, а m- ветвь, только в m-контур. Э.Д.С. E_m вызовет точки в ветвях m и k.

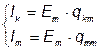
Коэффициенты q имеют размерность проводимости. Коэффициент q_mm называют входной проводимостью ветви m, q_km – взаимной проводимостью.

Для расчёта проводимостей составляют уравнения по методу контурных токов, следя за тем, чтобы ветви, взаимные и входные проводимости которых представляют интерес, входили каждая только в свой контур. Далее находят определитель системы ∆ и по нему необходимые алгебраические дополнения. Вычисляем проводимости по формуле 2.2:

; .

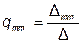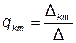Теорема взаимности формируется таким образом: для любой линейной цепи с одним источником Э.Д.С. ток I_k в ветвях, вызванный Э.Д.С. E_m, находящийся в m-ветви, будет равен току I_m в m-ветви, вызванному Э.Д.С. E_k (численно равной E_m) находящейся в k ветви.

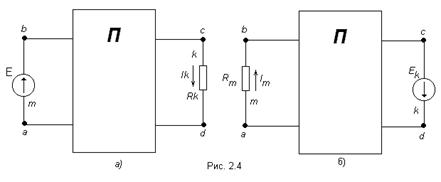
Другими словами, сущность принципа взаимности состоит в следующем. Пусть имеется электрическая схема произвольной конфигурации с единственным источником Э.Д.С. E_m, который действует в m-ветви в направлении от точки а к точке в (рис 2.4а) и создаёт в k-ветви с сопротивлением R_k ток I_k, направленный от точки с к точке d. Такой же источник Э.Д.С. E_k = E_m, включенный в k-ветвь и действующий от точки c к точке d (рис 2.4б) создаёт в m-ветви с сопротивлением R_m = R_k ток I_m, направленный от точки а к точке b и равный току I_k.

На рис. 2.4 пассивным четырёхполюсником (прямоугольником с буквой П) обозначена вся остальная часть схемы, не содержащая источников Э.Д.С. и источников тока.

Токи в ветвях m и k.

;

.

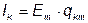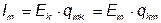Можно отметить, что теорема взаимности справедлива не только для токов, но и для напряжений.

· Для нелинейных цепей теорема взаимности невыполнима.

· Теорема взаимности справедлива лишь для тех линейных электрических цепей, которые содержат один источник Э.Д.С.

ПРИМЕР:

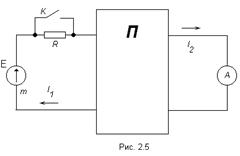При замкнутом ключе К в цепи источника протекает ток, равный 5А, а ток через амперметр равен 6 мА. Е=100 В R=5 Ом. Как изменятся эти токи, если ключ разомкнуть?

РЕШЕНИЕ:

Определим входное сопротивление четырёхполюсника:

.

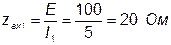После размыкания ключа К ток в цепи источника будет равен:

.

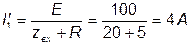Для нахождения тока 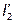после размыкания ключа воспользуемся принципом взаимности, согласно которому источник Э.Д.С. Е и амперметр можно поменять местами. Схема приобретёт следующий вид:

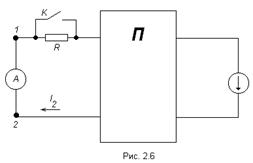Если ключ К замкнут, то .

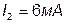Если амперметр убрать из схемы, то можно определить напряжение холостого хода на зажимах 1-2 (такой приём называется методом холостого хода и короткого замыкания, которые обычно используются для определения входного сопротивления).

.

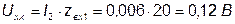После размыкания ключа ток, протекающий через амперметр, будет равен:

.

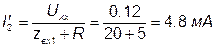ОТВЕТ: .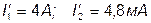

Дата добавления: 2013-12-11