Общие понятия

Лекция 9. Дифференциальное уравнение

Формула парабол

Еще более точной при прочих одинаковых условиях является формула парабол (формула Симпсона)

(8.14)

В основу ее вывода положена идея замены каждой части дуги кривой , проходящей через три фиксированных соседних точек, дугой параболы , проходящей через эти же точки.

При использовании формулы парабол отрезок интегрирования следует разделить точками на четное число равных частей.

Существуют и другие методы приближенного интегрирования, а также оценки погрешностей результатов приближенных вычислений по сравнению с точными значениями.

Обыкновенным дифференциальным уравнением называется уравнение, связывающее независимую переменную , неизвестную функцию 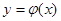и ее производные или дифференциалы различных порядков.

Общий вид дифференциального уравнения

(9.1)

или (9.2)

Напомним, что производные можно выразить через отношение дифференциалов (9.3)

Обыкновенные дифференциальные уравнения бывают первого, второго и т.д., 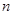-ого порядка. Порядок уравнения определяется порядком старшей производной, входящей в это уравнение. Например:

- уравнение 1-ого порядка,

- уравнение 2-ого порядка,

- уравнение 3-его порядка.

Кроме обыкновенных дифференциальных уравнений бывают еще дифференциальные уравнения в частных производных, связывающие несколько независимых переменных, неизвестную функцию этих переменных и частные производные этой функции разных порядков. Таких уравнений мы касаться не будем.

Решением дифференциального уравнения (9.1) называется любая функция 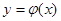, удовлетворяющая этому уравнению, то есть обращающая его в тождество при подстановке этой функции и ее производных в дифференциальное уравнение.

Например, решением уравнения 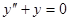будет функция . Ее вторая производная 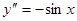. Если подставить в данное уравнение, получим .

Еще пример. Пусть дано простейшее дифференциальное уравнение первого порядка или Интегрируя обе части этого уравнения, найдем . Отсюда видно, что решением дифференциального уравнения будет не одна, а множество функций, отличающихся произвольной постоянной величиной С.

Рассмотрим простейшее дифференциальное уравнение второго порядка или , или . Интегрируя обе части этого уравнения, найдем 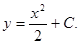Отсюда видно, что решением дифференциального уравнения будет не одна, а множество функций, отличающихся произвольной постоянной величиной С.

Рассмотрим простейшее дифференциальное уравнение второго порядка

. Запишем его так , . Интегрируя получим или , откуда . Интегрируя еще раз найдем . Откуда видим, что решение уравнения 2-го порядка содержит две произвольные постоянные 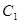и .

Решения дифференциальных уравнений, как только что было показано, получаются в результате интегрирования неких дифференциалов. Поэтому решение называют еще интегралом дифференциального уравнения.

Общим решением дифференциального уравнения 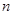-го порядка (9.1) называется его решение, полученное после 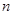последовательных интегрирований и выраженное в виде явной функции от независимой переменной , содержащей 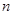независимых произвольных постоянных , ,

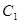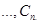
(9.4)

Общим интегралом дифференциального уравнения 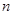-го порядка называется его решение, выраженное в виде неявной функции

Ф (9.5)

Частным решением дифференциального уравнения 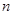-го порядка называется его решением, полученное из общего решения, в котором всем произвольным постоянным даны конкретные числовые значения. Аналогично определяется и частный интеграл.

Общему решению (интегралу) соответствует семейство интегральных кривых, частному решению (интегралу) соответствует одна определенная кривая этого семейства.

Для получения частн6ого решения из общего, надо задать начальные условия:, , 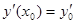,…,. (9.6)

Число начальных условий должно быть равным порядку уравнения. Начальные условия математически отражают начальное состояние процесса.

Задача о нахождении частного решения дифференциального уравнения при заданных начальных условиях называется задачей Коши (О. Л. Коши (1789-1857) – французский математик).

Дата добавления: 2013-12-12